波动方程叠前偏移成像技术应用于页岩气地震勘探

波动方程偏移以波动方程的数值解法为基础，通过递归波场延拓进行成像，波动方程类偏移方法可分为基于单平方根（SSR）单程波动方程的共炮集偏移、基于双平方根（DSR）单程波动方程的炮检距域偏移以及基于双程波动方程的逆时偏移。这三种波动方程偏移的波场延拓算子都是由标量波动方程推导出来的。

1.SSR单程波偏移

SSR波动方程偏移采用以标量波动方程因式分解得到的上、下行波方程为基础：

式中，U为上行波，代表由地表向地下延拓的接收波场；D为下行波，代表震源波场。对于不同频率分量的上、下行波场，沿深度方向逐层进行延拓，然后在地下成像点对延拓波场利用成像条件提取成像值（如图3—28、图3—29所示）。

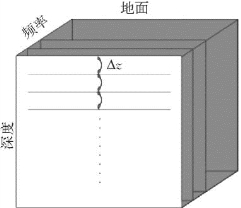
图3—28　SSR单程波偏移示意图

SSR波动方程偏移算法有很多种，主要分为以下几类：① 有限差分偏移，分为显式有限差分算法和隐式有限差分算法；② 频率—波数域偏移及相移偏移；③ 空间—波数双域算法，包括裂步傅里叶（SSF）偏移、傅里叶有限差分（FFD）偏移、广义屏（GSP）偏移等。一般来说，SSR波动方程的成像精度高于Kirchhoff偏移，但是计算效率相对较低，且存在两个固有缺陷：一方面，单程波偏移难以对倾角大于90°的陡倾地层进行成像；另一方面，单程波偏移难以用于真振幅成像。为此，国内外学者提出了相应的解决方法。针对陡倾地层成像问题，有人利用相移法偏移首先进行向下延拓，并保存每层近似平行传播的能量，然后再由下至上延拓以实现陡倾地层的成像。此外，倾斜坐标系下的波场延拓方法也可以在一定程度上解决上述问题。针对真振幅成像问题，基于更为准确的上、下行波方程，后人提出了真振幅单程波方程偏移方法，如利用反褶积成像条件可以得到真振幅的炮域共成像点道集，利用互相关成像条件则可以得到真振幅的角度域共成像点道集。

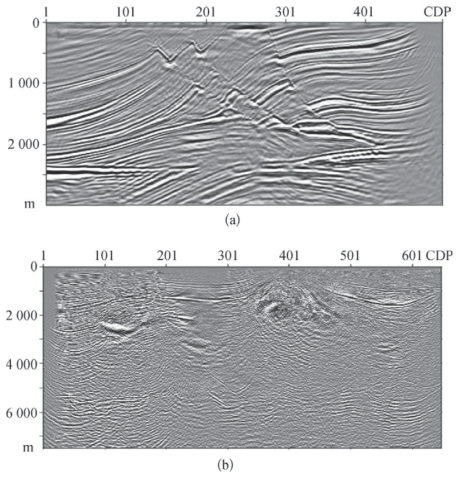
图3—29　（a）Marmousi模型与（b）N区实际资料的SSR叠前深度偏移结果(www.xing528.com)

2.DSR单程波偏移

基于DSR算子的炮检距域偏移采用“沉降观测”的成像概念，将炮点和接收点波场交替延拓，然后提取零炮检距、零时刻波场作为成像值，由DSR波动方程（式3—43）作为传播算子（如图3—30、图3—31所示）。

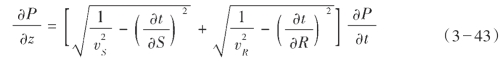
式中，S和R分别为炮点、接收点坐标矢量；S和R分别为炮点、接收点的介质速度。

图3—30　DSR单程波偏移示意图

图3—31　（a）Marmousi模型与（b）B区实际资料的DSR叠前深度偏移结果

DSR偏移理论是由Ylimaz等建立起来的。为了处理横向变速问题，Popovici把裂步傅里叶算子引入DSR方程偏移中，提出了中点—半炮检距坐标系下的DSR方程叠前深度偏移方法。随后，有人将广义屏波场延拓算子应用于DSR方程叠前偏移成像中。由于三维DSR方程全偏移的波场延拓过程是在五维空间上进行的，对计算机内存要求很高，而且计算量非常大。为解决上述问题，出现了专门针对具有某种特征三维“限定数据体”的DSR方程偏移方法，如Biondi等提出的共方位角DSR偏移技术及随后有人提出的窄方位角DSR偏移技术。