同时间偏移相比,深度偏移可以对地下地质构造进行更为精确的成像。自20世纪90年代在墨西哥湾的成像实验取得巨大成功之后,叠前深度偏移引起了地球物理界的广泛重视,并很快在全球范围内得到了推广应用。深度偏移方法在过去的几十年里得到了快速发展,并产生了许多具有各自优势的成像算法,主要可以分为射线类偏移方法以及波动方程偏移方法两大类。下面介绍几种应用较为广泛的叠前深度偏移方法,并以经典的Marmousi速度模型(如图3—23所示)为例来对比各方法的成像效果。
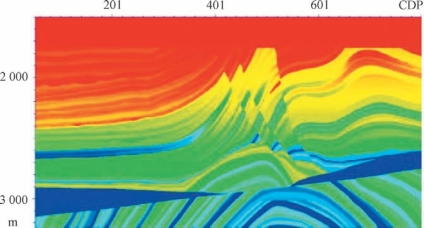
图3—23 经典Marmousi速度模型
1.Kirchhoff偏移
Kirchhoff偏移是最常用的射线类偏移方法,源于20世纪60年代的绕射扫描叠加方法,利用波动方程的Kirchhoff积分解来实现地震波场的反向传播及成像。自20世纪80年代以来,人们对Kirchhoff偏移进行了广泛的研究,衍生出一系列真振幅偏移算法以及与之相关的地震波走时算法,并因其灵活、高效的特点,在西方工业界得到了广泛应用。
Kirchhoff偏移的理论出发点是地震记录的加权绕射叠加,如共炮集Kirchhoff积分偏移可以表示为
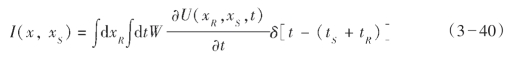
式中,x,xS,xR分别为成像点、炮点以及接收点位置;U(xR,xS,t)为接收波场,其中tS,tR分别为震源和接收点到成像点的走时;W为加权函数;δ[]为狄拉克函数;单炮成像值I(x,xS)为所有道成像贡献的叠加。
由式(3—40)不难看出Kirchhoff偏移的灵活性。首先,可以任意选定成像点位置波,因而可以很容易地实现局部目标的成像;其次,可以任意选定成像输入道,也就是说可以任意定义对应地下成像点的偏移孔径;再次,如果走时是通过射线追踪来求取,那么便可以通过控制地下射线的角度信息选定参与成像的数据采样;最后,还可以利用上述角度信息计算地下的偏移张角以及地质构造的倾角。除了上述特点之外,Kirchhoff偏移还具有很高的计算效率以及对观测系统的良好适应性,可以适应复杂的地表条件以及不规则的观测系统(如图3—24所示)。
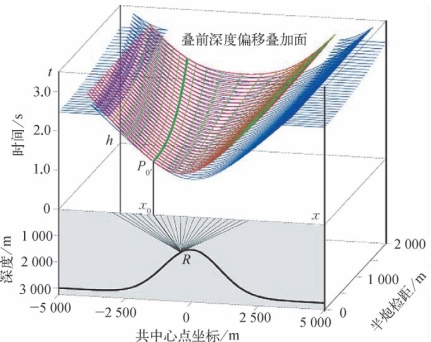
图3—24 Kirchhoff叠前深度偏移原理
由于Kirchhoff偏移依赖于地震射线方法计算地震波的旅行时间,因此也存在缺陷,表现为:一方面,常规的射线方法存在射线的焦散区及阴影区,使得由射线振幅参数表示的真振幅加权函数的可靠性大打折扣;另一方面,若地下介质复杂,则在震源、接收点和地下成像点之间往往存在多次波至。现今大部分Kirchhoff偏移算法只选择其中的单次波至(最小走时或最大振幅),单次波至往往难以对复杂构造进行有效成像,由此引起的偏移算子的截断会造成大量的偏移噪声。虽然基于多值走时的Kirchhoff偏移算法可明显提高成像质量,但会造成计算效率明显降低,且编程计算的复杂性大大提高。图3—25为Marmousi模型和M探区实际资料的Kirchhoff叠前深度偏移结果。

图3—25 (a)Marmousi模型与(b)M探区实际资料的Kirchhoff叠前深度偏移结果(https://www.xing528.com)
2.束偏移
作为射线类偏移方法的另一个分支,束偏移是一种改进的Kirchhoff偏移方法,不但可以对多次波至进行成像,而且往往具有潜在的效率优势。
Hill和Sun等奠定了此类方法的理论基础,此后一系列衍生的束偏移方法得以出现。束偏移的基本实现过程大致可以分为三步:
(1)将地震数据划分为一系列局部的区域;
(2)利用倾斜叠加,将局部区域内的地震记录分解为不同方向的平面波(也就是束);
(3)利用射线走时和振幅将平面波进行映射成像。
由于不同方向平面波的映射成像过程是相互独立的,因此束偏移可以自然地对多次波至进行成像,其成像效果往往优于常规的基于单值走时的Kirchhoff偏移。此外,束偏移往往还具有Kirchhoff偏移的高效性和灵活性,并且适用于复杂的地表条件。
作为积分法偏移的改进,高斯束偏移所使用的格林函数是一系列高斯束的叠加,每条高斯束代表地下的局部波场且处处正则,从而可以自然地对多次波至进行成像,且不存在波场的奇异性区域,其成像精度优于常规的Kirchhoff偏移,并且接近于波动方程偏移(如图3—26所示)。高斯束偏移最早由Hill提出,其基本思想为将相邻的输入道进行局部倾斜叠加,并分解为局部平面波,然后通过高斯束将局部平面波分量反传至地下局部的成像区域进行成像。由于对应每条高斯束的成像过程是相互独立的,因而可以自然地实现多次波至的成像。直接将叠后高斯束偏移的思想应用于叠前,计算效率往往较低,Hill成功地解决了上述计算效率问题,提出了适用于共炮检距、共方位角数据的叠前高斯束偏移方法。随后,Gray等对上述方法进行了拓展,将高斯束偏移用于共炮集、真振幅以及各向异性介质的偏移成像,不但适用于不同道集的叠前数据以及复杂的地表条件,还可以用于弹性波多分量叠前资料的偏移成像处理,并能够抽取不同类型的成像道集进行偏移速度分析。高斯束偏移具有较高的计算效率和成像精度,尤其适用于三维深度域偏移成像,并作为一种三维迭代速度建模的有效工具。
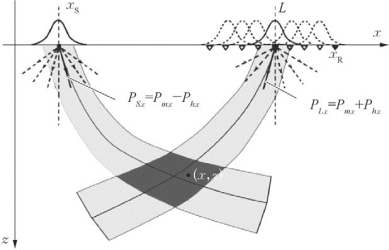
图3—26 高斯束偏移示意图
此外,CGG Vertitas公司提出控制束叠前深度偏移方法,与高斯束偏移需对τ—p域内每一个采样点进行偏移不同,控制束偏移只需对τ—p域内满足假定条件的采样点进行偏移(如图3—27所示)。
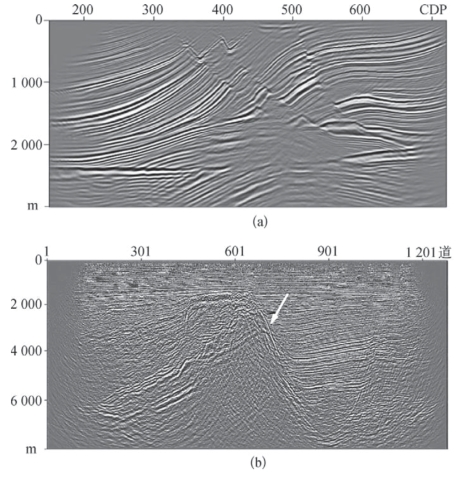
图3—27 (a)Marmousi模型与(b)中国东部S区实际资料的高斯束叠前深度偏移结果
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




