地震波传播机制与页岩气勘探技术

1.地震波的形成与实质

要了解地震波的形成过程，不妨先回顾一个常见的生活实例。如果把一块石子投入平静的水池，就会在水面上以落石点为中心形成圆环状波纹，并且逐渐向外传播出去，这种行进中的扰动就是水面波。如果细心地观察浮在水面上的一块小木块，就会发现，当波通过时，木块只是近似地上下浮动，并不随波前进。可见受到石子外力作用时，由于重力和液体表面张力的作用，落石处部分水滴首先开始振动，同时又使其相邻部分水滴相继振动，并依次将振动往外传播出去，这就是水面波动形成的过程，水面波通过水介质传播，但水滴并不随扰动前进。

在目前的地震勘探中，激发波动的“石子”一般是炸药，传播波动的是地层介质。用炸药爆炸方式激发地震波的机理虽尚未完全被揭示，但已经可以将爆炸时形成地震波的物理过程做一个初步的说明。

当炸药爆炸时，产生大量高温高压气体，并迅速膨胀形成冲击波，以上万个大气压的巨大压力作用于周围岩石。这个作用力是个瞬间起作用的脉冲力。在其作用下，靠近震源附近的岩石因所受压力远超过抗压强度而被破坏，形成一个球形破坏圈。圈内岩石质点具有很大的永久位移，常形成以震源为中心的空穴。爆炸产生的部分能量在压碎岩石和发热过程中消耗掉。随着离震源中心的距离 r 的增大，爆炸能量将传递给越来越多的岩石和地质单元，因而冲击波能量密度随着波的传播而迅速衰减，以致岩石所受压力小于其抗压强度，但仍超过岩石弹性限度，使岩石质点仍产生一定的永久位移，从而形成塑性形变（辐射状及环状裂隙），这个区间叫塑性形变带，如图3—1（a）所示。

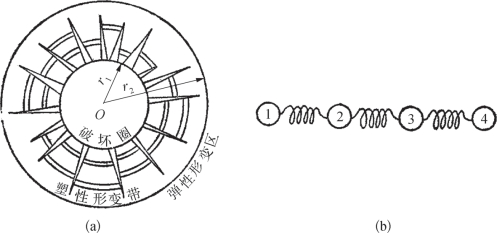
图3—1　（a）爆炸对岩石的影响；（b）弹性介质简图

在塑性带以外，随着传播距离 r 的继续增大，冲击波的能量密度继续明显衰减，使岩石所受压力降低到弹性限度之内，形变和应力很小，作用时间又很短促，岩石就具有完全弹性体的性质，其质点受激而产生弹性位移（形变），同时也就发生与之对抗的应力，使质点产生反向位移，从而使质点在平衡位置附近形成弹性振动。在塑性带外面的区域就是所谓的弹性形变区。在本区内，由于岩石具有连续结构，各质点之间存在弹性联系，使弹性介质的作用好像是一种用弹簧连接起来的质点组成的阵列，如图3—1（b）所示，每个质点在各自平衡位置上作弹性振动，而且离震源［即图3—1（a）及图3—2（a）中的O点］不同距离的质点依次先后产生这种振动。

2.地震波的动力学特点

弹性波动力学问题主要是研究波动的能量问题，这实际上就需要对波动的形状和强度变化、周期大小与激发状态和介质条件的关系作全面的研究。因此，研究波的动力学问题就成为地震勘探中的一个基本问题。

1）地震波的描述——振动图和波剖面图

地震波的振动特征和传播过程，可以通过数学物理的方法和图形的方法等来进行描述。由于数学物理方法需要做较多的数学推演，在实际工作中则常用一些比较直观的、简便的图形方法来描述。现就几种常用的描述地震波的方法和有关概念介绍如下。

（1）振动图

当地震波从爆炸点开始向各个方向传播，利用检波器和地震仪记录由于地震波的到达而引起地面质点的振动情况，就得到地震记录，其中某一条曲线就是波到达某一检波点的振动图。因此，振动图又叫地震记录道。

如图3—2所示，假设在离震源距离为r1的A点观测质点振动位移随时间的变化规律，用时间 t 为横坐标，质点位移u为纵坐标作图，可得到图3—2（b）所示的图形，从图中可看出该点地震波振动的位移大小（称之为振幅值变化）、振动周期（T）、延续时间（Δt）等特征。这种用（u，t）坐标系统表示的质点振动位移随时间变化的图形称为地震波的振动图。在实际地震记录中，每一道记录就是一个观测点的地震波振动图。

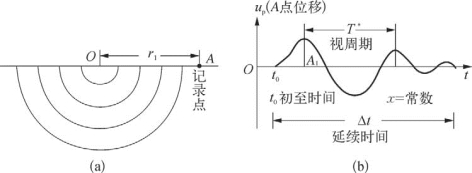
图3—2　振动

地震勘探中，地震波从激发到地面接收到反射波，最长时间只有6 s左右，波在传播中振幅也是可变的。这种延续时间短，振幅可变的振动区别于普通物理学中所讲的周期振动，称为非周期脉冲振动。

对非周期振动可用视振幅、视周期和视频率来描述它。

视振幅即质点离开它平衡位置的最大位移。如图3—2（b）中的A1，振幅大表示振动能量强，振幅小表示振动能量弱，因为根据波动理论，可以证明振动能量的强弱与振幅的平方成正比。

视周期即两个相邻极大点或极小点之间的时间间隔，用T*表示，它说明质点完成一次振动所需要的时间。

视频率即表示质点每秒内振动的次数，用f *表示。T*与f *互为倒数，即f *＝1/T*。

（2）波剖面图

振动图只反映了地面某一质点的振动情况，而波剖面图则反映了波在传播过程中，在某一时刻整个介质振动分布的情况。如图3—3（a）所示，假设在某一确定的时刻 t，在距离震源点O的一定范围内的各不同距离的点上，同时观测它们质点振动的情况，并以观测点与震源O的距离x为横坐标，以质点离开平衡位置的位移u为纵坐标作图，所得图形如图3—3（b）所示，从图中可以看出质点振动的波长λ和该时刻的起振点x2（波前）及停振点x1（波尾）等特征。这种描述某一时刻t质点振动位移u随距离x变化的图形称之为波剖面图。

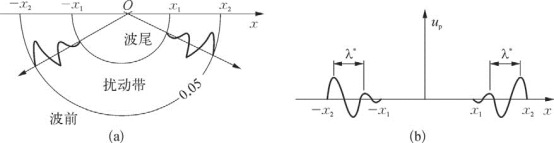
图3—3　波剖面图

假设地下是均匀介质（即波速＝常数），在O点爆炸后，地震波就从这一时刻向各方向传播。如果某一时刻tK所有刚开始振动的点连成曲面，这个曲面叫作该时刻tK的波前；而由tK时刻所有逐渐停止振动的各点连成的曲面，叫作tK的波尾（或波后），如图3—3（a）所示。波前表示某一时刻地震波传播的最前位置。根据波前的形状，可以把波区分为球面波和平面波。

为了把在某一时刻tK波在整个介质中的振动分布情况表示出来，用横坐标x表示通过震源O的直线上各个质点的平衡位置，纵坐标u表示在tK时刻各个质点的位移。将各质点位移连成曲线，所得到的图形即为波剖面，如图3—3（b）所示。

在波剖面图中，最大的正位移的点叫作波峰，最大的负位移的点叫作波谷。两个相邻波峰或波谷之间的距离叫作视波长，以λ*表示 （即在一个周期内波前进的距离）。波长的倒数叫作视波数k*。波前和波后以速度*向外扩大，在一个周期内，沿x方向传播的距离是一个波长，所以

根据上述讨论，地震波的振动图和波剖面图与震源及传播介质的性质密切相关，而当震源和传播介质一定时，振动位移u是时间t和观测位置x的函数，即u＝u（t，x）。若固定一个变量来研究u随另一个变量的变化关系，则分别称为振动图和波剖面图。这两个图形之间有密切的联系，只是从不同的角度来观察而已，在图3—3中以简谐振动为例表示出了波剖面图和振动图之间的关系。

2）地震波的频谱及其分析

前面谈到质点的振动，只经过一个短暂时间Δt振动之后就逐渐停止下来，这种现象表明，由爆炸所引起的质点振动是一种非周期性的瞬时振动即脉冲振动。根据振动的数学理论（傅里叶变换—傅里叶级数）可证明：脉冲地震波这样一个复杂非周期性瞬时振动，可以看作是无限多个不同频率、不同相位、不同振幅的谐和振动的复合振动。其中任何一个振动都可表示为：

式中，u（t）是质点在任一时刻t的位移，A是质点位移振幅（即最大位移值），f是振动频率（即自然频率），φ是决定t＝0时刻质点位移值的初相位。

如图3—4所示，三个频率、相位与振幅都不同的谐和振动（a）、（b）、（c）相加就可组合为一个复杂的振动（d）。

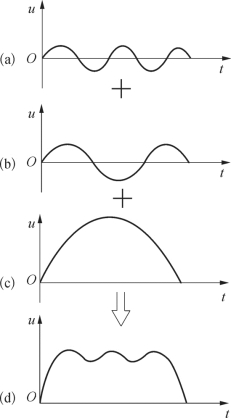
图3—4　谐和波的叠加

无限个谐和振动的振动频率 f 连续地变化，它们各有自己的质点位移振幅A、初相位φ及振动频率 f。每一个这样的谐和振动叫作脉冲地震波的谐波分量。

将脉冲地震波分解为无限个上述谐和振动的过程就是地震波的频谱分解。任一脉冲地震波都可以用数字电子计算机很快实现频谱分解，分解后自动描绘出各谐波分量之间的A与 f 以及φ与 f 的关系曲线，前者称振幅谱，表示为A（f），后者称相位谱，表示为φ（f），二者合称为地震波频谱图。一般主要关心振幅（能量）与 f 的关系，所以常常只用振幅谱来描述地震波的频谱特性，并且通常把它叫作频谱。

从图3—5可知，对于常见的地震波，对应的各个谐波分量能量（振幅）的分布是很不均匀的，频率接近 f0的分量具有最强的能量。 f0称作地震波的主频。显然，地震波的能量较多地分配给主频附近的谐波分量。因此，主频 f0一般与脉冲地震波的视（可见）频率很接近，以致在实际中对它们常不加区分。如果在接收地震波时，地震仪主要把频率接近 f0的一些谐波分量接收下来，也就相当于已经把这个地震波的主要能量接收了。这一点可指导地震勘探野外施工、地震勘探仪器特性的设计与调节、原始资料的再处理，从而在提高地震记录质量方面有重要意义。

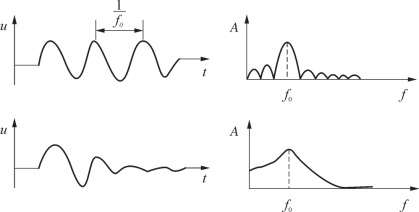
图3—5　脉冲地震波的频谱（振幅谱）

图3—6是野外获得的各种不同类型地震波的能量主要分布频带范围。由图可知：反射、折射波的能量（振幅A）主要分布在40～80 Hz频域内；面波的能量分布在10～30 Hz频域内；交流电干扰的能量分布在50 Hz左右的狭窄频域内；微震干扰的能量分布的频域较宽，其中声波的能量分布在100 Hz以上的较高频域部分。这样，我们就可以利用有效波（反射波、折射波）与干扰波（微震、声波、面波等）频率谱特性的差异，使地震仪各个部分都具有相应的频率滤波特性，主要接收频率在40～80 Hz范围内的反射波、折射波，而把主要能量分布在此频域以外的干扰波滤掉。从而在地震记录上突出了有效波（信号）能量，压制了许多干扰波（噪声）能量，这就提高了地震记录的信噪比，从而有利于清晰识别有效波和提高地震勘探资料解释的质量。

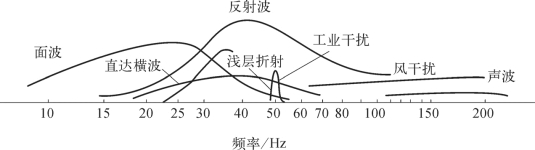
图3—6　地震波的频谱

各种不同震源激发的地震波，或来自不同传播路径的地震波，其波形往往是不同的，也就是说波的频率成分是不同的。地震波频谱特征的分析是地震勘探技术的一个重要方面，如根据有效波和干扰波的频段差异，可用来指导野外工作方法的选择，并给数字滤波和资料解释等工作提供依据。

地震波的频谱分析方法是以傅里叶变换为基础的。上述提到的地震波形函数A（t）是把地震信号表示为振幅随时间变化的函数，是地震波在时间域的表示形式。为了研究地震波的频谱特征，可用傅里叶变换将波形函数A（t）变换到频率域中，得到振幅随频率变化的函数a（f），这种变换过程称为频谱分析方法。

信号在频率域或在时间域的表示是等价的。其对应关系可由傅里叶变换式来表示。它们的数学表达式分别为：

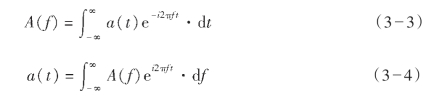
式（3—3）称为傅里叶正变换，式（3—4）称为傅里叶逆变换。

这一对公式非常相似，但积分变量不同，并且表示振动部分的指数符号相反。实际计算时，须将这对积分式离散化，并采用提高计算速度的快速傅里叶变换来完成。

另外，如果研究对象不是地震波振幅随时间变化的振动图形，而是振幅随距离x变化的波剖面图［以函数A（x）表示］，这时亦可用同样的傅里叶变换法对A（x）进行变换，得到的结果称为波数谱，其方法称为波数分析，这在资料处理和解释中也是常用的。

上述的波形图、波剖面图、频谱等反映了地震波能量（振幅）随时间与空间分布的特点。这些特点叫作地震波动力学特点。地震波在传播过程中，它的动力学特点受传播介质（岩层）的性质和结构的影响很大，因此它的变化规律就可能反映了岩层的岩性、结构和厚度。充分研究和利用波的动力学特点，将使地震勘探解决地质问题的能力进一步提高。关于定量应用动力学特征研究岩性的地层地震学，国内已取得了一定的进展。

3）波的吸收和散射

波在介质中传播时，由于波前面的逐渐扩大，能量密度减小，使振幅随距离而衰减，称为几何衰减。但是，由于地质介质的非弹性性质，致使波在传播过程中的衰减比在弹性介质中大，由于介质非弹性所引起的衰减现象称为吸收。因此，波的振幅值A可用下面的经验公式来表示：

式中，A0表示起始振幅，r表示波的传播距离 （以震源为原点），α表示介质的吸收系数。实际观测资料证明，波在致密岩石中吸收现象较弱，在疏松层中吸收作用表现很明显。吸收系数还与波的频率有关，一般介质对高频的吸收作用比低频强。由于各种岩石的吸收性质不一样，因此，可根据吸收系数的测定结果来确定岩石的性质。

当介质中存在着不大于波长的不均匀体时，由于绕射的作用，会形成往各方向传播的波，称为散射。散射的结果使波的高频成分减少，这和吸收作用效果类似。

3.地震波的运动学特点

目前，在生产实践中主要利用地震波波前的空间位置与其传播时间之间的关系，从空间几何形态方面去解决地质构造问题。地震波在传播过程中，波前的时空关系反映了质点振动位相（时间）随空间坐标及波速的分布特点，这种特点叫作地震波运动学特点。研究地震波运动学特点的理论叫作运动地震学。它的基本原理与几何光学很相似，所以又被称为几何地震学。

弹性波运动学在地震勘探中具有重大的实际意义，它是当前地震勘探资料解释中的主要依据。弹性波运动学的基本原理是惠更斯原理和费马原理。利用它可以确定波的传播时间与波前所在空间位置的关系。

下面介绍几个弹性波运动学的基本概念。

1）时间场、等时面和射线概念

地震波在介质空间传播时，其中任意一点M（x，y，z）都可以确定波前到达该点的时间值t，因此波的传播时间可以看作坐标的函数，即

也就是说，根据上述的函数，已知空间任意一点的坐标位置时，就可以确定波前到达该点的时间，所有这样的点就确定了波在介质中传播的标量场，称为时间场。它表明了波前传播时间与其空间位置的关系。时间场函数t（x，y，z，）是定量描述地震波运动学特点的工具。

和重力场、磁力场等概念相似，时间场是指这样一个空间，在这空间任意位置处都有地震波在t时间通过。在时间场中，波前到达时间相等的点所构成的面称为等时面。显然，波前面就是等时面。如果依次给出不同的时间值t1，t2，t3，……，根据给定的波速值，可确定出等时面簇Q1，Q2，Q3，……的空间位置（如图3—7所示）。

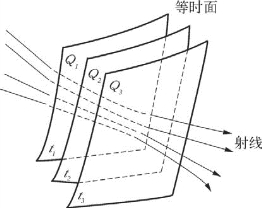
图3—7　等时面簇和射线簇

地震波的传播，除了可用波前来描述外，也可用射线来直观地表示。所谓射线，就是波从一点到另一点传播的路径，它代表了波传播的方向。因此，射线应与各等时面的法线方向一致，即射线与各等时面正交。等时面方程为：

在已知时间场内，可以有许多条射线，它们的集合就是射线簇。若已知空间射线簇位置和波沿其中任一条射线传播的时间，就可以确定这个波的时间场。所以，时间场可以用等时面簇或射线簇两种概念来描述，二者呈正交关系（如图3—7所示）。等时面和射线是时间场的两种表示方法，由于介质性质不同，波传播的时间场分布规律就不一样，因此研究等时面和射线的分布规律就可以了解波在介质中的传播情况。

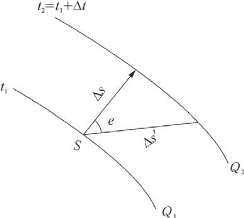
图3—8　时间场的梯度方向

根据场论可知，任何一种场的分布，都可以用等值面和力线来表示，时间场也不例外，等时面就是等值面，而波射线则相当于力线，波射线的方向就是时间的梯度方向。如图3—8所示，假设地震波在某时刻t1位于Q1位置，经过Δt时间后于t2时刻（t2＝t1+Δt）到达Q2位置，之间垂直距离为Δs，波传播速度为，按梯度定义可表示为：

在三维直角坐标中，上式梯度可写成矢量表达式为：

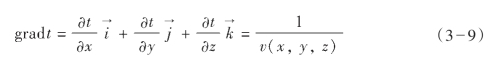
实际上，速度（x，y，z）函数是空间各点的绝对值，方向是未知的，因此将矢量表达式（3—9）平方后可写成其标量式：

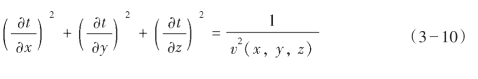
式（3—10）称为射线方程，是几何地震学中的基本方程式，它表示地震波在传播过程中所经过的空间与时间的关系。要求得此方程的解，首先必须知道地震波的传播速度、t＝t0时刻的初始条件和一定的边界条件。例如，在均匀各向同性介质中，波的传播速度是常数，该方程的解为：

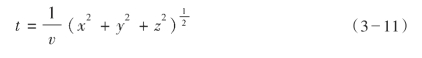
这是一个球面方程，说明在均匀各向同性介质中地震波的波前是一系列以震源点为中心的球面。

2）费马原理（射线原理）

波的传播除了用波前来描述外，还可以用射线来描述。所谓射线，就是波从这一点到另一点的传播路径，波沿射线传播的时间和其他任何路径传播的时间比起来是最小的，这就是费马的时间最小原理。用射线来描述波的传播，往往使问题的讨论更为简便了。

在均匀介质中，因为波的传播速度各处都一样，其旅行时间正比于射线路径的长短，波从这一点传播到另一点，其最短的射线路径是直线，所用的时间比其他任何路径都要小。在地震勘探中，在均匀介质的假设条件下，射线为自震源发出的一簇辐射直线，射线恒与波前垂直。对于平面波，它的射线是垂直于波前的直线。

用射线和波前来研究波的传播，是一种用几何作图来反映物理过程的简单方法，它只说明波传播中不同时刻的路径和空间几何位置，不能分析能量的分布问题，所以称之为几何地震学，在地震勘探的基本原理、方法及资料解释中常用这种方法来分析地震波场的特征。

3）惠更斯原理（波前原理）

为了进一步了解波前的运动过程，举例说明下列常见的现象。如图3—9所示，AB是一道长堤，中间有一桥涵洞a，当一系列水面波自堤外向堤内传播时，被堤阻挡不能通过，但堤内仍然可以激起水面波，可以看到这些水面波好像是以桥涵洞a为波源发出的半圆形波，称为元波前，它与原来波前的形状无关，这一现象称为波的绕射。所谓“波前原理”（也叫惠更斯原理），即介质中传播的波，其波前面上的每一个点，都可以看作是波向各个方向传播的波源（点震源）。

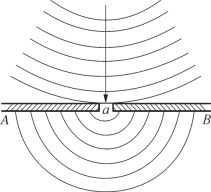
图3—9　波通过桥涵洞时的运动过程

对于理解波的传播过程，惠更斯原理非常重要，并常用于绘制连续的波前。惠更斯原理的定义是，在波前面上的任意一个点，都可以看成是一个新的震源，其中隐含的物理意义是，在同一波前面上的每一个质点，都从它们的平衡状态开始，基本上以同一方式振动。因此，在其相邻质点上，弹性力会由该波前的振动产生变化，因而会迫使下一个波前的质点运动。这样，惠更斯原理就能解释扰动怎样在介质中传播。更具体一点说，对于给定的某时刻波前的位置，把该波前的每一个质点都作为新的震源，可以确定将来某一时刻波前的位置。在图3—10中，AB是在t0时刻的波前。在时间间隔Δt内，波传播的距离为Δt，其中　是地震波的传播速度（它可以随空间变化），在t0时刻的波前上选一系列点P1，P2，P3，……，以这些点为圆心，以Δt为半径画弧，只要选择了足够的点数，这些弧的包络就形成了新的波前，随着点数的增加，所绘制的波前也会达到任意精度，在该包络之外，波会产生相消干涉，使它们的效应相互抵消，当AB是一个平面，速度是一个常数时，只需要选两个点数，画两个圆弧，作一条和两个圆弧相切的直线，就会得到新的波前位置。需要注意的是，惠更斯原理只给出相位信息，不能给出振幅的大小。

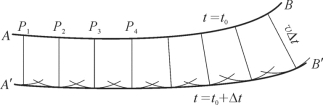
图3—10　利用惠更斯原理确定新的波前面

4）惠更斯—菲涅耳原理

在前面的讨论中，我们只研究了波前或射线的时空关系，未涉及波动的本性——波的干涉和衍射。从图3—10中可以看出：t0时刻的波前AB上各点都是新震源，它们产生的子波向前传播，经过Δt时间间隔后形成t0+Δt时刻的新波前A′B′。同时，AB波前上各震源产生的子波也在向后传播，经过Δt时间后，似乎在t波前的后方也存在一个t0+Δt时刻的新波前A″B″。换言之，波在向前传播的同时，还存在一个向后传播的倒退波。然而，在实际上这个倒退波是观测不到的。可见，前面介绍的理论并不完全符合客观实际，它还存在一些缺陷，需要进一步加以解决。

19世纪初，菲涅耳以波的干涉原理弥补了惠更斯原理的缺陷，将其发展为惠更斯—菲涅耳原理。它的基本思想是：波在传播时，任意点P处质点的振动，相当于上一时刻波前面S上全部新震源产生的所有子波相互干涉（叠加）形成的合成波。这个合成波可以用积分进行计算。由对P点合成波进行的数学计算可以证明：波在传播时，t时刻波前上各新震源产生的子波在前面任意新波前处，发生相长干涉，而出观较强的合成波；在后面的任意点处，发生相消干涉，合成波振幅为零，使倒退波实际不存在，因而使理论终于与实际完全一致了。

根据惠更斯—菲涅耳原理，不但可以研究波的运动学特点（波前或射线的时空关系），而且可以研究波的动力学特点（波的能量随时空的分布规律）。这样全面地研究地震波的全部物理学特点的理论被叫作物理地震学。

生产实践和理论证明，在复杂的多断层地区，应用物理地震学可以提高地震勘探工作的精度。

在地震波波长λ与弹性分界面的尺度a（长度或宽度）及界面埋藏深度h相比不能近似为无限小的情况下（即在的条件不成立时），几何地震学的一些定律（如波沿射线传播或波的能量沿射线传播等）就不是完全精确的。这时必须借助于惠更斯—菲涅耳原理，利用积分公式（3—12）去进行研究。

继菲涅耳之后，德国学者基尔霍夫导出了计算P点合振动振幅公式。设S为包含有震源O的任意形状在t时刻封闭的波前面，则在S面以外任意点P处，由S面子波震源激起的合成波振幅AP，可用下式求出：

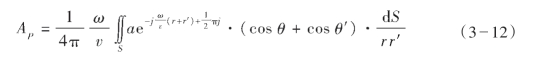
式中，a为震源O处初振幅，为介质中波速，ω为波动圆频率，r、r′、θ及θ′为如图3—11所示的距离及角度；n→ 为面积单元dS的法向量。

(www.xing528.com)

图3—11　惠更斯—菲涅耳原理示意图

一般情况下，式（3—12）是一个相当复杂的积分，使用起来不是十分方便的。幸而在大部分情况下，地震勘探的施工地区能近似满足的条件，用几何地震学作为物理地震学的一种近似，精度相当高，可以满足生产上的需要，而且这种近似大大简化了地震勘探的理论与方法。为此，在下面的叙述中，均只讨论与几何地震学（即运动地震学）有关的内容。

由惠更斯原理和费马原理可以推导出波动的斯奈尔定律（反射—折射定律），其内容早已为读者熟悉。因为它们是几何地震学中最常用的基本定律，所以这里只做简要的介绍。

5）斯奈尔定律

在几何光学中，当光线射到空气和水的分界面时，会发生反射和折射，并服从斯奈尔定律。地震波在地下岩层中传播，遇到弹性分界面时也会发生反射、透射和折射，从而形成反射波、透射波和折射波。地震勘探中所说的透射波是指透过界面的波（相当于几何光学中的折射波），所说的折射波是一种在特殊条件下形成的波。

（1）反射波

如果地震波以α角入射到介质分界面，它的一部分能量经界面反射，以α角出射形成反射波，另一部分能量则透过界面，以β角折射至下一个岩层，形成透射波，则称α角为入射角，α′为反射角，β为透射角（如图3—12所示）。

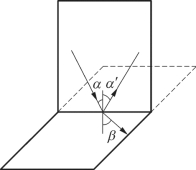
图3—12　射线平面

① 反射定律

在几何光学中，用射线、平面波和惠更斯原理，证明入射波入射到界面时射线的变化规律，即反射定律。它告诉我们入射角等于反射角；入射线、反射线位于反射界面法线的两侧，入射线、反射线和法线同在一个平面内，此平面叫作射线平面，它和弹性分界面垂直（如图3—13所示）。在地震勘探中，当我们沿某一测线激发和接收地震波时，入射波和反射波都位于过测线并和反射界面相垂直的射线平面内。反射定律只说明了入射波和反射波之间的关系，并没有讨论在什么条件下弹性分界面才能产生反射。

图3—13　垂直入射时的反射与透射

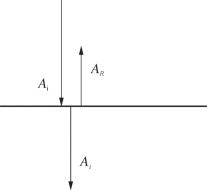
② 反射波的形成

反射系数：设入射波的振幅为Ai，反射波的振幅为AR，反射波和入射波振幅之比叫作反射界面的反射系数，用字母R表示，写为：

根据反射理论，可证明当波垂直入射到反射界面上时，如图3—13所示，反射系数为

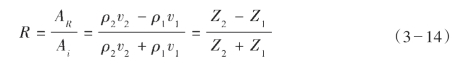
式中，ρ1、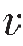1、ρ2、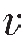2表示分界面上下两种介质的密度和波在两种介质中传播的速度，ρ11＝Z1，ρ22＝Z2表示上下介质的波阻抗。

反射系数写成一般式为：

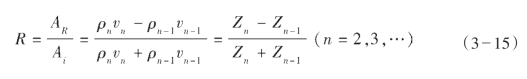
反射系数的物理意义是说地震波垂直入射到反射界面上后，被反射回去的能量的多少，这说明了在界面上能量的分配问题。

形成反射波的条件：当R＝0，即Zn＝Zn—1时，不产生反射，这实际上是一种均匀介质，不存在弹性分界面，只有Zn≠Zn—1，即R≠0时，才产生反射，所以形成反射波的条件是地下岩层中存在着波阻抗分界面。在实际的沉积岩层中，密度随深度变化的数量级远比速度变化要小，可假设它为常量，这时反射系数可简化为：

假设随深度增加，有波传播的速度分别为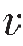1＝2 500 m/s、2＝3 500 m/s、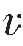3＝4 500 m/s的岩层，则按上式计算出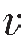1与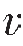2层之间界面的反射系数为0.17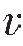，2与3层之间界面的反射系数为0.12。虽然速度随深度增加而增大，按上式计算反射系数时，公式中分母随深度增加而增大，而分子却不相应地增长（都为1 000 m/s），就出现随深度增加反射系数变小的现象，这是反射波振幅随深度增加而变弱的原因之一。

反射波强度：从式（3—14）可知反射系数与上下岩层的波阻抗差成正比，差值越大，R值越大，反射波越强；反之越弱。如果在陆相碎屑岩沉积中出现含油气构造，构造部位的储集层为含油气砂岩（如图3—14所示），砂岩一旦含油气，速度会明显降低，从而与围岩（泥岩）形成一个较强的波阻抗界面，出现较大的反射系数，在地震记录中会出现特强的反射波，说明反射系数的大小与地层的岩性及含油气直接有关，它是影响反射波振幅强弱的一个主要地质因素。

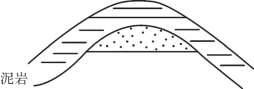
图3—14　含油气的砂岩构造

反射波的极性：R有正负值的问题，当Zn＞Zn—1时，则R＞0，反射波与入射波的相位相同，都为正极性，在地震记录上认为初至波是上跳的（同相）；反之，R＜0，为负值，反射波为负极性，入射与反射波反相，相位相差180°。

R的取值范围：R值的定义域为—1≤R≤1。在实际地层中，因沉积间断所形成的侵蚀面（不整合面）上，老地层直接与新地层接触，它们之间在密度和速度上往往存在着较大的差异，从而形成一个明显的波阻抗界面，产生较强的反射波。

（2）透射波

① 透射定律

当入射波透过反射界面形成透射波时，由于分界面两侧波传播的速度不同，透射波的射线要改变入射波射线的方向，而发生射线偏折现象，偏折程度的大小决定于透射定律。它告诉我们入射线、透射线位于法线的两侧，入射线、透射线、法线在同一个射线平面内；入射角的正弦和透射角的正弦之比等于入射波和透射波速度之比，或者说入射角、反射角和透射角的正弦与它们各自相应的波速的比值等于一个常数值，这常数值称为射线参数，写成数学式为：

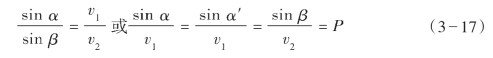
上式为斯奈尔定律的数学表示式。它说明入射角与反射角、入射角与透射角之间的关系，也是反射和折射定律的一个统一表达式，故斯奈尔定律也称为反射—折射定律。

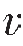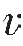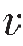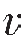从上式可知，当1＞2时，则α＞β，透射波射线靠近法线偏折，这种现象就是几何光学中所讲的光从空气射到水中，射线发生折射的现象；当1＜2时；则α＜β，透射波射线远离法线，而向界面靠拢，在实际的地层中，波的透射多属于这种情况。

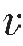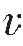如果有三层或多于三层的介质，并假设波传播的速度是递增的，即3＞2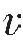＞1，根据斯奈尔定律，波从第一层传播到第三层时，射线是一条折射线，即在层状介质中波传播的射线为折射线。

② 透射波的形成

透射系数：设透射波的振幅为A，可得透射系数T为：

透射系数的物理意义是入射波的能量转换成透射波的能量的多少。

当波垂直入射时，据反射和透射系数公式，可得：

则透射系数又可写为：

形成透射波的条件：从上式可知，当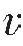n—1≠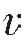n时，才能形成透射波，即形成透射波的条件是地下存在速度不同的分界面，简称为速度界面，而把波阻抗分界面简称为反射界面。对一般的沉积地层，反射系数一般为0.2，甚至更小，这时T≠0，总可以形成透射波。

透射波的强度：当入射波振幅Ai一定时，T越大（R越小），透射波越强（反射波越弱）；反之，T越小（R越大），透射波就越弱（反射波就越强）。

透射波极性：无论Zn＞Zn—1 或Zn＜Zn—1，T总为正值，透射波和入射波同相。

在上述讨论反射波、透射波时，只简单假设两个界面，但在实际的沉积地层中，往往有多个分界面，地震波从激发入射到第一个界面，一部分能量被反射，另一部分能量透过界面成为透射波，该透射波到第二个界面，又发生反射与透射，这样进行下去，到了深部，反射波返回到地表，能量已变得很小，这样就出现了浅部界面的反射波能量较强，而深部由于反射界面的增多，使地震波的能量变得很小。

（3）折射波

① 折射波的形成

假设有一个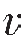2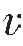＞1的水平速度界面，如图3—15所示，从震源发出的入射波以不同的入射角投射到界面上，据斯内尔定律可知，随着入射角α的增大，透射角也随着增大，使透射波射线偏离法线向界面靠拢，当α增大到某一角度时，可使β＝90°，这时透射波以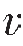2的速度沿界面滑行，形成滑行波，称使β＝90°时的入射角为临界角i，记为：

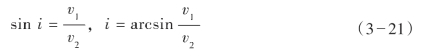
如果已知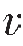1、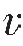2，就可由上式求出临界角。

根据波前原理，高速滑行波所经过的界面上的任何一点，都可看作从该时刻振动的新点源，这样下伏介质中的质点就要发生振动，由于界面两侧的介质质点间存在着弹性联系，必然要引起上覆介质质点的振动，这样在上层介质中就形成了一种新的波动，在地震勘探中称它为折射波。它好比顺水航行的船，当船速大于水流速度时，在船头就会看到一种向岸边传播的水波，它就是折射波。

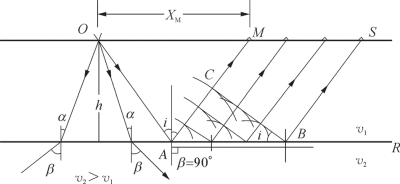
图3—15　折射波的形成

② 折射波的波前、射线和盲区

折射波的波前是界面上各点源向上覆介质中发出的半圆形子波的包线，从图3—15可见，滑行波自A点以速度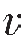2滑行了一段时间Δt，波前到达B点，则AB＝2Δt，同时A点向上覆介质发出半圆形子波，其半径为AC＝1Δt，从B点作A点发出子波波前圆弧的切线BC，就为该时刻的折射波的波前，可证明它与界面的夹角∠ABC为临界角i，由△ABC为直角三角形，可得：

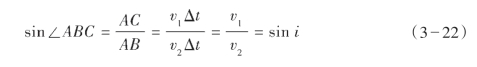
折射波的射线是垂直于波前BC的一簇平行直线，并与界面法线的夹角为临界角。射线AM是折射波的第一条射线，在地面上从M点开始才能观测到折射波，所以称M点为折射波的始点，自震源到M点的范围内，在地面观测不到折射波（或说不存在折射波），称这个范围为折射波的盲区，表示为XM，其数值为：

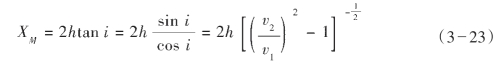
从式（3—23）可知，XM随着h的减小和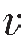2/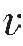1比值的增大而减小。在一般情况下，假设取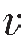2/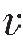1为1.4时，则XM＝2h，因此作为一条经验法则，折射波只有在炮检距大于两倍折射界面深度时才能观测到。

③ 折射波的形成条件

在上面的讨论中，简单地假设了只有一个界面的地层模型，这时要形成折射波，必须是下伏介质的波速大于上覆介质的波速。在实际的多层介质中，一般速度随深度增加而递增，因而可形成多个折射界面。但是上下地层速度倒转的现象在油气田、煤田等地层中也是经常发生的，即在地层剖面中，中间可以出现速度相对较小的地层，在这地层的顶面就不能形成折射波。用斯内尔定律可以证明，在多层介质中，要在某一地层顶面形成折射波，必须是该层波速大于上覆各层介质的速度。与形成反射波的条件相比，在同一沉积的一套地层中，折射界面的数目总小于反射界面，因此说形成折射波的条件比反射波要苛刻。

6）转换波

当纵波斜入射到反射界面时，由于介质质点振动可分为垂直和平行界面的两个分量，弹性介质受到两种应力与应变，在上下介质中可分别形成反射纵波RP、反射横波RS、透射纵波TP、透射横波TS。称与入射纵波波型相同的RP、TP为同类波，与入射纵波波型不同的RS、TS为转换波，根据斯内尔定律，各种波的传播方向与波速之间的关系为：

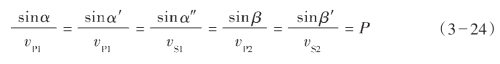
式中，α是入射角，α′、α″分别为纵波和横波的反射角，β、β′分别为纵波和横波的透射角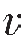，P1、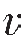S1分别为反射纵波和横波的速度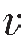，P2、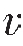S2分别为透射纵波和横波的速度。

在同一介质中，由于纵波的传播速度大于横波的传播速度，从式（3—24）可知有α′＞α″、β＞β′的关系，据此可作出纵波斜入射到界面时波分裂和转换的示意图，如图3—16所示。从图中可看出，入射波在界面上被分裂为四个波的能量，从波动的理论可导出这些波的能量分配方程，不同波能量的大小主要与界面两侧介质的密度比、速度比和入射角大小有关，简称AVO。当炮检距较小（入射角较小）时，由于质点振动水平分量很弱，使反射波振幅变化也很小。在实际的地震勘探中，炮检距相对深达数千米的反射界面来说，一般都是比较小的，这样从震源投射到界面再反射回地面的反射波是近似法线反射的，所接收的主要是纵波反射信息。近法线反射（或叫近法线入射）与小入射角、小炮检距的提法在物理意义上是等同的。当地震波垂直入射时，不产生转换波，可以从能量方程中导出上面所提到的反射和透射系数公式。

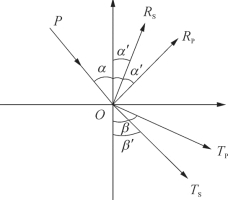
图3—16　纵波斜入射时波的分裂和转换

7）时距曲线

前面我们曾讨论了反射波和折射波的形成以及它们的波前、射线在空间的分布特点。实际上，对这些特点的观测工作，一般都不能到地下去进行，而只能在地面（沿测线）进行。我们沿测线各观测点可测得某种地震波的波前（或射线）到达时间t与这些点的坐标x之间的时空关系t（x），t（x）在t—x直角坐标系中的图形称为时距曲线，如图3—17所示。它实际上反映了该种地震波时间场在测线上的分布规律。通过时距曲线资料的观测，可以分析波在地下介质中的传播规律，从而确定地震界面的深度及形态等特征，并解决地质问题。

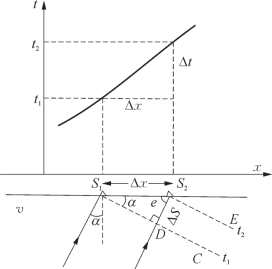
图3—17　时距曲线（图中测线以下为射线平面）

（1）反射波时距曲线

最简单的二维问题就是图3—18所画的水平地层，反射层AB离震源S距离为h，S点震源激发，沿方向SC传播，在界面上产生反射波，反射角与入射角相同。在C点反射角与入射角相等，根据这个特点可以确定反射路径CR。更容易的方法是利用虚震源（镜像点）I，I位于炮点S与反射面的垂线上，在反射层的另一面，与S点到反射界面的距离相等。将I与C点连接，并将直线延长到点R，CR就是反射路径（由于CD平行于SI，所有的角度都等于α）。

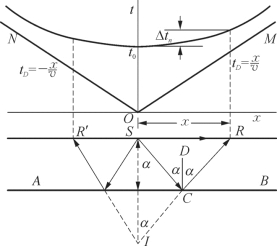
图3—18　水平反射层的旅行时间曲线

设　是平均速度，反射波的到达时间t是（SC+CR）/。由于SC＝CI，所以IR与波传播路径SCR的长度相等，因此，t＝IR/，如果变量x是炮检距，则

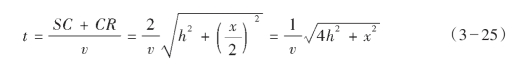
或

所以，时距曲线是双曲线，如图3—18的上半部分所示。曲线顶点坐标为（2h/，0），渐近线的斜率为：

这个斜率实际上就是直达波时距曲线的斜率，传播路径是SR。由于SR总是小于SC+CR，所以直达波总是先到。直达波的旅行时间是，时距曲线是过原点的直线OM和ON，斜率为±1/。当x变得很大时，SR与SC+CR之间的差别变小，反射波旅行时间与直达波旅行时间逐渐接近。利用在炮点的检波器记录到的旅行时间t0可以确定反射层的深度。设式（3—25）中的x＝0，可以得到

如果画出t2和x2的曲线取代图3—17的t—x曲线，可以得到直线的斜率1/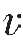2和截距，这就是确定速度的著名的“x2—T2方法”的基础。

（2）正常时差

时距曲线在t轴上的截距，在地震勘探中叫t0时间，即：

它表示波沿界面法线传播的双程旅行时，有时也叫回声时间，此时式（3—25）可以写成以下几种形式：

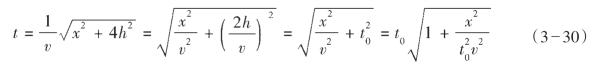
可以从式（3—30）中由地震记录求出旅行时间t。通常2h＞x，则可以用下面形式的二项式展开：

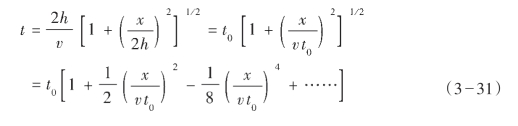
如果t1，t2，x1，x2是两个不同的旅行时间和炮检距，则可以得到第一个估计值

在特殊情况下，当一个检波器在炮点时，Δt是正常时差（NMO），用ΔtNMO来表示

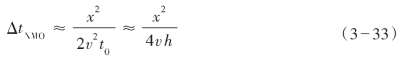
有时，也保留展开式的另一项：

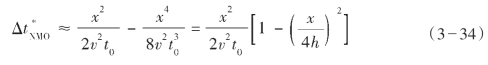
从式（3—40）中可以看出，正常时差随炮检距x的平方增加而线性增加，与速度的平方成反比，与炮点的旅行时间成反比（也就是与反射层的深度成反比），如式（3—28）所示。因此随着炮检距的增加，反射曲线的曲率快速增加，同时随着记录时间的增加，曲率的变化变小。