砂性土临界状态模型参数研究成果

土力学临界状态的发展和临界状态模型的提出是岩土工程学科的重大进步（Schofield and Wroth，1968）。土体中的临界状态是指土体在体积和有效应力不变化的情况下，剪切应变仍持续发展达到流动的最终状态。临界状态模型的优点是破坏标准考虑了体积的变化，而摩尔库仑模型的破坏标准只是基于最大应力定义的。

在临界状态模型中，用应力不变量q和p［见式（4.1）和式（4.2）］代替τ和σ。相应地，用（q，p）坐标系中斜率为M=qcs/pcs的破坏线代替摩尔库仑（τ，σ）坐标系中斜率为tan φ=τcs/σcs的破坏线。同时，用（e，ln p）曲线代替（e，lnσ）曲线，且将e-ln p曲线的斜率定义为λ。临界状态模型的核心思想是在（q，p，e）坐标空间内，土体的破坏存在一个唯一破坏曲面。

Mooney等（1998）对砂土的临界状态进行了一系列的研究。研究发现，在平面应变试验中，只有剪切带内土体达到或符合临界状态的概念。剪切带内土体的切应力不变，体积也不变。Mooney等绘制的q-p'曲线和e-p'曲线见图7.3。

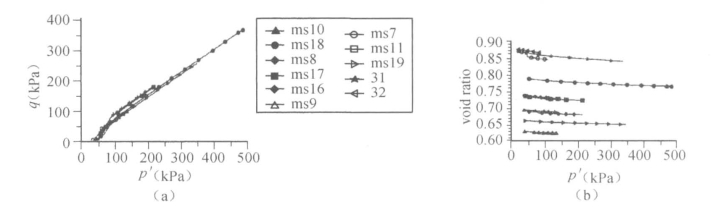
图7.3　Mooney等（1998）绘制的q-p'曲线和e-p'曲线(www.xing528.com)

本书中平面应变和三轴压缩试样临界状态下的q-p曲线和e-ln p曲线见图7.4。从图7.4（a）中可以看出，平面应变试样和三轴压缩试样的（qcs，pcs）点分别沿不同的直线，而与初始孔隙比和围压大小无关。这与图7.3所示的Mooney等的结论一致。平面应变试样的qcs-pcs斜率（Mps=0.86）比三轴压缩试样（Mctc=1.06）小，这表明相同荷载条件下应力比相同，不同荷载条件应力比不同。Mooney等认为对一种砂土，平面应变试样的M是定值，是一个材料特性参数。从本书结果看，这一材料特性参数与荷载条件有关，即不同荷载条件下这一参数值不同。

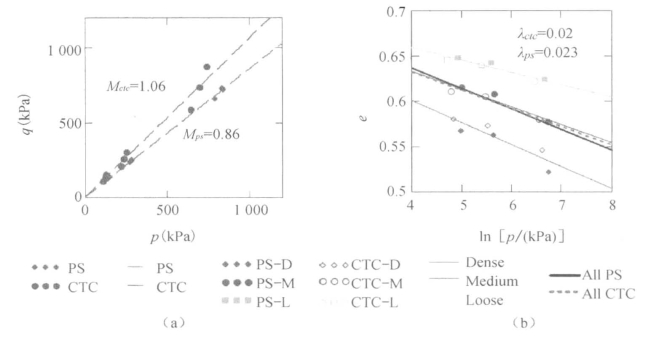
图7.4　平面应变试样和三轴压缩试样的q-p曲线和e-ln p曲线

图7.4（b）为不同条件下试样的e-ln p曲线，从图中可以发现，初始孔隙比相同的试样的（ecs，ln pcs）点近似在同一条直线上，而与荷载条件无关。这同样与Mooney等的结论相一致，Mooney等认为初始孔隙比相同的砂土可能具有同一条临界状态直线。虽然Mooney等没能对这一结论进行验证，但是这一结论与后来一些学者提出的砂土的最终密实度概念的研究结果相一致（Evans，2005；Narsilio and Santamarina，2008）。本书的数值模拟结果也对这一结论进行了验证，即所有试样的临界状态直线的斜率一致，与荷载条件无关，但临界状态直线的截距不同，取决于试样的初始孔隙比。计算平面应变试验和三轴压缩试验的λ值，发现它们非常接近（λps=0.023和λctc=0.020）。因此，本书可以得到与Mooney等相同的结论，即e-ln p曲线的斜率和λ都是材料的特性参数。

综上所述，应力比、M、e-ln p曲线的斜率、λ都是材料参数。但是M是与荷载条件相关而与初始孔隙比以及围压无关的参数，而λ是与初始孔隙比有关而与荷载条件无关的参数。这一结论与Mooney等（1998）研究结论相一致，即一种砂土的临界状态孔隙比不是唯一的，而与试样的初始孔隙比以及荷载条件有关。