砂性土颗粒方向分布统计分析

颗粒方向由颗粒长轴与水平坐标轴间的逆时针夹角表示。计算出每个颗粒方向后，颗粒方向的分布可以用极坐标直方图表示，极坐标的半径表示某一指定角度范围内的颗粒方向分布个数的多少。由于计算颗粒方向时夹角范围为0°到180°，但是颗粒方向是双向的（角度可以是θ也可以是θ+180°）。所以通过将0°～180°间的分布图经原点对称映射于180°～360°之间来绘制一个完整的极状分布图。

在分析二维颗粒方向分布时，采用圆形统计法。在圆形统计法中，θi为数据中的第i个观测角。颗粒的平均方向，即所有颗粒方向的合成矢量方向可以表示为

合成矢量平均长度：

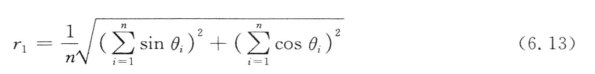
r1位于0～1之间，且具有一定意义。r1=1表示所有颗粒具有相同方向，即完全各向异性。r1越小表示颗粒方向分布范围越大，越倾向于各向同性。但是，r1=0不一定是所有颗粒方向均匀分布。

式（6.12）和式（6.13）是基于颗粒方向的分布范围为0°到360°，但是测得或计算得到的颗粒方向由于双向分布所以为0°到180°。因此，Krumbein（1939）提出了一种修正计算法：

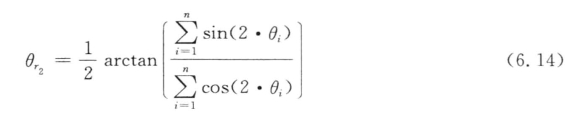
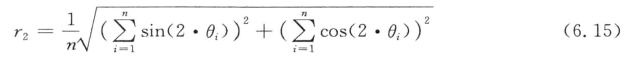
上面的公式都是针对通用的圆形数据。在对颗粒方向的分析过程中，采用上述公式计算颗粒方向时的一个假设是所有颗粒的权重相等，而不考虑颗粒大小的影响。Yang（2002）认为当材料中小颗粒较多时，忽视颗粒大小的影响可能会导致分析结果的错误。他指出，如果试样中小颗粒过多，极状图主要受小颗粒方向的影响，而主要的力链或力柱是由颗粒材料中大颗粒形成的（Iwashita and Oda，2000），从而试样的行为特性受大颗粒影响显著。为了避免这种情况，Yang提出了一种考虑颗粒大小权重的算法来计算颗粒方向的分布，即在计算平均方向以及平均方向长度时，考虑采用每个颗粒面积占所有颗粒总面积的比重，式（6.14）和式（6.15）变为(www.xing528.com)

根据这一定义，颗粒方向分布的整体特性可以通过除极坐标直方图以外的平均方向和平均方向长度来表示。

由于本书采用的颗粒是由两个球重叠而成高宽比为1.5∶1的块颗粒，因此与真实土颗粒或二维数值模拟中的颗粒不完全相同，所以模拟的结果与试验结果有所出入，与二维模拟的结果也不完全一致。因为是采用两个球重叠而成的块颗粒，所以三维试样的切面上会出现很多实心圆（尽管这只是一个虚拟的切面）。而真实土颗粒是不规则的，所以这一现象不会出现在实验室中，也不会出现在二维模型中。切面上实心圆的出现可能会对本书中的颗粒方向分布的分析造成较大的影响，因为颗粒的方向定义为颗粒长轴的方向，但是圆形颗粒的方向是任意的（无法决定颗粒方向），所以在分析颗粒方向分布时，首先要剔除切面上的实心圆，否则会对计算结果造成误差。剔除切面实心圆后，另一个需要注意的是试样边界的影响。研究发现，与边界墙相接处的颗粒的方向更容易与边界方向一致，所以边界会对其周围颗粒方向造成影响，影响颗粒方向分布的分析。考虑到上述因素的影响，所以在生成颗粒方向极状图之前要采取两个步骤：一是剔除切面上的实心圆；二是剔除与边界墙相接触的颗粒。这两个步骤将会提高颗粒方向分布图的合理性和准确性。图6.33（a）、（b）、（c）分别为不考虑实心圆和边界影响、只考虑实心圆影响、考虑实心圆和边界影响三种情况时颗粒方向极状图的示例。

颗粒方向分布极状图生成之后，需要分析整个材料中颗粒方向的分布是否有明显的统计意义上的方向性，或者颗粒的方向计算是否由于各向同性而为随机任意值［当颗粒方向各向同性分布，式（6.17）平均方向长度为0，所有颗粒方向一致］。Fisher（1993）提出的Rayleigh测试可以评估单峰值数据的均匀性。Rayleigh法假设所有数据均匀分布，当合向量长度r大于测试值，假设不成立，即试样不是均匀分布。测试值计算公式如下：

式中，n为样本（颗粒）数目，Z是n·r2在某一指定或重要P值时的临界值。这里P值取为5%，且当临界值（Z）大于3时，认为平均方向的计算是合理的（即不是均匀分布的情况下的任意值）。

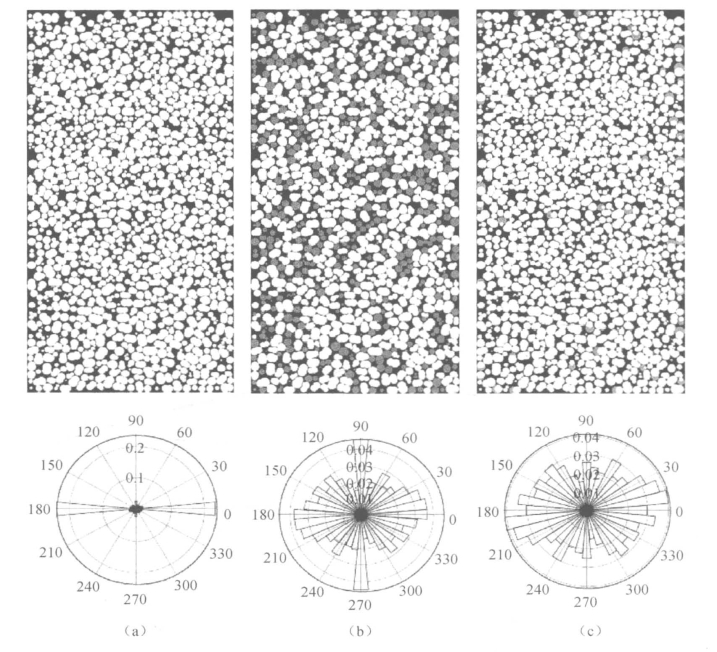
图6.33　颗粒方向极状分布图（CTC-D75-00）

（a）不考虑实心圆和边界影响；（b）只考虑实心圆影响；（c）考虑实心圆和边界影响