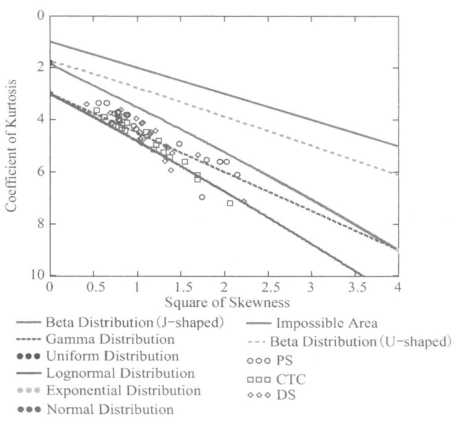
图6.3 Pearson概率分布图
统计模型用来表征局部孔隙比的分布情况。对数值模拟数据的局部孔隙比分布建立统计模型,主要有三个步骤:选择分布函数,选择拟合方法,测试所选分布函数和拟合方法的拟合度。Pearson和Hartly(1954)提出了Pearson概率图,Harr(1988)建议用该图选择分布函数,许多学者采用了这一方法(Evans,2005)。本书也采用这种方法来选择分布函数。Pearson概率图中,纵坐标为峰度系数,横坐标为偏度平方,选用不同分布函数将坐标区划分为多个区域,根据所给数据在Pearson概率图中的分布位置便可以选择合适的分布函数。图6.3所示为Pearson概率分布图,以及数值模拟的孔隙比分布统计参数的分布情况。从图中可以看出,伽马分布和对数正态分布与局部孔隙比的拟合度较高。
分布函数确定之后,对数据分布拟合的方法通常有三种:最大似然估计法、概率分布函数直方图拟合、累积分布函数拟合。最大似然估计法受离散数据的影响较小,且函数参数慢慢逼近直方图中真值。考虑到试样尺寸和数据量较大,本书采用最大似然估计法。(https://www.xing528.com)
最后,采用Finkelstein和Schafer(1971)提出的Kolmogorov-Smirnov-type检验法来检验选定的分布函数及拟合方法的拟合度。Kolmogorov-Smirnov检验主要评估L∞值,该值是真实值与计算值的最大绝对差。
基于以上讨论,本书选择伽马分布函数,采用最大似然估计对数据进行拟合。通过Kolmogorov-Smirnov法检验数据拟合度。直方图的概率分布拟合图示例见图6.4。
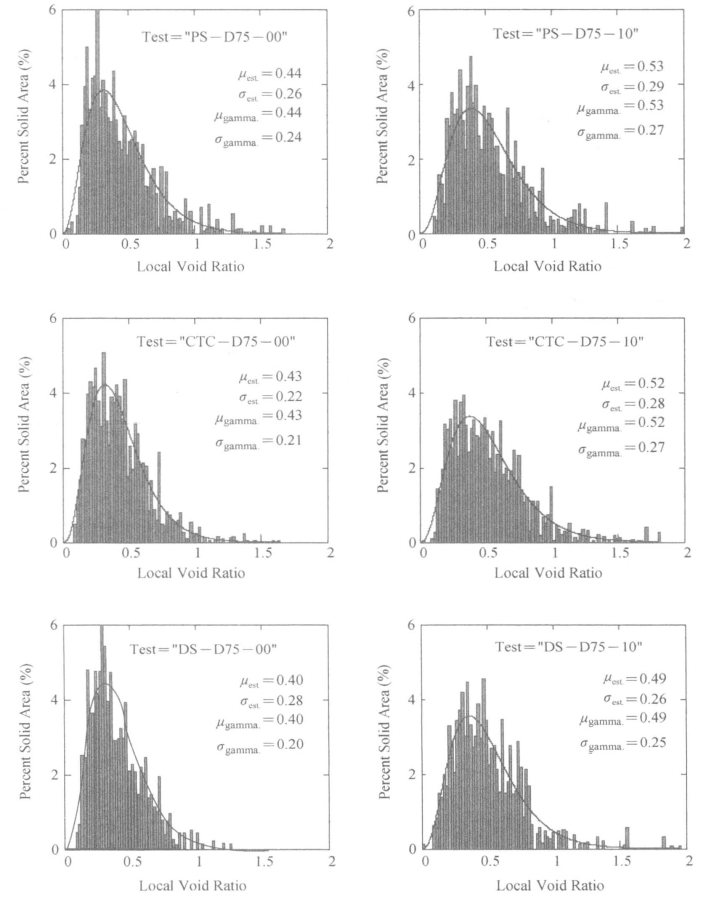
图6.4 直方图概率分布拟合图示例
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




