接触参数分析在砂性土宏细观特征数值分析研究中的应用

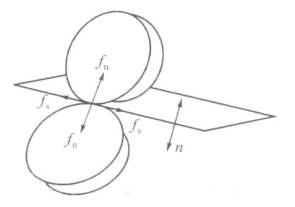
图5.47　颗粒接触点处细观力学分析图解

（Bathurst和Rothenburg，1990）

5.4.3.1　简介

从细观层面看，每个颗粒配位数、接触方向分布、接触法向力和切向力的大小和分布等，都是颗粒材料细观结构和细观力学的重要参数。配位数，也就是每个颗粒的平均接触颗粒数目，在之前的章节已经讨论过。为了进一步分析颗粒的细观结构和细观力学，下面讨论接触点法向量、接触法向力、接触切向力的分布。

图5.47所示为颗粒材料接触点处细观力学分析图解，图中n为接触面的法方向，接触面的法方向即为接触方向，fn为法向力，fs为切向力。

当颗粒材料剪切变形时，主要承受剪切力，配位数、颗粒间接触方向、接触力都会发生变化。在不同的荷载作用下，接触方向和接触力的发展变化是不同的。通过对不同荷载作用下颗粒材料接触方向和接触力的分析，可以深入理解材料细观结构和细观力学特性。

5.4.3.2　接触点法方向分布

利用离散单元法数值模拟，可以很方便地获得颗粒间接触方向的信息。数值模拟分析中，可以获取任意应变状态下每一个接触点的接触单位法向量（xc，yc，zc）。知道接触单位法向量后，接触方向在球形坐标系中可以表示为

当每个接触方向已知时，采用与分析颗粒方向相同的方法，可以通过球形柱状图表示颗粒间接触方向的分布。采用Leopardi（2006）提出的递归等面积球形分区法对单元球体进行分区。用接触方向位于每一立体角范围内的接触数占总接触数的百分数表示球形柱状图中该立体角方向的半径，便可得到接触方向分布的球形柱状分布图。

图5.48到图5.53所示为低围压下不同密实度试样在不同荷载条件下的接触方向分布的球形柱状分布图。与分析颗粒方向时相同，每幅图中包括三个垂直于不同坐标轴的平面图和一个三维立体图。y-z平面图和x-z平面图表示竖直投影面上接触方向的分布，x-y平面表示水平投影面上接触方向的分布。

用椭球对图5.48至图5.53所示的接触方向的分布进行拟合，从而可以用标量分析的方法来表示接触的主要方向分布。对接触方向分布各向异性程度的一阶量化分析时，首先要求出椭球的半轴比。图5.54（a）、（b）、（c）所示分别为平面应变、三轴压缩和直剪条件下椭球的半轴长度比。a/b、b/c和a/c分别对应于球形坐标中的x-y、y-z、x-z平面。椭球半轴长度随应变的变化见图5.55。半轴长度的变化表示该方向上接触数目的变化。

首先对不同荷载条件下接触方向的分布进行总体分析可以看出，初始状态下，所有试样接触方向的分布都比较均匀（球形柱状图接近于球形）。当剪应变较大时（10%），平面应变试样和三轴压缩试样接触方向分布近似于花生形，而直剪试样接触方向分布近似于南瓜形且有一定角度的倾斜。

对于平面应变试样，在初始状态下，竖向和水平向的接触方向分布都比较均匀。当试样受剪后，竖直方向（第一主应力方向）的接触开始增加。水平平面上，第二主应力方向的接触增加，而第三主应力方向的接触减少。从图5.55（a）可以看出，a、c增加，b减少。从图5.55所示的a、b、c的变化曲线可以看出，c的曲线形状与第4章讨论的应力—应变曲线非常相似。也就是说，对于松散试样，c一直增加，而对于密实、中密试样，刚开始加载时c增加，当应变大于2%～4%之间某一值时，c开始减小。这一现象被认为是偏应力的增加和试样细观结构变化所导致的。当偏应力达到最大值之前，第一主应力方向的接触增加，也就是Oda和Kazama（1998）提出的柱状构造开始发展。在柱状构造发展的过程中，第三主应力方向的接触减少，这与图5.55中b值减小相一致。Sitharam等（2002）同样观察到第三主应力方向接触减少，而第一主应力方向的接触增加。当偏应力达到最大值后，试样开始进入软化阶段。柱状结构开始破坏，这就导致了第一主应力方向的接触开始减少。对于松散试样，因为没有柱状结构形成阶段也没有软化阶段，所以第一主应力方向的接触一直增加。另外一个值得注意的现象是参数a的曲线形状与参数c相似，这与第4章讨论过的第一主应力和第二主应力方向的应力—应变曲线非常相似的现象完全一致。

对于三轴压缩试验条件，密实试样和松散试样接触方向分布如图5.50和图5.51所示。与平面应变试验相似，在初始状态下，竖向和水平向的接触方向分布都比较均匀。随着加载的进行，竖直方向的接触越来越多，水平方向的接触越来越少。从图5.55（b）中也可以看出，随着轴应变增加，c增加而a、b减少。在试样受剪的过程中，第一主应力方向的接触越来越多，第三主应力（拉力）方向的接触越来越少。因为三轴压缩试样为扩散或鼓胀破坏，所以没有剪切带和柱状结构形成。所以参数c一直增加，没有减少。因为试样是轴对称的，所以在抗剪的过程中水平面上接触方向分布一直比较均匀。当应变较大时，接触方向分布为花生形，如图5.50和图5.51所示。这与其他学者的结论相一致（Rothenburg and Bathurst，1989；Ouadfel and Rothenburg，2001）。

直剪条件下密实试样和松散试样的接触方向分布见图5.52和图5.53。在初始状态下，接触方向均匀分布。当试样受剪后，接触方向分布开始向花生形变化。值得注意的是，与平面应变条件和三轴压缩条件不同，直剪条件下椭球的半轴不再沿竖直或者水平方向，而是有一定角度的倾斜。这是一个重要的现象，说明在直剪条件下，某一个特定角度方向的接触变多。这一特定角度方向的接触的增加与法向力和切向力的分布有关，与主应力轴方向的旋转有关，这些内容会在后面加以讨论。

图5.48　平面应变条件下密实试样（PS-D75）接触方向分布图

图5.49　平面应变条件下松散试样（PS-L75）接触方向分布图

图5.50　三轴压缩条件下密实试样（CTC-D75）接触方向分布图

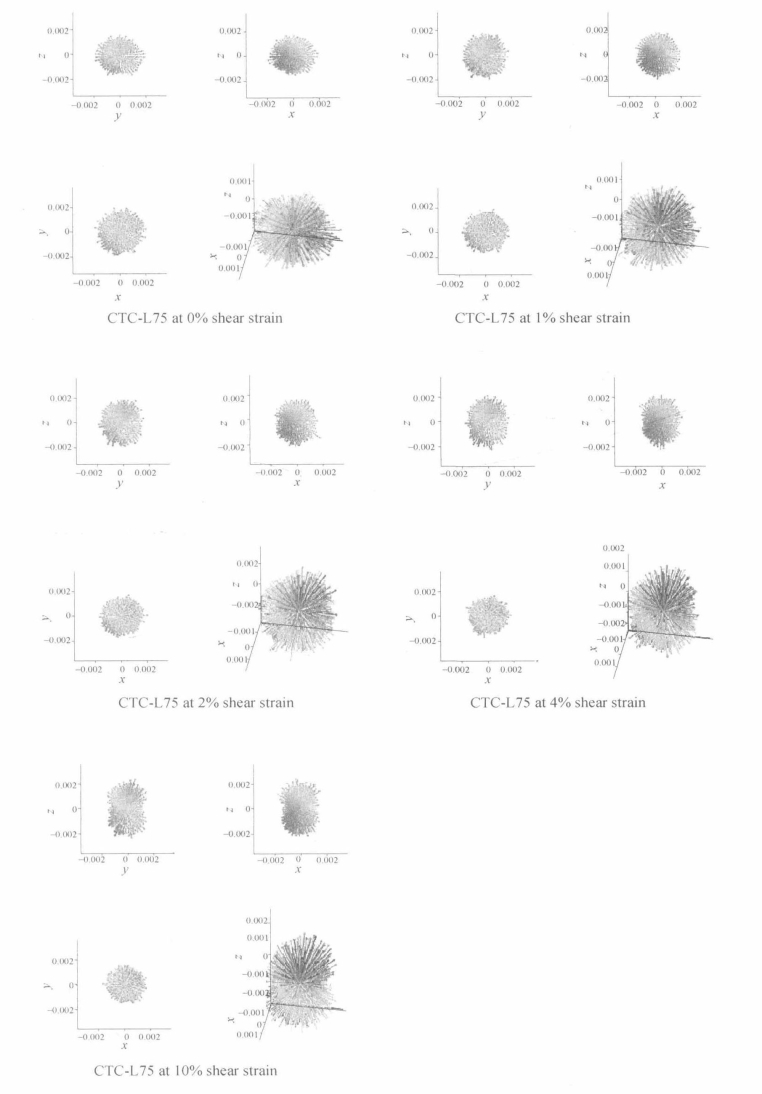
图5.51　三轴压缩条件下松散试样（CTC-L75）接触方向分布图

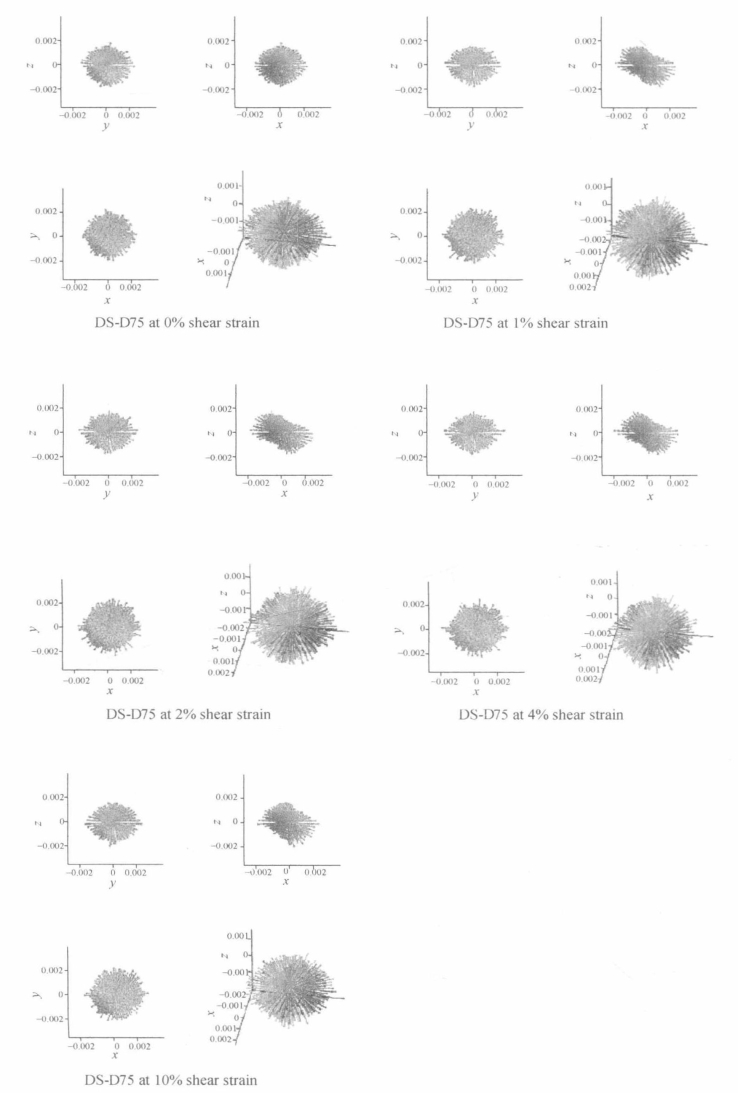
图5.52　直剪条件下密实试样（DS-D75）接触方向分布图

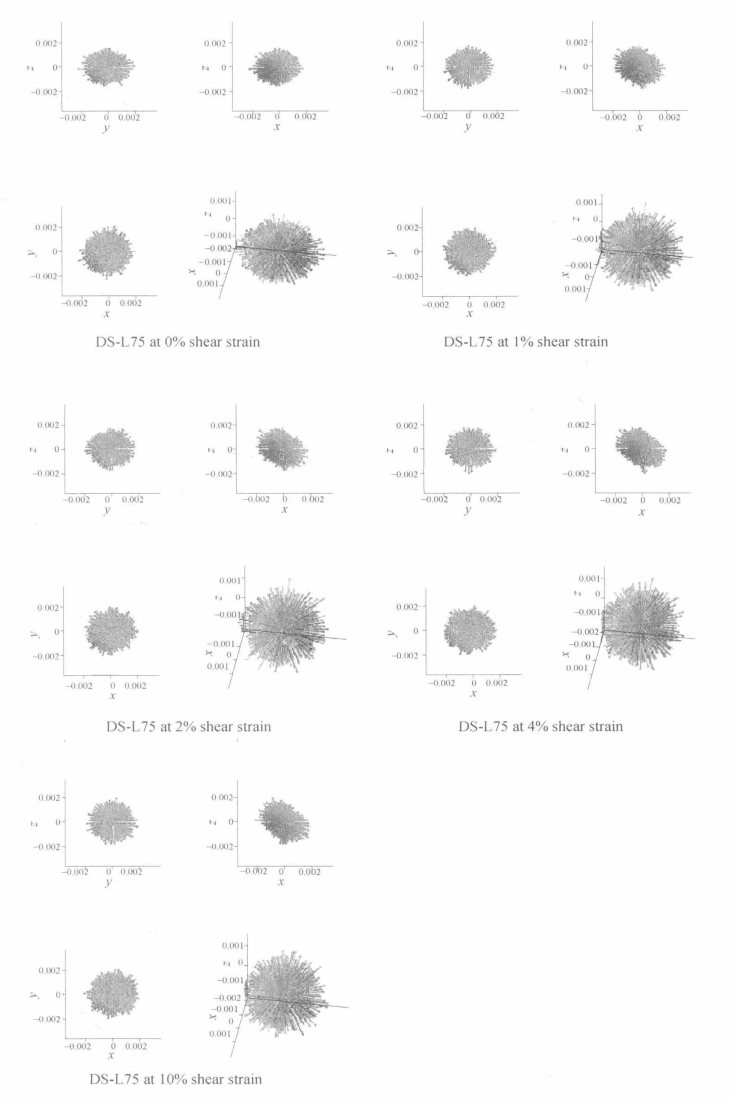
图5.53　直剪条件下松散试样（DS-L75）接触方向分布图

图5.54　接触方向分布图拟合椭圆半轴比

（a）平面应变试样；（b）三轴压缩试样；（c）直剪试样

图5.55　接触方向分布图拟合椭圆半轴长

（a）平面应变试样；（b）三轴压缩试样；（c）直剪试样

5.4.3.3　法向接触力分布

与接触方向一样，离散元数值模拟可以很方便地获得每个接触点处的法向力。因为每一方向角度范围（立体角）内的接触数目可以通过上一节的内容确定，该方向所有接触的法向接触力之和除以接触数目便可得到该方向的平均法向接触力。以该平均法向接触力作为球形柱状图中的半径，便得到法向接触力的球形柱状分布图。

图5.56至图5.62所示为低围压下（75kPa）不同密实度的试样在不同荷载条件下的法向接触力的球形柱状分布图。每个图包括三个垂直于不同坐标轴的平面投影图和一个三维立体图。拟合球形柱状图的椭球的半轴比a/b、b/c、a/c以及椭球半轴长a、b、c如图5.62和图5.63所示，通过这些参数研究法向接触力的分布特性。

首先，所有试样在初始状态下法向接触力分布图基本为球形。图5.62中a/b、b/c、a/c在应变为0时都近似等于1，说明在初始状态下，试样均匀且各方向平均法向接触力相等。

在平面应变条件下，无论是密实试样还是松散试样，受剪后法向接触力分布从球形变化为花生形，且长轴方向与第一主应力方向一致。这与之前一些学者的结论一致（Ouadfel and Rothenburg，2001；Sitharam et al.，2002）。但是，松散试样和密实试样法向接触力分布的变化过程并不一样。对密实试样，从图5.56可以看出，应变在0～2%之间时，花生状分布图的长轴（大主应力方向）一直在变长，之后开始变短。这可以从图5.63（a）更清楚地看出，当应变低于1%～2%之间某一值时，c值一直变大，但当应变达到约4%时，c开始减小。与密实试样不同，松散试样在受剪的过程中竖向法向接触力分布图的轴长度一直增加。这可以从法向接触力的柱状图5.57和椭球长轴变化图5.63（a）看出。在图5.63（a）中，松散试样的c值在整个受剪过程中一直增加。试样法向接触力的分布反映了试样的宏观应力—应变特性。对于密实试样，在破坏前或硬化阶段，偏应力增加。当偏应力达到最大值后，试样进入软化阶段，偏应力开始减小。但对于松散试样，偏应力一直增加，没有软化阶段。这些性质都可以从法向接触力分布图以及椭球长轴长度c的变化上看出来。另一个重要现象是水平面上法向接触力分布的变化，这与试样第二主应力的影响有关。椭球半轴a（与第二主应力相对应）的变化与c（与第一主应力相对应）相似。这一结论再次验证了第4章中第二主应力与第一主应力具有相似的应力—应变特性的结论。

三轴压缩条件下，试样在初始状态下的法向接触力的分布也比较均匀。试样受剪后，法向接触力的球形柱状分布图在竖向（第一主应力方向）的变化与平面应变试样相似。密实试样椭球的竖直方向半轴长度先增加后减小，而松散试样的竖向半轴一直增加。这与三轴压缩试样的应力—应变特性相一致。与平面应变试样不同，三轴压缩试样具有轴对称性，所以在试样抗剪过程中，水平方向的法向接触力分布始终基本均匀。这可以从图5.58和图5.59中看出，图中x-y面的分布图一直近似于圆形，且图5.62（b）中a/b的值一直近似于1。

对于直剪试样，初始状态下，法向接触力的分布同样是比较均匀的。当试样受剪后，法向接触力分布图从球形开始向花生形转变，且法向接触力分布图的轴方向开始有所倾斜。这与上一节中接触方向分布图中的变化相似，也与Masson和Martinez（2001）和Zhang和Thornton（2007）的二维离散元模拟结论相一致，他们发现直剪试样在临界状态下主应力和主应变的方向共轴，并与水平方向成45°角。将法向接触力分布图与接触方向的分布图相比较，发现轴偏转几乎一致。这是因为在每个接触点处的法向力和该接触点的方向量本来就是一致的。在实验室直剪试验中，也观察到了主应力轴旋转这一重要现象（Rowe et al.，1964；Roscoe et al.，1967），但是还没有人从细观层面，通过接触力来证实主应力轴旋转。法向接触力分布与接触方向分布发生一致偏转，说明直剪试样受剪后第一主应力方向的接触增多。数值模拟很好地再现直剪试样中主应力轴旋转这一重要现象，说明本书数值模型的建立是合理正确的，从而可以从宏细观不同角度正确反映颗粒材料的行为特性。(www.xing528.com)

图5.56　平面应变条件下密实试样（PS-D75）法向接触力分布图

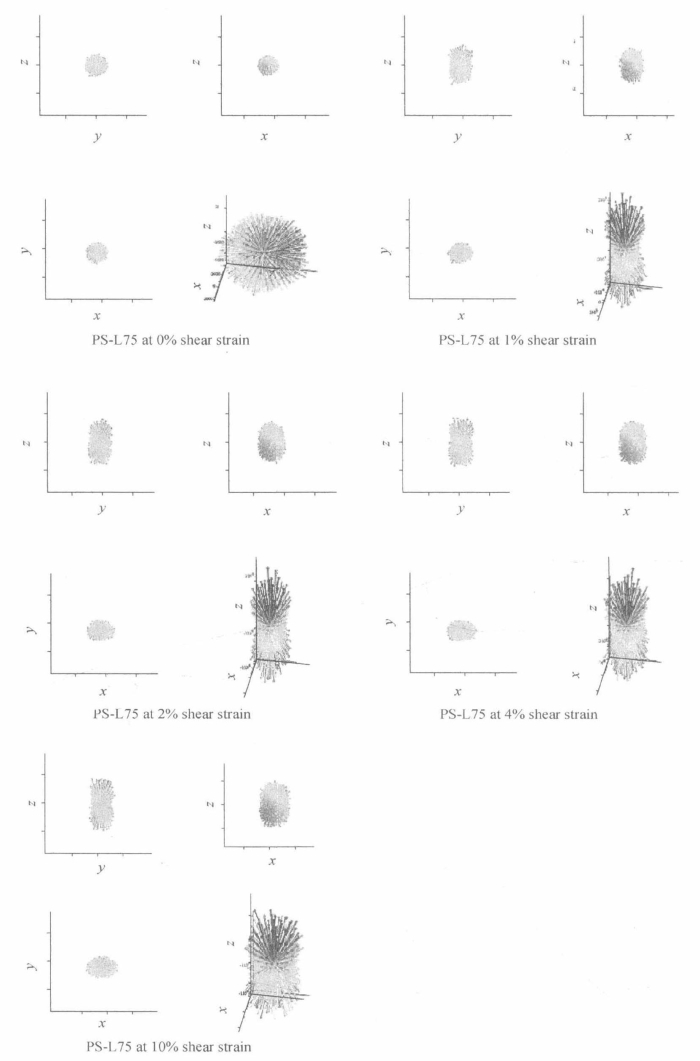
图5.57　平面应变条件下松散试样（PS-L75）法向接触力分布图

图5.58　三轴压缩条件下密实试样（CTC-D75）法向接触力分布图

图5.59　三轴压缩条件下松散试样（CTC-L75）法向接触力分布图

图5.60　直剪条件下密实试样（DS-D75）法向接触力分布图

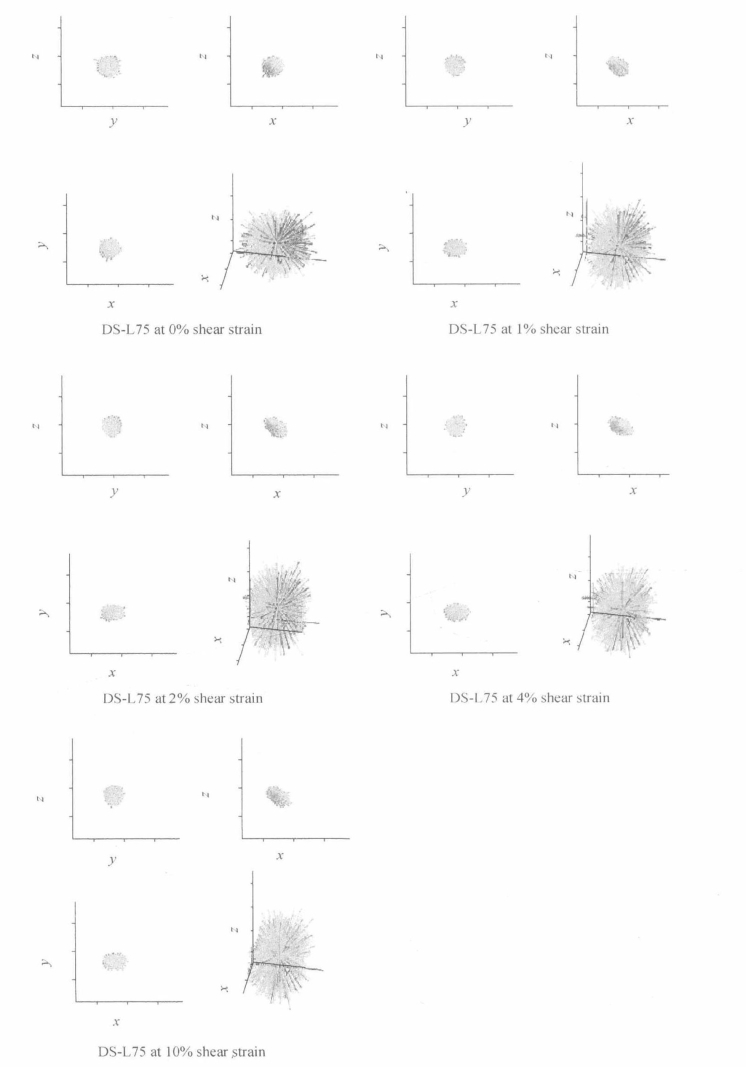
图5.61　直剪条件下松散试样（DS-L75）法向接触力分布图

图5.62　法向接触力分布图拟合椭圆半轴比

（a）平面应变；（b）三轴压缩；（c）直剪

图5.63　法向接触力分布图拟合椭圆半轴长

（a）平面应变；（b）三轴压缩；（c）直剪

5.4.3.4　切向接触力分布

采用与法向接触力分布相同的分析方法，对切向接触力的分布特点进行研究。图5.64至图5.69所示为低围压下（75kPa）不同密实度的试样在不同荷载条件下切向接触力的球形柱状分布图。拟合椭球的半轴比a/b、b/c、a/c以及椭球半轴长a、b、c如图5.70和图5.71所示。

图5.64　平面应变条件下密实试样（PS-D75）切向接触力分布图

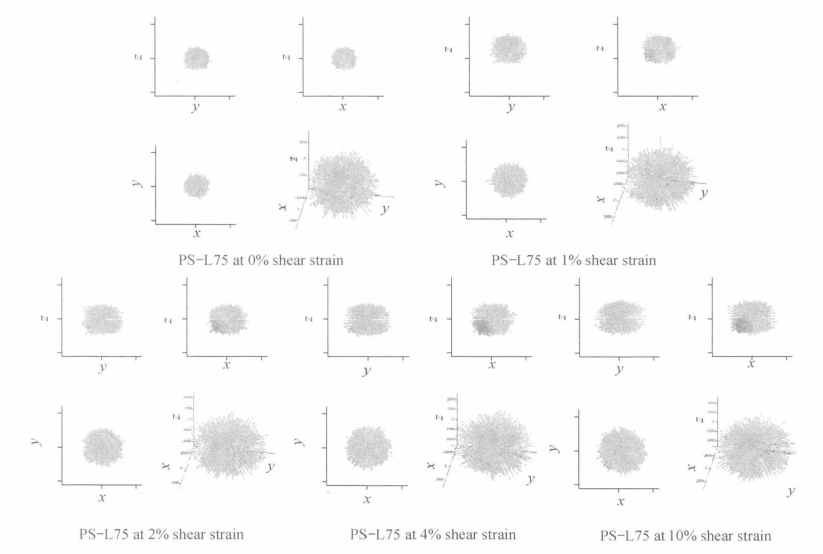
图5.65　平面应变条件下松散试样（PS-L75）切向接触力分布图

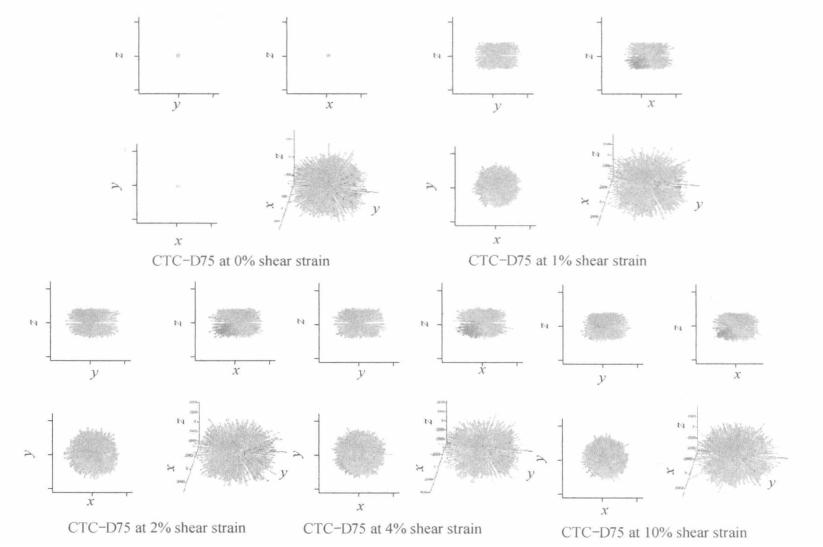
图5.66　三轴压缩条件下密实试样（CTC-D75）切向接触力分布图

图5.67　三轴压缩条件下松散试样（CTC-L75）切向接触力分布图

图5.68　直剪条件下密实试样（DS-D75）切向接触力分布图

图5.69　直剪条件下松散试样（DS-L75）切向接触力分布图

图5.70　切向接触力分布图拟合椭圆半轴比

（a）平面应变；（b）三轴压缩；（c）直剪

图5.71　切向接触力分布图拟合椭圆半轴长

（a）平面应变；（b）三轴压缩；（c）直剪

首先分析试样在初始状态下切向接触力的分布。从图中可以发现，当应变为0时，平面应变、三轴压缩、直剪试样的切向力都很小。通过比较可知，松散试样的切向力相对比较大一点，这可能是由于生成颗粒时摩擦系数不同导致的。第3章中提出，为了生成不同密实度的试样，在生成颗粒时给颗粒赋予不同的摩擦系数。将密实试样的颗粒摩擦系数在生成时设为0，将松散试样的颗粒摩擦系数设置为很大。虽然颗粒摩擦系数在试样生成后会设置为真实大小，但因为松散试样在生成时的摩擦系数比密实试样高，所以松散试样中还是会形成比密实试样大的咬合切向力。

其次，对应变较大时平面应变、三轴压缩试样切向接触力的分布进行总体比较分析。从图中可以看出，无论是平面应变试样还是三轴压缩试样，当试样受剪后，切向力柱状分布图变为南瓜形。这与之前的一些二维数值模型（Rothenburg and Bathurst，1989）和三维立方体数值模型（Ouadfel and Rothenburg，2001；Sitharam et al.，2002）的结论不一致。之前的研究采用傅里叶拟合法和调和函数分析切向力分布，研究结果是在应变较高时切向力的分布呈哑铃形。造成这一差别的原因有很多，如模型维度的不同、试样形状不同、加载方案不同、拟合方法不同等。

第三，直剪试样切向接触力分布图的坐标轴同样与初始定义的坐标轴方向不同，坐标轴发生旋转。前一节曾提到过，法向接触力分布图的旋转角度与接触方向分布图的旋转角度非常接近。但是将图5.68和图5.69与图5.52和图5.53相比较可以发现，切向接触力分布图的轴方向近似垂直于法向接触力分布图的轴方向。这同样证实了直剪条件下试样主应力发生旋转的现象。

第四，结果发现，平面应变和三轴压缩条件下，法向接触力分布图拟合的椭球半轴长a、b、c随应变的变化规律与第4章讨论的应力—应变关系曲线一致，即在三个主应力方向上，密实试样和中密试样的切向力都是先增加后减小，但是松散试样切向力一直增加，没有减小。