砂性土颗粒方向分布图分析

如前所述，数值模型中的颗粒采用两个球形重叠而成宽高比为1.5∶1的块颗粒。离散元数值模拟中，组成每个块颗粒的两个球可以识别，任意时刻每个球的位置和半径可以确定。如果组成块颗粒两个球的质心分别为（x1，y1，z1）和（x2，y2，z2），且半径相等，都为r，那么块颗粒方向就可以确定。两个球颗粒之间的距离可以通过下式计算而得：

对宽高比为1.5∶1的块颗粒，D=r。

在如图5.38所示的球形坐标系中，块颗粒的方向可以通过θ和φ两个角度来表示：

求出每个颗粒方向后，可以用球形柱状分布图表示试样内颗粒方向的分布。采用Leopardi（2006）提出的递归等面积球形分区法对单元球体进行分区。用块颗粒方向位于每一立体角（Solid Angle）方向范围内的颗粒数占总颗粒的百分数表示球形柱状图中该立体角方向的半径，就可以得到试样中颗粒方向分布的球形柱状分布图。

通过球形柱状图，对密实试样在低围压下（75kPa）不同剪应变状态时的颗粒方向分布进行研究。图5.39和图5.40是平面应变条件，图5.41和图5.42是三轴压缩条件，图5.43和图5.44是直剪条件。每种荷载条件都用三个垂直于坐标轴的投影平面图和一个三维立体图来显示。y-z平面图和x-z平面图表示的是竖直投影面上颗粒方向分布，x-y平面表示的是水平投影面上颗粒方向分布。

对图5.39至图5.44用椭球来进行数据拟合，用标量分析的方法来表示颗粒主要分布方向。假设椭球轴与坐标系重合，那么椭球的公式为

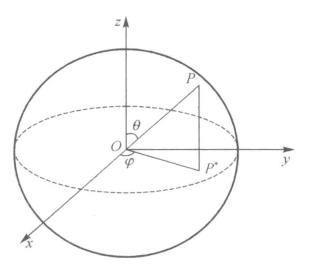
图5.38　球形坐标系定义

式中，a、b、c分别为椭球半轴的长度。这个假设可以通过分析矩阵hTh的特征值来进行验证，其中h为柱状图中每个柱数值的x、y和z分量（这种方法与主分量分析方法一致，相当于计算协方差矩阵的特征值）。另外一种相对不太严格但性质相同的方法是用一个广义椭球体（即不忽略截项的椭球体）进行数据拟合。使用上述两种方法发现，简化椭球与广义椭球的拟合基本一致。各向异性程度的定量化分析的最简单方法是计算椭球的半轴比。图5.45（a）、（b）、（c）所示分别为平面应变、三轴压缩、直剪条件下的颗粒分布拟合椭球的半轴比。a/b、b/c和a/c分别对应于球形柱状图中的x-y、y-z、x-z平面。椭球半轴长度随轴应变的变化如图5.46所示，其中a、b、c分别为第二、第三、第一主应力的方向椭球半轴长度。

首先，对不同荷载条件下颗粒方向分布的总体分析可以发现，颗粒方向的分布与试样密度和荷载条件都有关系。在平面应变和三轴压缩条件下，应变较大时，密实试样颗粒方向分布图为南瓜形，而松散试样颗粒方向分布图为花生形。直剪条件下，松散试样和密实试样的颗粒方向分布图都为花生形。

平面应变条件下，如图5.39和图5.40所示，试样在初始状态下，竖直颗粒比水平颗粒多，松散试样这一现象比密实试样更加明显。在水平面上，颗粒方向分布比较均匀（x-y平面分布近似为圆形）。这与图5.45（a）所示一致，图中初始状态下b/c和a/c小于1，a/b约为1。随着加载的进行，竖直颗粒的数目减少，即图5.46（a）中的c值减小。在水平面，也就是垂直于第一主应力的平面上，颗粒方向分布从均匀变为不均匀。多数颗粒的方向变为第三主应力方向，这也可以从图5.46（a）中看出，图中b随着应变增加而增加。在剪切过程中，第二主应力方向的颗粒数目变化不大（a随着应变改变变化不大）。

图5.39　平面应变条件下密实试样（PS-D75）颗粒方向球形柱状分布图

(www.xing528.com)

图5.40　平面应变条件下松散试样（PS-L75）颗粒方向球形柱状分布图

图5.41　三轴压缩条件下密实试样（CTC-D75）颗粒方向球形柱状分布图

图5.42　三轴压缩条件下松散试样（CTC-L75）颗粒方向球形柱状分布图

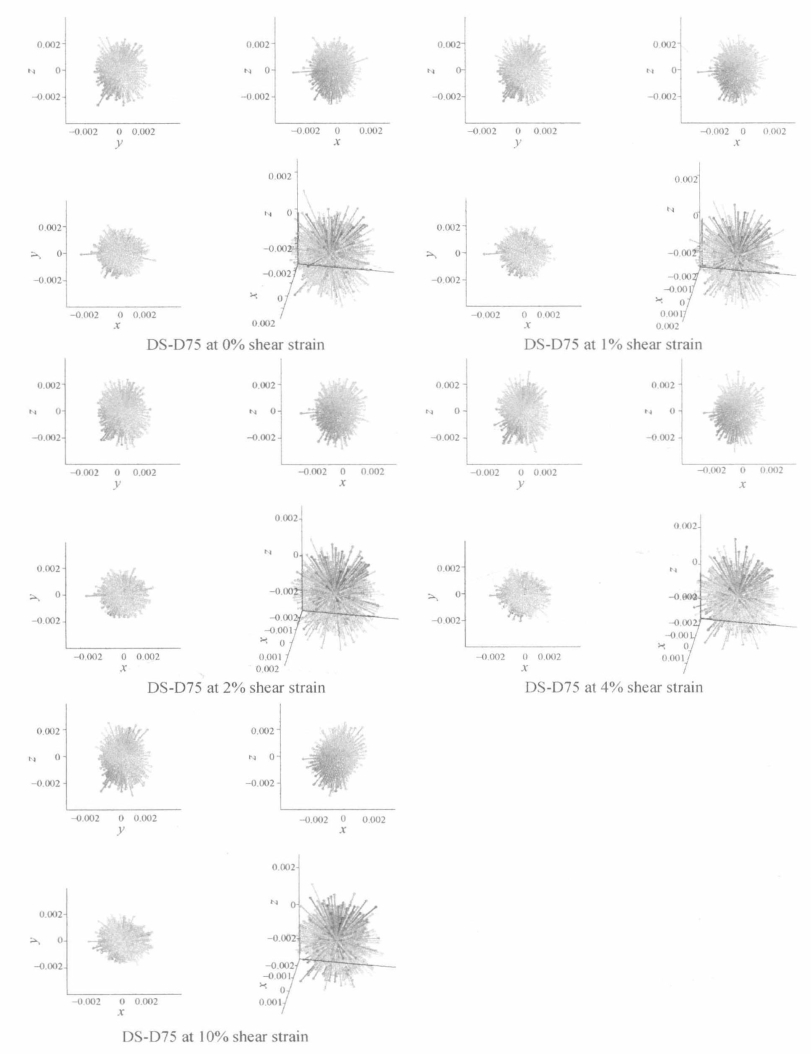
图5.43　直剪条件下密实试样（DS-D75）颗粒方向球形柱状分布图

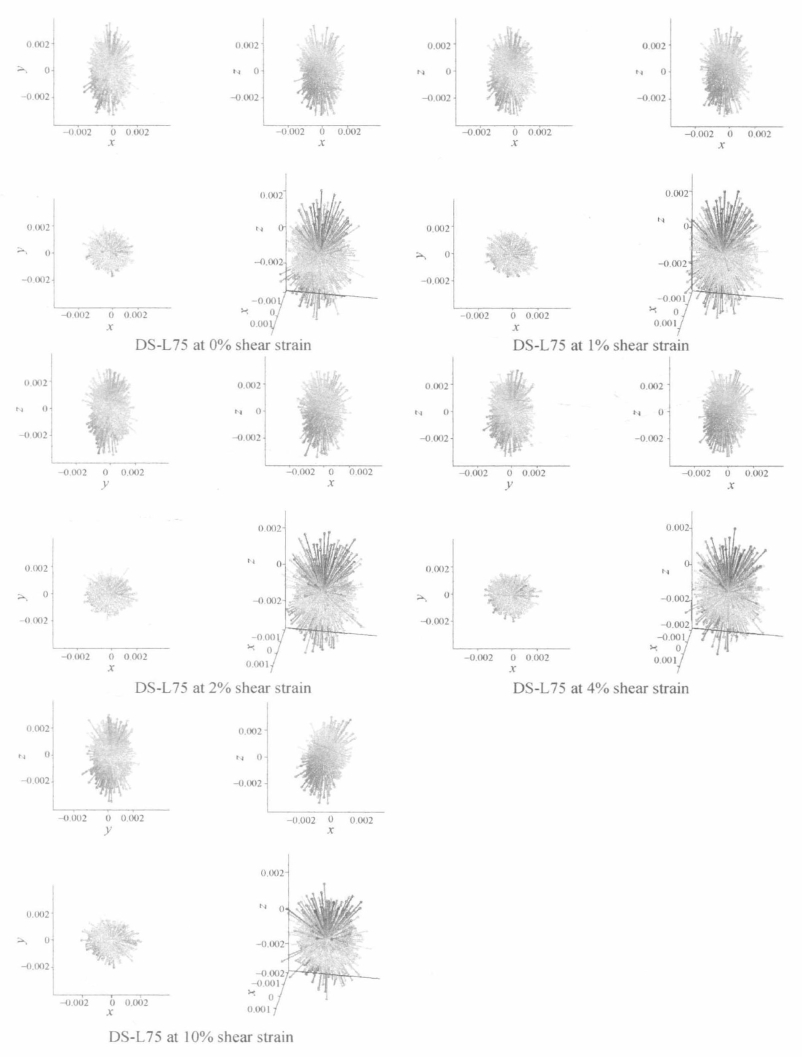
图5.44　直剪条件下松散试样（DS-L75）颗粒方向球形柱状分布图

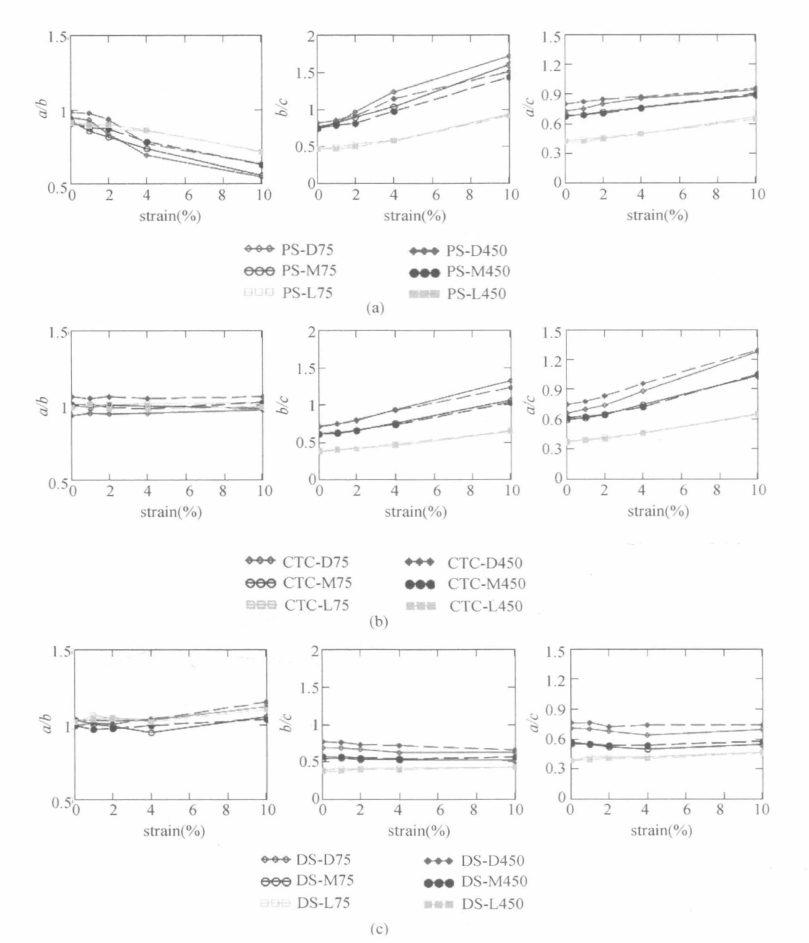
图5.45　颗粒方向分布图拟合椭圆半轴比

（a）平面应变；（b）三轴压缩；（c）直剪

图5.46　颗粒方向分布图拟合椭圆半轴长

（a）平面应变；（b）三轴压缩；（c）直剪

三轴压缩条件下，如图5.41和图5.42所示，在水平面（x-y面）上，也就是与第一主应力垂直面上，试样颗粒方向分布比较均匀。而且在整个加载过程中，水平面上的颗粒方向基本保持均匀分布。这也可以从图5.45（b）看出，图中a/b基本接近于1。在初始状态下，竖向颗粒比水平颗粒多，这与应变为0时b/c和a/c小于1相一致。随着剪切进行，竖向颗粒越来越少，对应于图5.46（b）中的c越来越小。相应地，水平颗粒越来越多，图5.46（b）中的a、b随着加载进行越来越大，且a、b增加速度基本一致，从而使得在水平面上颗粒方向分布一直比较均匀。

图5.43和图5.44所示为直剪试样颗粒方向分布。在初始状态下，与平面应变试样和三轴压缩试样一致，竖向颗粒比水平颗粒多，且试样密度越低越明显。当试样受剪时，颗粒方向分布仅有微小变化。但是在材料抗剪过程中，剪切面或破坏面上颗粒方向分布变化较大。造成试样整体颗粒方向分布变化较小的原因可能是由于剪切面或破坏面上颗粒的数目比较少，所以不足以引起试样总体颗粒方向分布发生较大变化。虽然剪切可以引起剪切面上颗粒旋转，对单独颗粒方向的影响较大，但是对整体颗粒方向的分布影响较小。由于椭球体轴与坐标轴一致的假设并不成立，所以在直剪条件下a/b、b/c、a/c、a、b、c没有意义。