颗粒旋转是应变局部化现象的一个特征-数值分析研究

5.3.1.1　前期工作

在实验室试验（Oda and Kazama，1998）和数值模拟研究（Bardet and Proubet，1991）中都观察到试样在荷载作用下的内部颗粒发生旋转的现象。研究颗粒旋转对材料行为特性影响的方法有很多，包括理论分析法（Bardet and Proubet，1991）、试验法（Wang et al.，2004）、数值模拟法（Iwashita and Oda，1998）等。

Oda和Kazama（1998）采用X射线断层图像法进行研究，他们使用显微镜和薄切片光学测量平面应变条件下试样的细观结构变化。研究发现，剪切带边界的颗粒旋转较大，说明在很窄的区域内颗粒旋转差距很大，颗粒旋转的方向与试样连续介质意义上的宏观旋转相平行。颗粒的转动阻力被认为是颗粒土材料强度的一个非常重要的组成部分。Wang等（2004）提出了一种采用X射线断层图像法对试样中的颗粒进行三维重构的方法。试样中的颗粒由其质心坐标和形态特征表示，通过这种方法，每个颗粒的平动和转动都能表示出来。

尽管有很多学者采用试验法来研究颗粒旋转，但是这些试验一般都非常复杂，不易于操作。由于数值模拟方法相较于试验法简单经济，所以被越来越多的学者用来对颗粒旋转进行研究。

Bardet（1994）研究了理想颗粒土中颗粒旋转对破坏的影响。研究发现，颗粒旋转对材料弹性性能的影响微乎其微，但是对材料剪切强度的影响非常大。试样颗粒的总体平均旋转很小，但是剪切带内颗粒的平均旋转很大。由于颗粒的旋转主要集中在剪切带内，所以试样的整体摩擦和残余摩擦比剪切带内颗粒间摩擦小。为了考虑接触点处颗粒转动的影响，Iwashita和Oda（2000）提出了一种修正离散元法（MDEM）。在修正离散元法中，为了考虑转动阻力的影响，在每一个接触点处增加了一个弹簧、一个缓冲器、一个没有拉力的连接以及一个滑块。采用这个模型，他们观察到了与实验室结论（Oda and Kazama，1998）以及其他数值模拟结果（Bardet and Proubet，1991）一致的现象，即剪切带边界处颗粒旋转梯度很大。Masson和Martinez（2001）用离散单元法模拟了一系列的直剪试验，对松散试样和密实试样中颗粒的旋转进行了分析。结果表明，颗粒旋转是应变局部化现象的一个特征。O'Sullivan和Bray（2004）提出了使用中心差分时间积分法来确定离散元模型合理时间步的方法。研究发现，无论在二维模型还是三维模型中，颗粒是否发生旋转对临界时间步的影响都很大。如果允许颗粒旋转，临界时间步长会比较小。Suiker和Fleck（2004）研究了颗粒旋转对三维离散元模型强度、体积变化以及破坏特性的影响。他们模拟了两种情况，一种允许颗粒旋转，另一种不允许颗粒旋转。模拟结果显示，阻止颗粒旋转可以使材料的偏应力强度提高两到三倍，同时会使材料破坏提前（更小应变时发生破坏）。当颗粒旋转被限制时，临界配位数减少，孔隙比变大，说明颗粒旋转会引起更大的剪切膨胀。Powrie等（2005）模拟了一系列三维的平面应变试验，通过颗粒旋转来分析一些因素如载荷板摩擦、初始试样孔隙比、颗粒形状以及颗粒间摩擦角等对应变局部化的影响，通过颗粒旋转来研究材料变形机理。Jiang等（2005）提出了一种考虑土颗粒旋转阻力的二维离散模型。在这种模型中，接触点处的位移被分为纯滑动位移和纯滚动位移两个分量。通过将模型中颗粒接触从点接触改为具有一定宽度的面接触，引入了一个新的参数——形状参数。结果表明，使用该模型的模拟结果与试验结果更为接近。

5.3.1.2　颗粒旋转分布图

数值模拟中，模型颗粒采用由两个球重叠而成的块颗粒，块颗粒宽高比为1.5∶1。颗粒摩擦系数根据物理试验（Proctor and Barton，1974）结果取为0.31。通过采用非球体块颗粒，避免了球颗粒旋转过大的问题，与真实情况更为贴近。

为了能清楚方便地表示颗粒旋转分布，与材料的孔隙比和配位数分析时选择的中心平面一样，平面应变试验采用与第二主应力方向垂直的中心位置平面，三轴压缩试验采用通过圆柱轴线的竖直平面，直剪试验采用沿着剪切方向但垂直于剪切带的中心平面，选择颗粒球心位于或靠近该中心面的颗粒，并用这些颗粒的旋转代表整个试样的颗粒旋转特性。图5.23、图5.24、图5.25分别为平面应变、三轴压缩、直剪条件下最终状态时颗粒旋转图。不同灰度表示颗粒旋转大小不同。

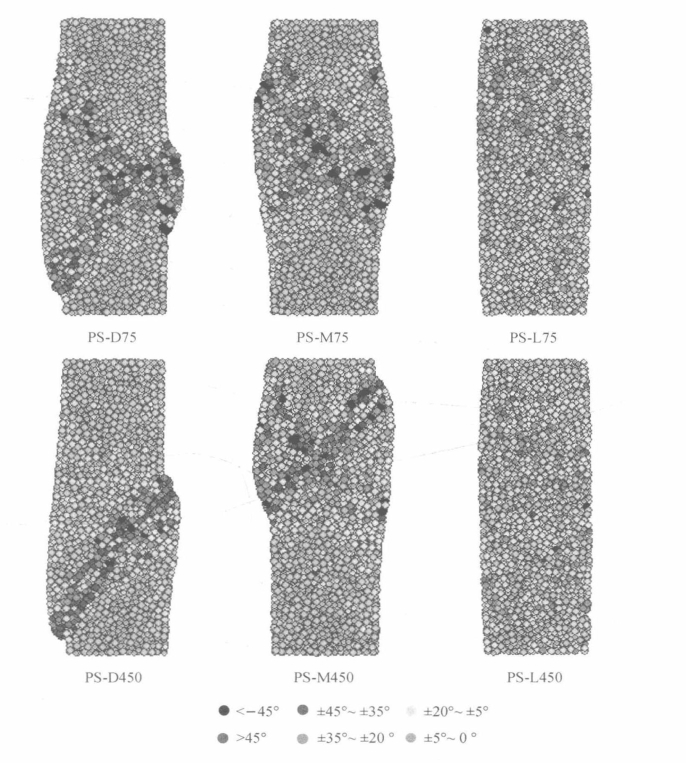
图5.23　平面应变试样最终状态颗粒旋转分布图

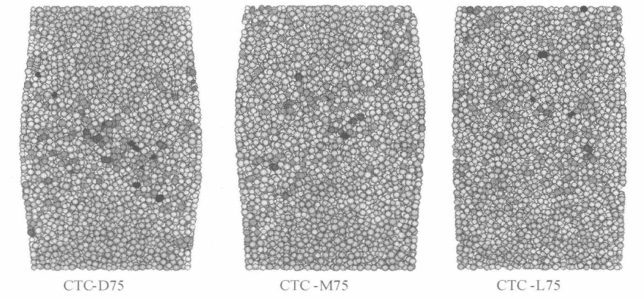
图5.24　三轴压缩试样最终状态颗粒旋转分布图

图5.25　直剪试样最终状态颗粒旋转分布图

从图5.23可以看出，平面应变条件下，不同密实度的试样具有不同的颗粒旋转特性。对于密实试样，颗粒旋转大的区域集中在一个窄的范围内，即剪切带内。高围压时，颗粒旋转图中只有一条明显的剪切带，而低围压时，有两条比较明显的剪切带。中密试样旋转较大的颗粒同样集中于代表剪切带的较窄区域，但它的集中现象不如密实试样那样明显。松散试样中没有出现明显的旋转较大的颗粒集中的现象，无论是高围压还是低围压下颗粒旋转都比较均匀。没有高旋转集中现象说明没有剪切带形成。

三轴压缩条件下（图5.24），密实试样中部颗粒旋转大于试样两端。但是旋转较大的颗粒并没有集中在一定区域内，说明没有形成明显的剪切带。进一步观察图5.24可以发现，在加载板附近存在两个锥形区。在这两个锥形区域内，颗粒旋转比较小，与前面讨论孔隙比时观察到的锥形区域一致。中密试样同样是中间的颗粒旋转较大，试样两端颗粒旋转比较均匀，在加载板附近同样可以观察到两个锥形区，但锥形区没有密实试样的锥形区明显。松散试样同平面应变试验中的观察比较一致，颗粒旋转比较均匀，没有出现集中区。

在直剪试验（图5.25）中，因为剪切面由试验设备决定，所以剪切面附近颗粒的旋转都比较大。无论是密实试样、中密试样还是松散试样，都可以观察到旋转较大颗粒集中于试样中部剪切带内。当竖向荷载相同时，密实试样剪切带厚度最小，中密试样次之，松散试样剪切带厚度最大。同样密实度而竖向荷载不同的试样，竖向荷载越大，剪切带厚度越小。(www.xing528.com)

从模拟结果可以发现，试样密实度越低，颗粒旋转越均匀，试样密实度越大，旋转较大的颗粒越容易集中在较窄的区域内。围压越大，旋转较大的颗粒越集中在较窄的区域内，围压越小颗粒旋转越均匀。

平面应变、三轴压缩、直剪最终状态时颗粒旋转云分布图分别如图5.26、图5.27、图5.28所示。

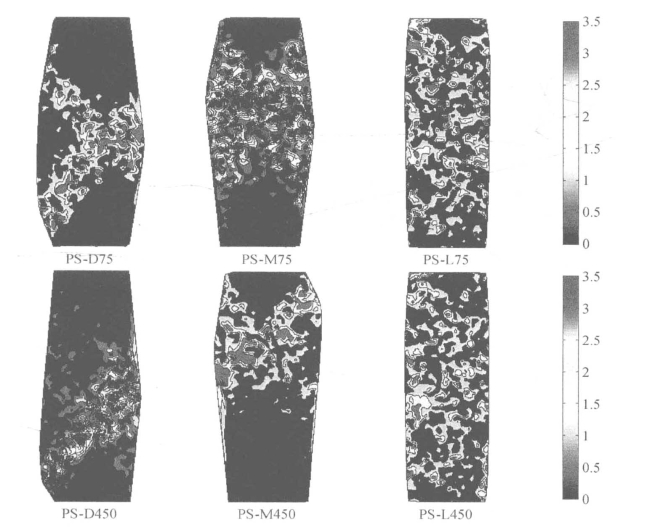
图5.26　平面应变试样最终状态颗粒旋转云图

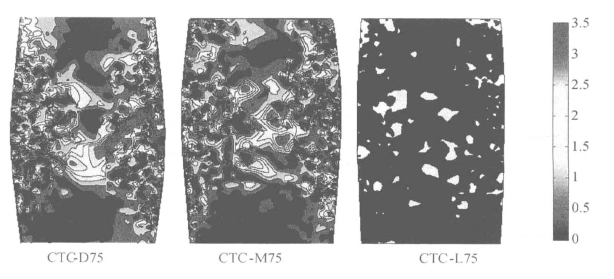
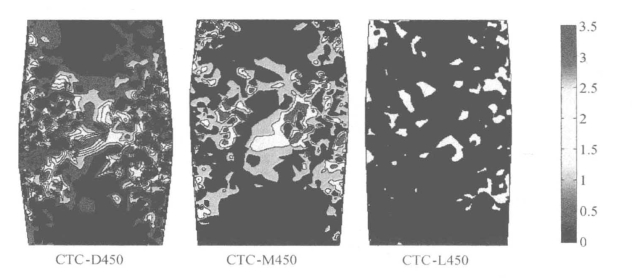
图5.27　三轴压缩试样最终状态颗粒旋转云图

图5.28　直剪试样最终状态颗粒旋转云图

5.3.1.3　颗粒旋转分布发展

从上面分析可以看出，颗粒旋转及其变化可以反映应变局部化的开展和变化，这与其他学者的发现相一致（Masson and Martinez，2001）。以高围压下密实试样在不同荷载条件下颗粒旋转的发展变化为例，图5.29、图5.30、图5.31所示分别为平面应变、三轴压缩、直剪试样颗粒旋转云图在加载过程中的变化。从这些图可以看出，平面应变和直剪试样在轴应变为3%～4%之间时出现应变局部化现象，在应变达到5%时，剪切带完全形成。这与之前通过孔隙比的分析得到的结论一致。

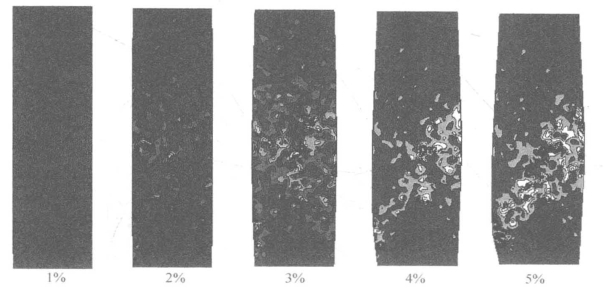
图5.29　平面应变试样（PS一D450）加载过程中颗粒旋转云图的变化

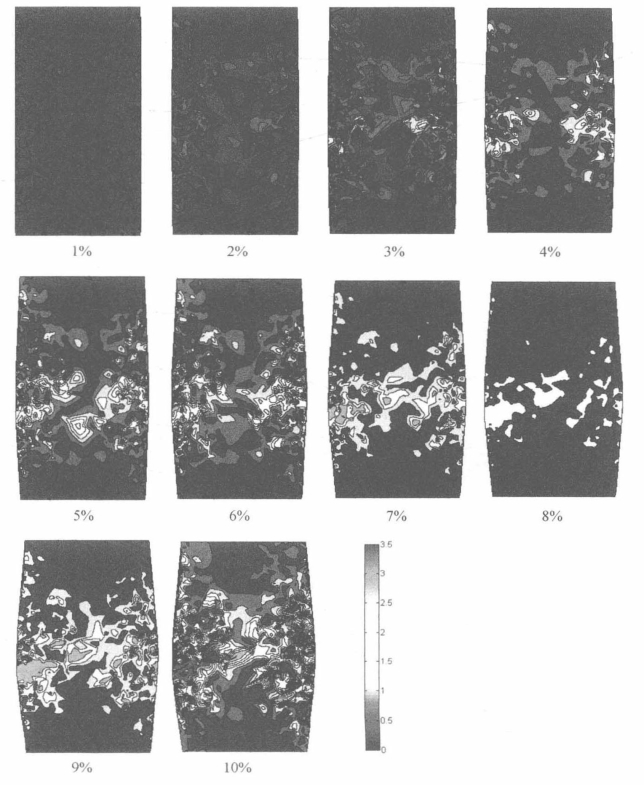
图5.30　三轴压缩试样（CTC-D450）加载过程中颗粒旋转云图的变化

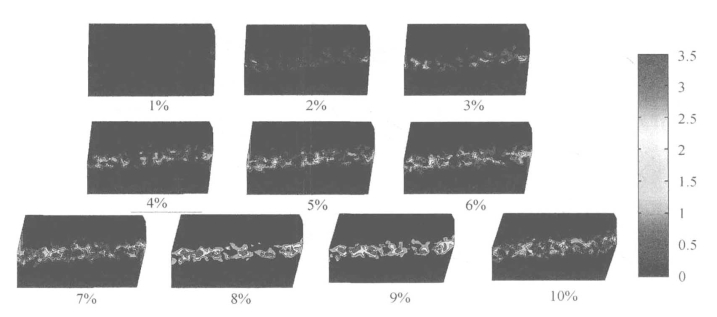
图5.31　直剪试样（DS-D450）加载过程中颗粒旋转云图的变化