岩土工程的很多问题都可以认为是小应变问题，但是在平面应变和三轴压缩条件下颗粒材料的小应变行为特性有很大的不同。实际应用中常使用三轴压缩试验数据来模拟平面应变条件，很少考虑颗粒材料在小应变时的两种荷载条件下的差异。如果离散元模型的建立正确合理，模型可以准确模拟和反映颗粒材料在小应变时的行为，那么模拟结果应该符合式（4.12）和式（4.13）。需要指出的是，上面提到的土体小应变时的反应与基于波的理论和方法测得的材料刚度有关。但在本节中，材料的弹性模量由轴向应变较小时（0.08%）计算得到，由于受荷后试样中的颗粒将发生微小的重分布，所以计算得到的这一弹性模量并不等于弹性模量真值。但在基于非波理论的室内试验和数值模拟中，所选的轴向应变需要考虑试验中的试样安置及材料的变形机理，所以这一轴向应变的大小应选择相对大一些。
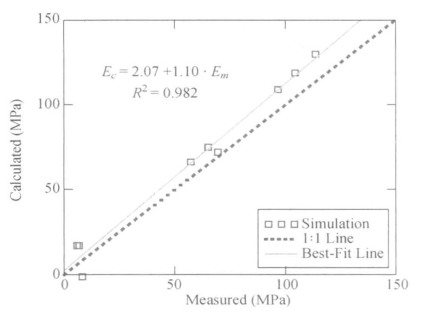
根据三轴压缩模拟计算出的小应变时的弹性参数与平面应变模拟中测得的参数值比较见图4.9和图4.10。从图中可以发现，根据三轴与平面应变关系理论计算所得的E和μ与数值模拟测量所得数据非常接近（靠近1∶1线），也就是说，数值模型中试样的小应变反应基本符合连续线弹性理论。但是，从图4.9仍可以发现，根据三轴与平面应变关系理论计算所得的平面应变试样的杨氏模量比数值模拟中直接测得的值高，这说明即使是小变形的情况下，颗粒材料也并非完全的线弹性材料。一般认为，计算Gmax时线性应变的阈值为3×10-4%，而研究所取的0.08%远大于该值。另外，三轴压缩试样变形后不再是标准的直立圆柱，平面应变试样变形后也不是正交长方体。总之，从图4.9和图4.10可知，数值模拟结果与式（4.12）和式（4.13）所给的理论关系不完全一致，但三轴压缩和平面应变试样在小应变时的行为特性还是具有一定相关性。
(www.xing528.com)
图4.9 平面应变试样杨氏模量的实测值与计算值（ε1=0.08%）
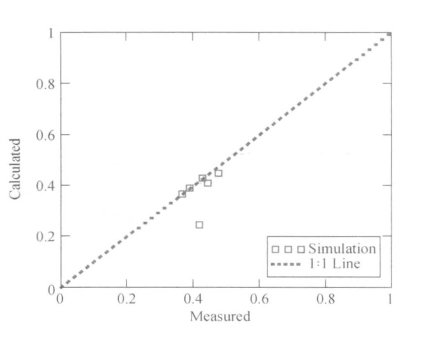
图4.10 平面应变试样泊松比的实测值与计算值（ε1=0.08%）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
