砂性土小应变特性分析研究

当土体应力或应变没有达到破坏条件，特别是应变很小时，通常把土体简化为线弹性材料。虽然实际上土体即使在小应变情况下也是非线性和非弹性的，但是通过简化的理想模型可以简单了解土的性能，从而对土的行为特性进行预测。Lee（1970）采用线弹性模型研究了三轴条件和平面应变条件的关系。

对理想各向同性弹性材料，三向主应变ε1，ε2，ε3可通过以下公式得出：

式中，E是杨氏弹性模量，μ是泊松比，σ1，σ2，σ3为三向主应力。

平面应变条件下，ε2=0，由上面公式可以推导出第二主应力和第一、第三主应力之间的关系：

将式（4.4）代入式（4.3）：

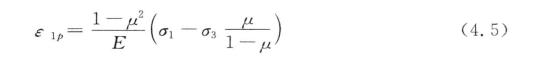
式（4.5）可以改写为：

式中：

(www.xing528.com)

可以证明，平面应变条件下的Ep和μp与一维条件中的E和μ具有相同的物理意义，所以，它们被看作是平面应变条件下的等效弹性模量和等效泊松比。以下下标中的p和t分别代表平面应变条件和三轴压缩条件。

体积应变表达式为：

在三轴压缩试验中，ε2=ε3且ε2=一μtε1。所以：

在平面应变试验中，体积应变表达式：

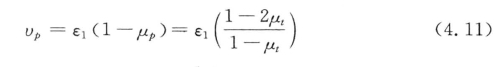
因此，平面应变条件和三轴压缩条件下土体性质参数关系可以表示为

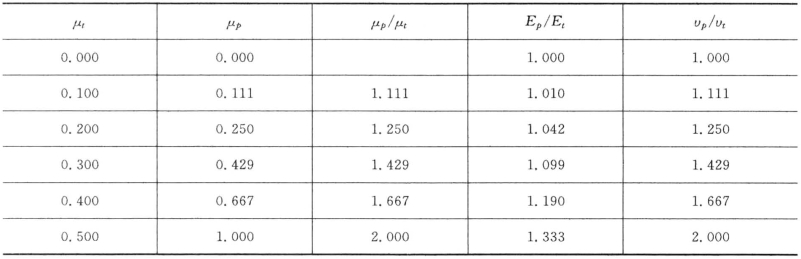
大部分弹性材料泊松比在0到0.5之间，所以平面应变的Ep，μp和υp分别比相应的三轴压缩试验的Et，μt和υt大，它们之间关系如表4.3所示。

表4.3　平面应变和三轴压缩试验的小应变弹性参数对比