模拟了9组平面应变试验、9组三轴压缩试验和9组直剪试验来研究不同荷载条件、不同围压、不同初始孔隙比时试验在不同应变状态的宏细观行为特性。对于平面应变和三轴压缩模拟试验，偏应力和平均应力根据剑桥方法定义为
式中，q为偏应力，p'为平均应力
分别为第一、第二、第三主应力（受压为正）。对于直剪试验，应力比是水平面上剪应力和竖向正应力的比值。图4.2、图4.3和图4.4分别是平面应变、三轴压缩和直剪数值模拟试验中偏应力或应力比以及体积应变与轴应变（ε1）的关系曲线。图4.5、图4.6和图4.7为平面应变、三轴压缩和直剪条件下摩擦角与膨胀角跟轴应变的关系曲线。数值模拟结果的部分主要数据在表4.2中列出。
表4.2 初始条件和部分主要试验结果
续表4.2
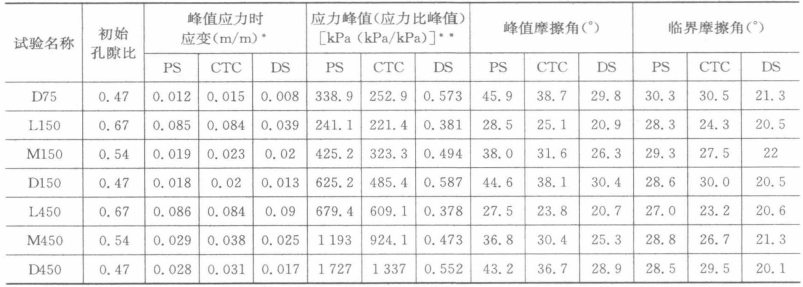
*：平面应变试验和三轴压缩试验为轴向应变，直剪试验为水平应变。
**：平面应变试验和三轴压缩试验为峰值偏应力，直剪试验为峰值应力比。
图4.2 平面应变试验偏应力和体积应变与轴应变的关系
图4.3 三轴压缩试验偏应力和体积应变与轴应变的关系
从图4.2到图4.4可以看出，密实试样具有明显的偏应力峰值或应力比峰值，且试样具有剪胀性，而松散试样没有明显的偏应力峰值或应力比峰值。这一结论与颗粒土的室内试验结果相一致（Cornforth，1964；Lee，1970）。图中显示，中密试样和密实试样在轴应变达到10%时还没有完全达到临界状态，虽然进一步施加荷载可以达到真正的临界状态，但是考虑到模拟时间，在轴应变达到10%时终止了试验。(www.xing528.com)
从表4.2可知，当试样具有明显的偏应力峰值时，平面应变试验达到偏应力峰值时对应的轴应变比三轴压缩试验小。这一结论与Cornforth（1964）和Lee（1970）的结论相一致。
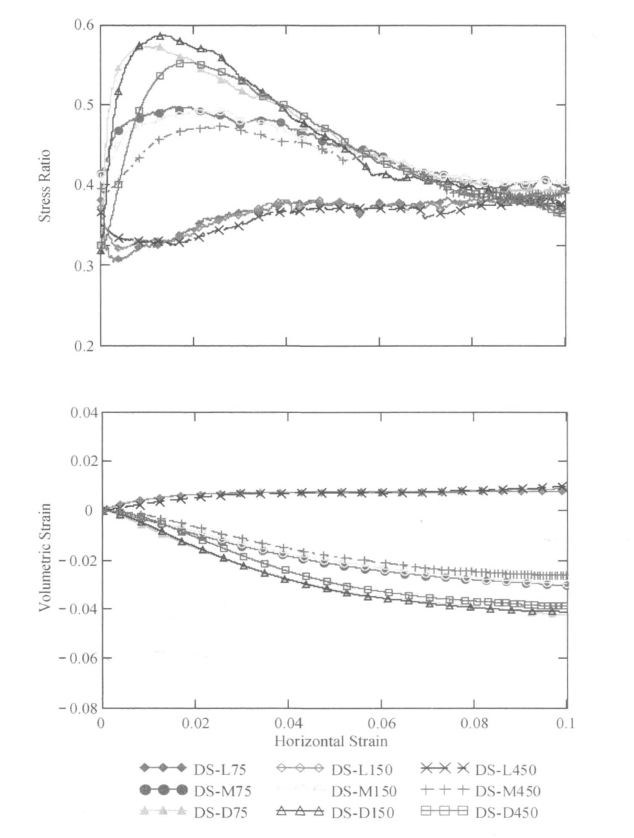
图4.4 直剪试验偏应力和体积应变与水平应变的关系
比较图4.2和图4.3可知，平面应变试验中密实试样的应变软化现象比三轴压缩试验更为明显，这与Peric等（1992）的理论分析以及Hettler和Vardoulakis（1984）的试验结果相一致。他们认为，对于三轴压缩条件，试样的应变软化主要受试样的不均匀性与加压板底部（摩擦约束）的影响，而与材料固有属性无关。本节中，所有的平面应变、三轴压缩、直剪试验，压板底部都设为光滑没有摩擦。在平面应变试验中，如果试样的破坏与剪切局部化同时发生，一般会出现明显的应变软化和体积变化，但在应变局部化形成后，软化和体积变化就会停止。
图4.5 平面应变试验摩擦角和膨胀角与轴应变的关系
进一步分析表4.2以及图4.2和图4.3可以发现，平面应变试样强度比同样孔隙比和围压大小下的三轴压缩试样强度大。平面应变试验中峰值摩擦角比对应三轴压缩试验中的峰值摩擦角大3.4°到7.2°。这与Lee（1970）的试验结果一致，Lee通过试验发现，平面应变试验的内摩擦角与三轴压缩试验的内摩擦角差值可能高达8°。表4.2中显示，直剪试验的峰值摩擦角比相应的平面应变和三轴压缩试验中的峰值摩擦角小。这与采用Rowe（1969）提出的直剪和平面应变峰值强度关系理论进行分析的结果相一致。图4.8比较了平面应变、三轴压缩、直剪试验的峰值摩擦角和临界摩擦角。从图中可以看出，同样孔隙比和同样的围压的试样，在不同的荷载条件下，平面应变试验试样的峰值摩擦角最大，直剪试验峰值摩擦角最小，三轴压缩试验居中。同样的荷载条件下，围压越大则峰值摩擦角越小，孔隙比越低峰值摩擦角越大。对临界摩擦角，仍然是平面应变试验试样的临界摩擦角最大，三轴压缩试验居中，直剪试验最小。但是，在相同的荷载条件下，围压和孔隙比对临界摩擦角的影响不大。这些结论与之前学者进行的理论研究、试验分析以及数值模拟的结果相一致。
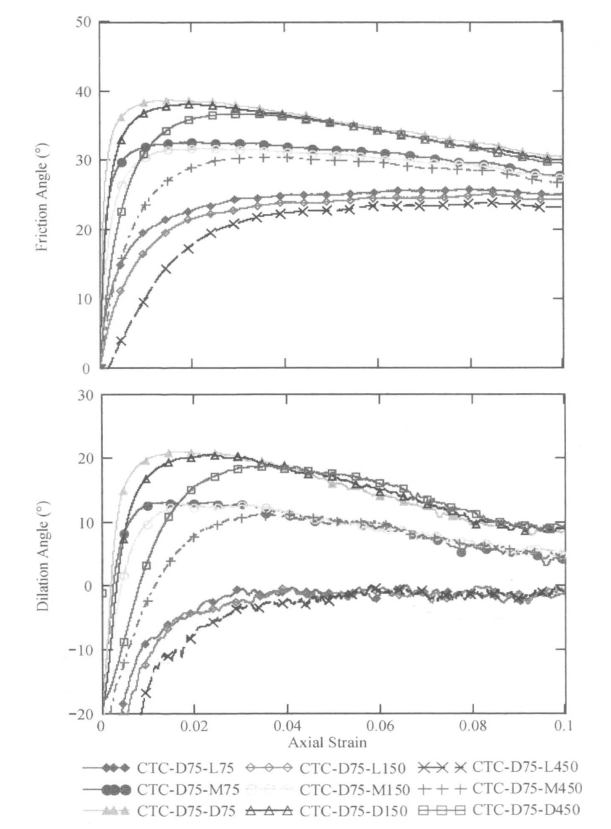
图4.6 三轴压缩试验摩擦角和膨胀角与轴应变的关系
图4.7 直剪试验摩擦角和膨胀角与水平应变的关系
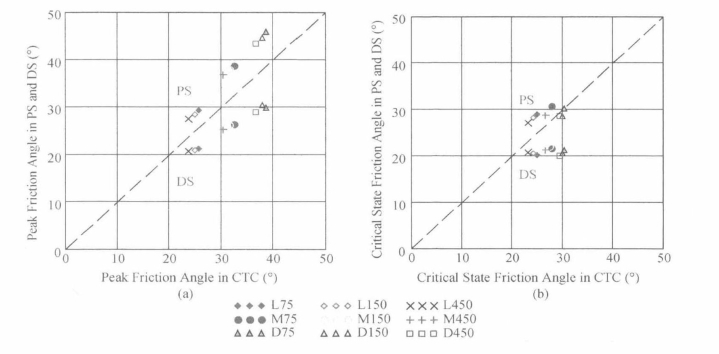
图4.8 平面应变、三轴压缩、直剪试验（a）峰值、（b）临界摩擦角的比较
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
