断层地质结构三维建模

断裂构造是地壳上发育最广泛、最常见的一种地质构造,它使岩体的连续性和完整性遭到破坏,并使断裂面两侧岩块沿破裂面发生位移。发生明显的相对位移或仅有微量位移的断裂构造,称为节理;发生较大和明显的相对位移,称为断层。在水利水电工程地质中,主要考虑以断层为主的断裂构造。

断层类对象主要包括断层、侵入体、深裂缝和层内错动带四类地质结构,下面将主要以断层为主来说明该类地质对象的几何建模理论与方法。

大量的研究表明,断层处理是三维地质建模的难点之一,目前仍处于探索阶段。断层建模的主要问题是连接剖面之间断层轨迹线的多解性以及缺乏对断层变形和对其进行三维外推的丰富信息。而且在水利水电工程地质构造复杂的区域,众多的断层互相交错发育,在地质岩体内形成了复杂的断层网络,因此,除了精确构造单个断层外,还要从整个断层网络系统出发,正确处理好多个断层相交的错动问题。然而目前的研究主要是针对单个断层或至多两个相交断层的构造建模,对于如何客观地重建一个复杂的断层网络,几乎未有涉及。本书将以众多交错断层发育的某工程地质区域为实例,为包含断层的复杂地质体建模提供完整的、切实可行的解决方案。

5.3.3.1　单个断层建模

对于单个孤立的断层,可以根据钻孔、平硐数据、解译形成的剖面信息以及区域地质调查获得的有关数据,首先利用NURBS算法形成两个主要的断层面,并经过边界约束和尖灭等条件处理,建立合理的断层面;然后利用这两个断层面相应的边界线构建四个边界面;最后在满足一定精度的要求下,通过几何图形的集合运算对这六个曲面进行缝合,围限而成一个完整的断层体。

然而,从地质观点来看,一个断层可看成一个与地层相交的实体,并且断层和地层之间的关系并不是对称的,其关系为:断层切割地层,地层有位于断层上的边界线,如图5.18所示,因此断层建模必须同时考虑地层的切割。从数学角度来看,一方面断层是几何上的不连续,另一方面断层可被当作是一种地层线性几何不连续两侧部分之间的超连接,因为在地层被断层切割之前,它是连续的,当模拟一个被错断的地层时,这种连续在断层两侧存储。实质上,模拟一个断层与一个地层相交错断的情况与两相交断层建模的原理是相同的,下面将进行详细研究。

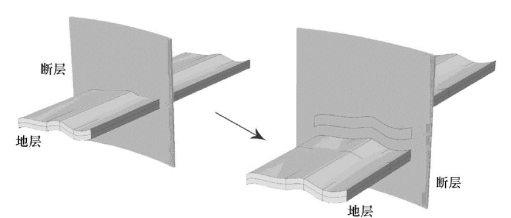
图5.18　地层沿断层错断滑动

5.3.3.2　两相交断层建模

在地质构造复杂的工程区域,若断层较为发育时,会出现断层两两相交错动的现象,如图5.19所示,这和断层将地层错断的情形类似。根据解译出来的断层产状和构造特征,可以推断先发育形成的断层F2[图5.19(a)]和F4[图5.19(b)]分别被后发育形成的断层F1[图5.19(a)]和F3错动[图5.19(b)]。

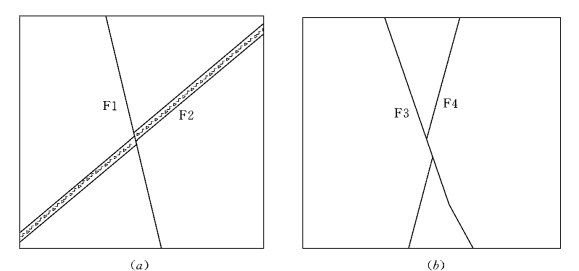
图5.19　不同错动下的两相交断层

(a)小错动位移;(b)大错动位移

对于两相交断层的构造建模,首先需要引入以下两个约束条件:

(1)边界约束(On Tsurf约束)。相应于主断层的上升盘与下降盘的被错断层边界任何时刻都应该位于该主断层上。

(2)矢量连接约束(Vec Link约束)。被错断层由错动引起的位移,可以通过在主断层的上升盘和下降盘之间设置位移向量来实现。

针对图5.19中的两种不同情况,可分别采用不同的方法进行构造建模。

(1)被错断断层的两部分之间位移较小。如图5.19(a)所示,F1错断F2,F1仍然是一个完整体,而F2被分成两个微小错距的不连续部分。首先对断层F1建模;然后对于断层F2,由于其两部分之间的相对位移很小,在精度允许情况下,可以把它们按照错动方式直接连接成一个整体,利用NURBS技术进行构建;最后利用F1通过布尔运算,切割错断F2,这样构造出的相交部分不仅能够满足精度要求,而且还同时满足了上述两个约束条件。

(2)被错动断层的两部分之间位移较大。如图5.19(b)所示,F3错动F4,F3是一个完整体,F4则被F3切割错断为相对位移较大的不连续的两部分。在这种情况下,若仍把F4连接为一个整体进行构建,则在转折处易产生较大的突变,断层体F4和F3在相交处难以精确吻合,误差较大。因此,考虑把位于F3上升盘和下降盘的F4不连续的两部分分别进行构造建模,这能够满足Vec Link约束;在构建过程中,调整F4两部分与F3相交处的边界,使其边界线均位于F3断层体上,以满足On Tsurf约束。这样就能够获得精度高且满足两个约束条件的断层模型。

5.3.3.3　复杂断层网络构造建模

对于断裂构造极其发育的工程区域,众多的断层相互交错形成复杂的断层网络。图5.20所示实例共包含7条存在相互关系的断层。该断层网络的建模相对更为复杂,主要思路是在两相交断层构造的基础上,根据断层网络中各个断层的产状、构造特征和错动关系分析出各自的历史形成,引入拓扑排序方法,对发育、构造形成的先后关系进行排序,然后依序针对具体情况采用不同的方法构造,实现复杂断层网络的三维建模。

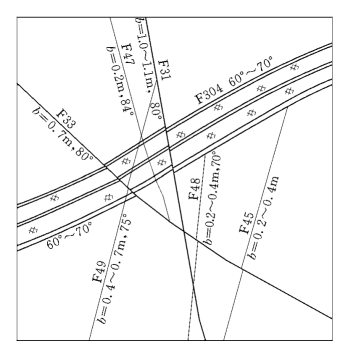
图5.20　复杂断层网络实例(高程135.0m)

(1)拓扑排序原理及算法实现。若集合X上的关系R是自反的、反对称的和传递的,则称R是集合X上的偏序。设R是集合X上的偏序,若对每个x、y∈X,必有x Ry或y Rx,则称R是集合X上的全序。由某个集合上的一个偏序得到该集合上的一个全序,这个操作称为拓扑排序。

拓扑排序是有向图的一种重要运算。一个偏序的有向图可用来表示一个流程图;用顶点表示活动,用有向边表示活动间优先关系的有向图称为活动节点(Activity on Vertex,AOV)网络。

设G=(V,E)为一个AOV网络,V是节点的非空有穷集合,E是边的集合。对于任意的v∈V,称{u|u∈V∩〈u,v〉∈E∩u≠v}为v的前驱元集,即所有先于节点v且与v之间存在有向路径的节点均是v的前驱节点;当节点u、v是一条边〈u,v〉上的两个端点时,称v为u的直接后继节点。图5.21给出了一个AOV网络示意图,节点v1的前驱元集为{v2,v3,v4,v5,v6},其中v2、v3、v4是v1的直接后继节点。显然,AOV网络中不能出现有向环,否则对应的活动便无法进行。

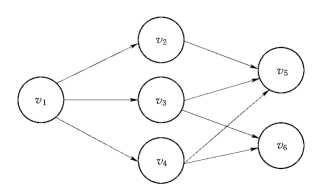
图5.21　AOV网络示意图

V中节点的线性序列(vi1,vi2,…,vin)称为一个拓扑序列。任何有向无环图的节点都可以安排在一个拓扑序列中。若在G中从节点vi到节点vj有一条路径,则在序列中,vi必在vj之前。拓扑排序方法过程描述如下:(www.xing528.com)

1)AOV网络中各边的网络节点按先后顺序构成的序偶〈vi,vj〉依次输入,形成n个链表(n为顶点的个数)。

2)在AOV网络中任意挑选没有前驱的节点。

3)输出该节点,并将与该节点相连的所有边删除。

4)重复步骤2)和步骤3),直到全部节点都输出为止,拓扑序列形成。

由于整个过程中经常会有数个无前驱的节点供选择,故AOV网络的拓扑序列并不唯一,选择不同的节点便会产生不同的排序结果。

拓扑排序方法主要应用于工程施工组织、产品生产流程设计等方面。引入该方法的思想,考虑历史活动形成过程的复杂断层网络,可以用AOV网络来表示,并进行拓扑排序,确定各个断层的构造顺序序列,有利于断层网络按照准确的历史次序进行建模。

拓扑排序可以在AOV网络的不同存储表示上实现,如相邻矩阵表示和邻接表法。相邻矩阵存储表示所进行的拓扑排序,程序简单,但处理的效率低;而采用邻接表作为AOV网络的存储结构,可显著提高拓扑排序的效率。对于包含n个节点的AOV网络,该方法在节点表里每个节点结构中加一个in字段,内容是该节点的入度;这样只需检查n个元素的数组就能找到入度为0的节点,进一步可用入度为0的节点字段构造一个链接方式存储的栈,把所有入度为0的节点都推入栈中。排序开始时,从栈顶取出一个节点,检查它的出边表。对每条出边的终点,把它的节点表里对应的in字段值减1。若某个节点的入度减为0,就把它推入栈里去,直至栈为空,排序结束。

邻接表数据存储结构相关的变量如下:

(2)断层AOV网络的建立与拓扑排序。根据上述原理,可将复杂断层网络定义为AOV网络模型,AOV模型的拓扑序列即为各个断层的构造顺序序列。该模型可定义为:

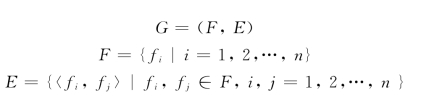
这里F表示断层网络中断层体的集合,用AOV模型的节点表示;E表示F中元素有序对的集合,即AOV模型的边,它代表两相交断层fi和fj的构造交错关系。〈fi,fj〉表示该边的起点(断层fi)历史形成早于该边的终点(断层fj),且断层fj切割错断断层fi,或者断层fj发育空间展布终止于断层fi。

在AOV模型中,如果一个节点的入度为0,则意味着该节点所代表的断层形成发育较早,但并不能说明其构造最早,还需与其他入度为0的断层进行客观的对比分析,以确定其先后关系。最后得到的有向序列f1→f2→…→fn,即表示由n个断层构成的断层网络中各个断层体的先后构造顺序,这样使得该断层网络的几何建模能够客观真实地反映由断层的历史形成先后关系和交错移动的空间拓扑关系。

以图5.20所示的由7条断层组成的断层网络为例,根据断层的产状和构造特征分析出各自的历史成因,确定两两形成的先后及错动关系,则可得到以下多组有序对:

(F304,F49),(F304,F31),(F304,F33),(F304,F47),(F304,F48),(F304,F45),(F49,F33),(F49,F47),(F31,F33),(F33,F47),(F48,F31),(F48,F33),(F45,F33)。

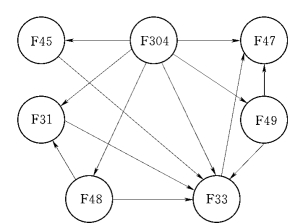
图5.22　复杂断层构造的AOV网络模型

如此,建立相应的AOV网络模型,如图5.22所示。

根据有序对关系,对上述AOV模型进行邻接表的存储,其存储结果如图5.23所示,以便于运用拓扑排序算法进行排序。

建立了断层网络的AOV模型,并以邻接表存储表示后,就可以利用拓扑排序算法得到AOV模型的拓扑序列,即断层网络中断层体的构造顺序,所得结果如下:

F304→F45→F48→F31→F49→F33→F47

在统一空间坐标系统下,按照这个先后顺序依次构造各个断层体,并根据5.3.3.2节两相交断层的处理方法,构建完整的断层网络模型,如图5.24所示。从图5.24可以看出,由于面向历史过程充分考虑了断层的构造形成和相互交错情况,所构建的三维模型不仅精确地揭示了该工程区域内断层在地质岩体中的空间展布,而且真实客观地再现了断层历史形成条件下的空间关系。

图5.23　断层AOV网络模型的邻接表存储表示

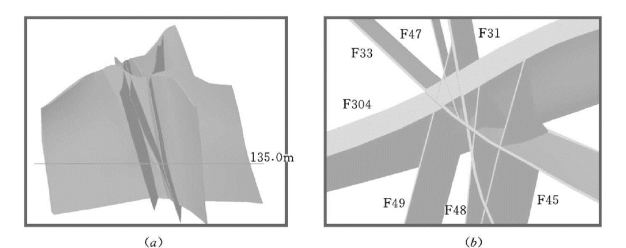
图5.24　复杂断层网络三维构造模型

(a)整体模型;(b)高程135.0m平切图