三维几何对象的任意布尔算法在水利水电工程分析中的应用

由于三维地质模型是采用NURBS技术来实现地质体重构的,因此面与体、体与体两者之间的布尔切割运算的基本原理是相同的,其算法过程主要包括:检查两个对象是否相交、求两个对象各表面之间的交线、判定分类两个对象的表面、建立新的数据结构四个步骤。不失一般性,下面重点讨论体与体之间的集合(并、差、交)运算。假设A、B两个岩层实体,布尔模型C=A＜OP＞B,其中＜OP＞代表∪(并)、-(差)、∩(交)等布尔算子,按照上述四个步骤详细介绍三维几何对象的任意布尔切割算法原理。

(1)检查是否相交。这样能够简单地判定两个物体或一表面同另一物体许多不相交的情况,从而避免许多不必要的复杂求交计算。检查又可以分为两步:

第一步比较两个物体各自的包围盒(最大、最小方盒或包围球面)是否相交,最大、最小方盒计算简单,设物体A、B的最大、最小方盒分别为(xAmin,xAmax,yAmin,yAmax,zAmin,zAmax)和(xBmin,xBmax,yBmin,yBmax,zBmin,zBmax),当满足下列六个条件之一时,A、B不相交。

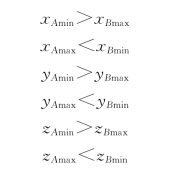
若上述条件均不满足,则进行第二步,分别将A、B上的每一个面同另一个物体进行相交判断,即将该表面的包围盒同另一物体的包围盒比较,在无法分离两包围盒时才将该表面同另一物体的所有表面一一求交计算。

(2)计算交线。计算两物体表面之间的交线是整个运算的核心,直接影响到操作的效率和速度。计算交线的方法有解析法和离散法。解析法虽然求解精度高、稳定可靠,但其交线方程的建立依赖于两相交曲面的解析性质,而复杂地质曲面的交线往往很难也无必要建立解析式精确地加以描述,因此选择采用离散法求交。首先将相交表面分别用一块块小平面去逼近,然后用这些小块平面之间的交线来近似表示两表面之间的交线。用平面片逼近曲面有均匀网格逼近和适应分割逼近两种方法,本书采用算法简单的均匀网格逼近,即沿曲面的u、v两参数方向均匀取点。如图5.13所示,每一参数方向的采样步长决定于曲面沿该方向的曲率变化情况,采样点在曲面上组成均匀矩形网格,其数据结构可取数组形式,然后用相邻网格点组成的四边形(近似平面)去逼近整个曲面。离散求交法计算简便,求交程序与表面的解析性质无关,程序相对统一;缺点是解的精度低,存在逼近误差,有时出现病态情形(如求得的交线不连续),因此可以适当考虑结合解析方法求取交线上的若干关键点,并强制交线通过这些点。

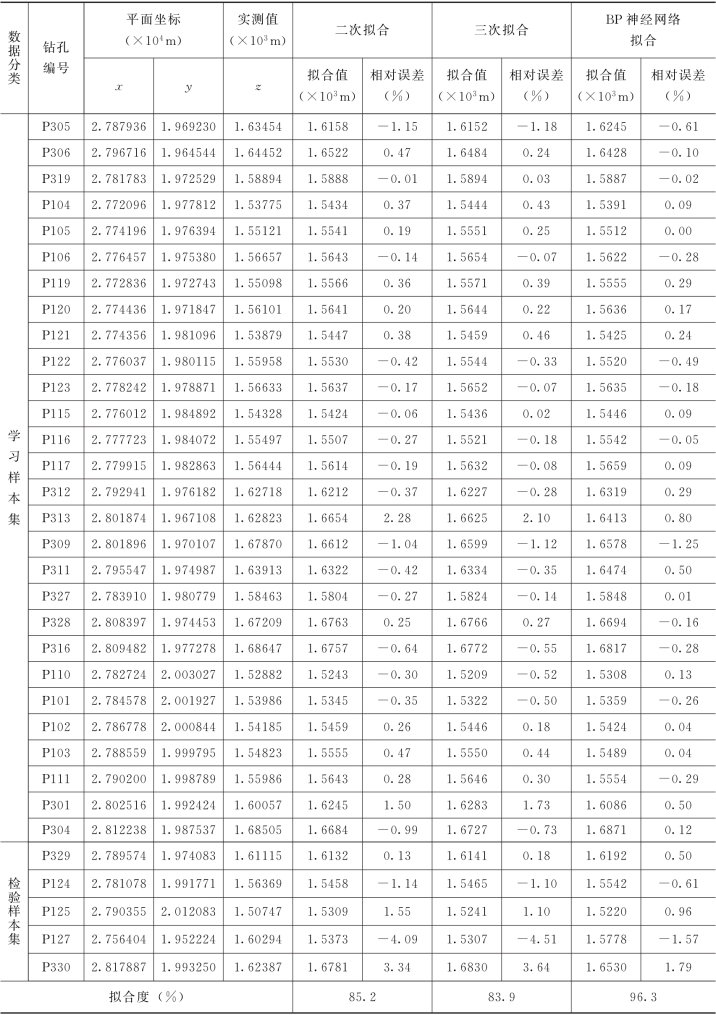
表5.1　岩层界面钻孔数据分析对比

(3)表面的判定分类。A、B两物体的交线将它们的表面分割成两部分,一部分在拼合体表面上形成新的边界,另一部分位于拼合体内或体外,应在集合运算最后删除。在边界表示法中,物体的表面均有确定的外法向,因此可以把A上的所有表面根据对B的关系分为四个子集合:AinB、AoutB、ABshared、ABanti-shared。其中AinB和AoutB分别表示A所有表面位于B体内和体外的部分,ABshared和ABanti-shared分别表示A表面和B表面重合的部分中其外法向与B表面法向相一致的部分和相反的部分。同样地,用BinA、BoutA、BAshared和BAanti-shared表示B上所有表面对A的分类,且有ABshared=BAshared,ABanti-shared=BAanti-shared。根据集合运算性质,则有(www.xing528.com)

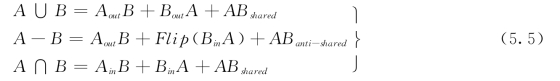
式(5.5)中函数Flip(f)表示对表面f的外法向取反。

(4)删去与结果无关的边界,建立新的数据结构。在求交过程中,在相交表面上会不断建立新的拼合体的表面边界,但此时还不能删去相交表面的原有边界,因为这些表面还可能与相交物体上其他表面相交,所以必须在求交过程中始终保持表面原有的边界信息不受破坏。只有在所有的求交计算结束后,各相交表面的原有边界才可以删去,同时某些位于拼合体外或体内的不相交表面也应该删去,最后根据新的数据结构获得所期望的新的物体。

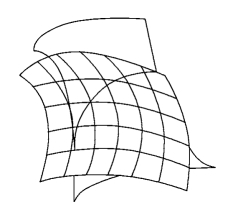
图5.13　均匀网格逼近曲面图

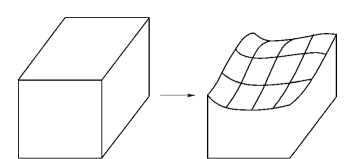
图5.14　物体表面的局部运算

上述算法中,若A、B分别由m、n个面组成,则其求交运算量为O(mn),效率较低。因此在一些实际情况中,只需对现有物体的形状作局部修正,为了减少运算量,可以引入局部运算。局部运算仅涉及对物体的几何信息或拓扑结构做某些局部的修改,比整体意义下的物体间集合运算效率高得多。如图5.14所示,将长方体的某一表面改变成曲面,只需在边界表示中改变表面的几何定义,并用曲面与原表面相邻面的交线作为新的表面边界即可。