地质趋势面分析技术在水利水电工程中分析理论实践中的应用

5.2.4.1　地质趋势面分析概述

虽然三维地质模型的实现主要依靠的是通过钻孔、平硐等勘探资料解译分析所得到的各种剖面图,但直接根据钻孔、平硐资料进行地质趋势面分析是对地质模型重构进行补充和验证修改的重要一环。

图5.10　地质结构单元实体模型

传统的地质趋势面分析是指用平面或曲面(包括n维空间的超曲面)对地质空间观测点的值进行拟合的一种多元回归统计分析方法。它将空间分布的地质特征,如地层厚度变化、构造层位顶面或底面的标高变化等地质变量,用数学方法区分为趋势部分和剩余部分。而地质变量的空间分布可表示为趋势面和剩余面结合形成的曲面,其中趋势面对应于一个确定函数,剩余面对应于一个随机函数。因此,地质趋势面分析的实质就是,用一定的函数对地质体某种特征的空间形态进行分析,用该函数所代表的曲面来拟合该地质特征的空间分布形态的趋势变化,将实测值中的趋势部分和剩余部分分离开来,从而发现其区域性变化规律和局部异常。

常用的趋势面分析方法主要有多项式趋势面和二维傅立叶趋势面两种,在地质构造的研究中,通常运用多项式趋势面进行拟合分析。多项式趋势面由幂级数组成,其优点是系数计算比较容易,且根据经验,很多地质变量(如地层层位)的高度、地下水位的高度及地层厚度等用较低次的多项式趋势面就能拟合得较好。假设所研究的某一地质区域内有n个钻孔观测点,在某一地层界面上第i个钻孔的地理坐标为(xi,yi,zi),其中以x、y为自变量,z为因变量,则一般二元p次多项式趋势面的数学模型为:

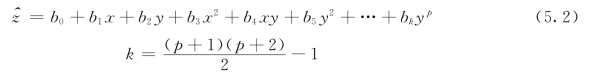
式中:p为多项式的次数;k为p次多项式的项数(不含常数项b0)。

根据最小二乘法原理可以确定系数b0、b1、b2、…、bk,并需对所求得的系数进行假设检验,是否满足期望要求。图5.11为两个自变量时一次、二次和三次多项式趋势面示意图。

图5.11　两个自变量的一、二、三次多项式趋势面示意图

值得注意的是,使用多项式趋势面并不能认为地质过程就是某个多项式函数的变化过程,因为地质对象有着很复杂的变化过程,形成具有复杂形态的曲面,多项式趋势面只是用来拟合这个复杂的曲面,并不能完全真实地反映实际的地质形态变化过程。

5.2.4.2　地质趋势面分析改进

对于上述拟合地质结构面的多项式趋势面分析,在拟合曲面和所分析的资料之间,不一定有内在的联系,甚至不同的函数可以产生几乎相同效果的拟合,这样对于复杂多变的地质实体,模拟可能出现较大的偏差。因此,考虑到一个复杂工程的地质系统,其最本质的属性包括非平衡性、非线性、多尺度性、突变性、自组织性、自相似性和随机性等,人工神经网络(Artificial Neural Networks,ANN)在这方面具有很大的优势,可以用来进行地质趋势面分析。由神经网络自动构建具有非线性映射关系的地质趋势面函数,将可以获得更接近实际的地质拟合曲面。

人工神经网络是由大量类似于神经元的简单处理单元相互联系而成的复杂网络巨系统。根据地质趋势面分析应用的实际问题,构造如图5.12所示的双输入、单输出地质趋势面的神经网络模型。图5.12中,xp(p=1,2)表示输入的大地坐标,z表示输出的地质构造变量值,如层面高程、岩层厚度、岩体力学参数等,它们之间关系表达如下:

式中:w1(k)为第k个隐含元到输出单元之间的权重;w2(p,k)为第p个输入元到第k个隐含元之间的权重;hk为第k个隐含元的输出值;θ1为输出元的阈值;θ2(k)为第k个隐含元的阈值;Sk为第k个隐含元的状态值。

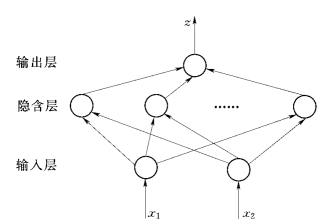
图5.12　地质趋势面分析的ANN模型

利用BP算法来训练和确定该ANN模型的结构及其参数。BP算法是一种求前向式多层网络的迭代梯度算法。标准BP算法有许多缺陷,如收敛速度慢、局部极值、难以确定隐含层和隐节点的个数,在实际应用中很难实现。实践表明,在MATLAB环境下开发的神经网络工具箱中采用改进的BP算法可以得到很好的实现,基本步骤为:(www.xing528.com)

(1)模型的初始化。在设计BP网络时,只要已知输入变量集合X={xp}、各层的神经元个数和传递作用函数f,就可以利用函数initff(X,k,f1,1,f2),对BP网络进行初始化,获得模型的初始权重和阈值,函数中f1、f2分别为隐含层、输出层所选定的传递作用函数。

(2)模型的训练学习。选择更为有效的Levenberg-Marquardt优化算法对传统算法进行改进,能使学习时间更短、精度更高,该算法的权值调整率选为

式中:J为误差对权值微分的Jacobian矩阵;I为单位矩阵;E为误差向量;μ为一个标量,当μ很大时,式(5.3)接近于梯度法,当μ很小时,式(5.3)变成了Gauss-Newton法,这里μ是可以自适应调整的。

该算法对应的训练函数为trainlm(w1,θ1,f1,w2,θ2,f2,X,Z,tp),该函数中Z为学习样本中的输出值集合,tp为训练参数,主要包括最大训练次数、误差指标等。该函数通过迭代计算可获得满足误差目标的最优权重和阈值。

(3)模型的输出。根据学习所得到的最优权值和阈值,利用函数simuff(X,w1,θ1,f1,w2,θ2,f2)输出的结果来检验或作出预测。

通过上述训练确定的ANN模型即可用于地质构造趋势分析的拟合与外推插值。

5.2.4.3　实例对比研究

以锦屏一级水电站工程中地质岩层上界面的实际钻孔数据为例,根据与该地层面相交的钻孔平面坐标(x,y)对钻孔在该面上的相交高程z值进行趋势面分析。

趋势面分析是对三维坐标点的数据分析,数据量较大,因此首先要进行数据筛选和标准化预处理:即先从所有的实际钻孔中筛选出与该地层界面相交的钻孔坐标,整理所得的共33个数据样本;由于x、y、z三个坐标的实际数值都很大,不利于进行拟合,因此分别将其进行极差正规化处理,这是一种处理地质变量的常用标准化方法,具体变换公式为:

式中:x′i为变换后的数据;xi为变换前的数据;n为取样钻孔总数。

取前28个数据样本作为学习样本集,后5个作为检验样本集,分别使用二次多项式、三次多项式和BP神经网络拟合后,所得数据对比如表5.1所示。其中拟合值是根据已知钻孔坐标构造函数后计算得出的,相对误差则是拟合值相对实际z值的误差。拟合度按下式计算:

计算所得的二次和三次拟合多项式分别为:

含有一个隐含层神经元个数为5的三层BP神经网络在Matlab上仅经过15次学习,即达到误差要求0.001,所确定的最优权值(w1,w2)和阈值(b1,b2)矩阵如下:

对比表5.1的结果,可以看出二次和三次拟合多项式的效果相差不多,总体上二次甚至比三次更好;BP神经网络在学习拟合和外推插值效果两方面都要好于多项式的结果,拟合度高达96.3%,说明神经网络由于其自身的特性,在处理地质趋势面分析方面有其优越性。