地质结构单元实体模型NURBS构造技术

5.2.3.1　地质结构面的NURBS构造

地质结构面是地质体中具有一定方位、两向延伸的地质界面的统称,包括物质分异面(如层面、片理面、软弱夹层、侵入体接触面等)和不连续面(如断层、节理、风化与卸荷裂隙等)。而相应的地质结构体受结构面发育、排列与组合的制约,就岩体结构来说,结构面是主导的,结构体则是由结构面围限而成;岩体结构即是由结构面和结构体共同构成的结构形态。因此,地质结构面的构造实现是各类地质结构体建模的基础。本章主要阐述一般地质结构面的NURBS构造技术。

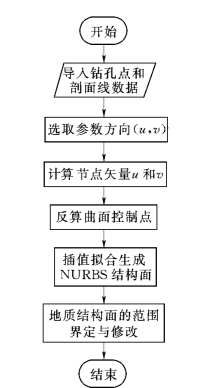
图5.8　地质曲面NURBS实现流程图

第四章已对NURBS技术基本原理作了较为详细的介绍,根据其理论方程,NURBS曲面主要是通过控制点计算实现的,因此根据已知的数据信息拟合NURBS曲面的方法有两种:①若已知数据信息为控制多边形的顶点,则称为正算法,这是数学上的计算几何常采用的;②若已知数据信息为曲线上的型值点,则要先求出控制多边形的顶点,再拟合NURBS曲面,即反算法。在实际工程地质中,已知的钻孔数据点和剖面线信息都是地质结构面上实际的数据点阵,不能直接构造NURBS曲面,因此应该采用反算法。反算法可描述为:

(1)根据数据点阵的空间分布,分别选取u、v参数为截面和纵向参数方向。

(2)对所给曲面数据点实行规范修正弦长或均匀参数化(视具体情况定),确定两个参数方向的节点矢量。

(3)第一次反算,将u参数方向上的数据点依次按曲线反算出一系列点。

(4)第二次反算,将第一次反算得到的点在v向节点矢量上应用曲线反算,所得到的即为曲面的控制点。

以某一地质区域中的单个简单地层界面(忽略断层等其他构造的影响)NURBS拟合构造为例,实现流程如图5.8所示,数学计算过程已封装在底层。基本步骤如下:

(1)根据研究区域地质横剖面图、平切图以及该结构面上的钻孔点数据,得到该层面上u、v方向的曲线矢量。(www.xing528.com)

(2)利用反算法求出各曲线矢量上的控制点,如图5.9(a)所示。

(3)设置所有控制点的权值均为1,对所有控制点插值拟合,构造出该界面的NURBS曲面,其u、v向的网格点阵可任意交互给定,这里选为70×100;该曲面可通过重复调整任意控制点权重(0.1～10范围内)来进行修改。

(4)对所形成的曲面进行边界范围界定,并作出相应的修剪,最后生成的NURBS网格曲面如图5.9(b)所示。

5.2.3.2　地质结构单元实体模型

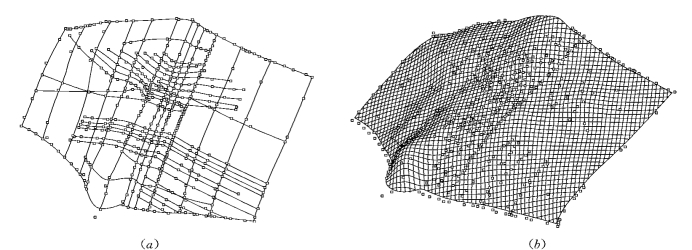
图5.9　简单地层面的NURBS拟合

传统的地质单元划分通常将本身是一个整体的地质结构体剖分为诸多定义的最小单元体的集合。一般情况下,基于此类地质单元的三维实体重构模型虽然能够满足精度要求,但往往不可避免地增加空间或时间的开销,对于水利水电工程区域大规模数据整体建模应用,必然影响地质分析速度,不能实时响应用户操作,无法得到满意的效果。因此,基于地质结构面的NURBS实现,遵循客观地质规律,以各类单个地质结构整体作为相应的地质单元,笔者提出了通用的地质结构单元实体重构模型。

上述地质结构面实际上是由各层面上的离散点和线数据构建而成的,而地质结构体又是基于不同结构面组成的,假设重构模型空间研究区域为Ω,则基于地质结构单元的整体地质模型数学定义如下:

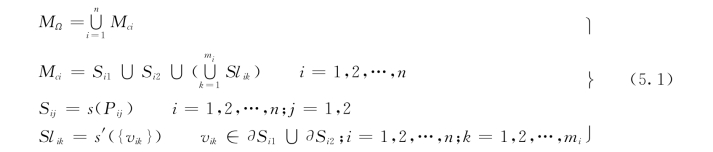
式中:MΩ为研究区域Ω的整体地质模型;n为Ω中包含的地质结构单元实体总数;Mci为Ω中的第i个地质结构单元实体模型;Si1、Si2分别为构成Mci的上、下(或左、右)主结构面,由其层面上的点集Pi1、Pi2通过NURBS技术拟合构造而成;∂Sij为结构曲面Sij上所有边界顶点的集合;Slik为连接Si1、Si2,形成闭合实体Mci的第k个边界面,是由边界顶点集合{vik}形成的简单NURBS曲面;mi为第i个单元中连接边界面的数目。

图5.10给出了一个简单地质结构单元的实体模型。由空间分割原理可知,任何具有复杂几何形态的对象都可以分解为有限个简单单元形状,通过式(5.1)重构地质模型,可以完整、快速、客观地描述复杂地质体的空间几何形态。