水利水电工程地质BRep结构分析实践

在实体建模中,BRep结构通过其边界面来定义实体,为对象提供有效的体描述。在一个边界表示结构中,其边界可以是任意类型的有边界、可定向的自由曲面,在数据结构中,构成地质实体的边界面主要为NURBS曲面,图3.5给出了一个BRep实体的例子。

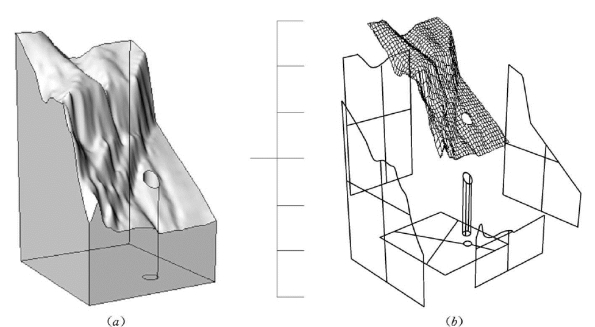
图3.5　BRep实体结构示意图

(a)BRep实体;(b)分解边界面

BRep结构描述物体的信息包括拓扑信息与几何信息两个方面。物体的拓扑信息指物体上所有的顶点、棱边、表面间是如何连接的,拓扑关系形成物体边界表示的框架;几何信息给出了构成物体所有几何元素的定义数据,描述物体的大小、尺寸、位置、形状等。拓扑信息与几何信息分开表示有较多优点:①便于具体查询物体中各元素,获取它们的有关信息;②对物体的各种局部操作容易,而不必修改物体的整体数据结构;③对于具有相同拓扑结构而只是大小、尺寸不同的一类物体可以用统一的数据结构表示;④便于在数据结构上附加各种非几何信息,如某地质曲面的产状属性。(www.xing528.com)

边界表示法的数据结构有翼边结构和半边结构,翼边结构提出较早,存在一些缺陷,于是人们在此基础上提出了更为完善的半边结构。基于BRep数据结构,可以直接使用顶点(Vertex)、棱边(Edge)、表面(Face)等基本元素通过欧拉运算来构造复杂三维对象实体。顶点、棱边和表面之间必须满足一定的关系,即几何一致性和拓扑一致性。几何一致性应由用户输入相应几何信息时予以保证,同时系统提供检查功能。而它们所要满足的拓扑关系则可用下列扩展欧拉公式表示:

式中:v、e、f分别为物体上的顶点数、棱边数及表面数;r、h、s分别为物体表面边界的内环数、不相连接的物体个数及物体上的通孔数目。

近十多年来,利用BRep结构进行地质实体建模得到了国内外学者的广泛关注,并提出了各种不同的拓扑模型来描述复杂的地质结构体。Lamboglia(1994)提出了非流形BRep结构进行地质体建模;Halbwachs等人(1996)利用三维广义图(3-G-Maps)的边界表示数据结构,实现了断层网络结构的拓扑和几何描述;Euler等人(1998,1999)在一个新的建模工具中,基于BRep结构加入约束条件,能够建立、编辑并快速更新封闭的三维地质模型;Caumon等人(2003)成功地对三角化的非流形BRep地质结构进行了局部约束修改更新;周爱华(2003)提出了CAD边界表示法来构造三维地质体信息模型,在AutoCAD环境下利用BRep实现了地质体的三维可视化;Caumon等人(2004)在传统BRep有效性条件基础上提出了两条地质结构有效性准则,实现了封闭地质模型的交互建立和编辑。