TIN模型的应用-水利水电工程地质三维建模与分析理论及实践

在三维地质建模与分析体系中,TIN主要是用来实现工程区域复杂的、不规则的地形形态由等高线到NURBS数字地形模型(Digital Terrain Model,DTM)的转换过程。由于实测的原始等高线数据往往不能很好地描述悬崖、沟壑,出现不连续的现象,不能直接用来建立NURBS DTM,而TIN模型能够很好地表示这些特殊复杂地形的造型,因此考虑基于TIN模型对其进行处理。

TIN模型根据区域内有限个点集将区域划分为相连的三角面网络,区域中的任意点落在三角面的顶点、边上或三角形内。若点不在顶点上,该点的高程值通常通过线性插值得到(在边上用边的两个顶点的高程,在三角形内则用三个顶点的高程),所以TIN是一个三维空间的分段线性模型,在整个区域内连续但不可微。对于不规则分布的高程点,可以形式化地描述为平面的无序点集P,P中每个点对应其高程值。将该点集转化为TIN,最常用也最出色的方法是Delaunay三角剖分方法。

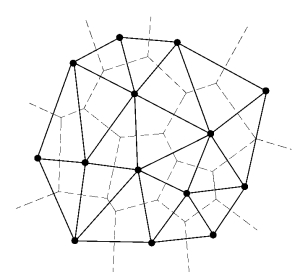
图3.4　Delaunay三角网示意图

Delaunay三角网由对应Voronoi多边形共边的点连接而成。Voronoi图又称为泰森多边形或Dirichlet图,由一组由连接两邻点直线的垂直平分线组成的连续多边形组成。Delaunay三角形由三个相邻点连接而成,这三个相邻点对应的Voronoi多边形有一个公共的顶点,此顶点同时也是Delaunay三角形外接圆的圆心。图3.4描述了欧几里德平面上14个点的Delaunay三角形和Voronoi图的对偶,其中实线为Delaunay三角形,虚线为Voronoi图。

对于给定的初始点集P,Delaunay三角网剖分具有以下特征:①Delaunay三角网是唯一的;②三角网的外边界构成了点集P的凸多边形外壳;③每一三角形的外接圆内部不包含其他的点(空圆特性);④任意两个相邻三角形形成的凸四边形对角线如果可以互换的话,那么两个三角形6个内角中最小的角度不会变大,Delaunay三角形网总是具有最优的形状特征。(www.xing528.com)

构造Delaunay三角形网方法有分而治之算法、逐点插入算法和三角网生长算法等,其中通用的是逐点插入算法。结合地形等高线数据的特征,为克服基于散点构网算法的缺点,提高算法效率,可对网格中三角形的空圆特性稍加放松,采用基于边的构网方法,其改进的逐点插入算法实现过程如下:

(1)根据已有的地形等高线和特征线,形成控制边链表。

(2)以控制边链表中某一线段为基边,从点集(通过等高线离散得到)中找出同该基边两端点距离和最小的点,以该点为顶点,以该基边为边,向外扩展一个三角形(仅满足空椭圆特性),并放入三角形链表。

(3)按照步骤(2),对控制边链表所有的线段进行循环,分别向外扩展。

(4)依次将新形成的三角形边作为基边,形成新的控制边链表,按照步骤(2),对控制边链表所有的线段进行循环,再次向外扩展,直到所有三角形不能再向外扩展为止。