律書第三
（律數）九九八十一以爲宫。三分去一，五十四以爲徵。三分益一，七十二以爲商。三分去一，四十八以爲羽。三分益一，六十四以爲角。
黄鐘長八寸七分一，宫。大吕長七寸五分三分二。太簇長七寸十分二，角。夾鐘長六寸七分三分一。姑洗長六寸十分四，羽。仲吕長五寸九分三分二，徵。蕤賓長五寸六分三分二。林鐘長五寸十分四，角。夷則長五寸三分二，商。南吕長四寸十分八，徵。無射長四寸四分三分二。應鐘長四寸二分三分二，羽。（4/1249/6-13）
《夢溪筆談》謂餘分下分數目，凡“七”字皆當作“十”，字誤屈其中畫耳。黄鐘八寸十分一，太簇七寸十分二，姑洗六寸十分四，林鐘五寸十分四，南吕四寸十分八。宋蔡元定《律吕新書》因之，皆改“七分”爲“十分”。然《索隱》已先言“七分”爲誤矣。又《新書》改大吕爲七寸五分三分二，夾鐘爲六寸七分三分一，蕤賓爲五寸六分三分二，夷則爲五寸三分二（“五寸”下當作兩空圍，“三分二”是小分也）。又云：“黄鐘下有宫，太簇下有商（蔡據宋本作“商”，今本皆作“角”字）。姑洗下有羽，林鐘下有角，南吕下有徵。《晉志》論《律書》五音相生，而以宫生角，角生商，商生徵，徵生羽，羽生宫。求其理用罔見通途者是也。仲吕下有徵，夷則下有商，應鐘下有羽，三者未詳，疑後人誤增。”蔡氏之説如此（《史詮》《正譌》亦以“徵商羽”三字疑衍，從蔡氏也）。而《史詮》曰：“太簇‘角’當作‘商’，姑洗‘羽’當作‘角’，林鐘‘角’當作‘徵’，南吕‘徵’當作‘羽’，俱後人傳寫之誤。”要之，史公所記分寸之數，配合之數，與《管子》、《吕覽》、《淮南》及漢、晉以來諸志皆不同，而後人譏之者甚衆，展轉糾繣，莫適是非。蒙不知律，未敢妄談，姑取先儒所改正者著之，以俟專家質焉。昔高誘注《淮南》不解鐘律上下相生之法，置而不説，余竊同之矣。（2/762/12—763/6）
按：律吕是古樂理的基石，而律數又爲樂理之核心，但時至今日，學界對律數的理解仍存有不少疑問，今一一析而辨之。
今本《史記·律書》“律數”一節，具體律數的數字分爲前後兩組。第一組：八十一、五十四、七十二、四十八、六十四。第二組：八寸七分一、七寸五分三分二、七寸十分二、六寸七分三分一、六寸十分四、五寸九分三分二、五寸六分三分二、五寸十分四、五寸三分二、四寸十分八、四寸四分三分二、四寸二分三分二。
梁氏所見《史》本《律書》“律數”第二組數字，其文曰：“黄鐘長八寸七分一，宫。大吕長七寸五分三分一。太簇長七寸七分二，角。夾鐘長六寸一分三分一。姑洗長六寸七分四，羽。仲吕長五寸九分三分二，徵。蕤賓長五寸六分三分一。林鐘長五寸七分四，角。夷則長五寸四分三分二，商。南吕長四寸七分八，徵。無射長四寸四分三分二。應鐘長四寸二分三分二，羽。”史文與今本略異，故梁氏始有上述之論。
《史記·律書》原爲《兵書》，其“序”亦爲原《兵書》之遺文，“序”文之外言律内容多爲後人割裂、拼凑原《律曆書》而成，經後人移動，已非太史公書原貌，[1]加以《史記》版本繁夥，異文便大量地産生，使得《律書》文字多有錯譌。“律數”一節，各具體律數的數字及十二律與五聲之關係等，都在一定程度上出現了譌誤，且學界對於這兩組律數的性質和來源，仍存有不少疑問，至今都没有形成一個有説服力、統一而清晰的認識。[2]
太簇長“七寸十分二”、姑洗長“六寸十分四”、林鐘長“五寸十分四”、南吕長“四寸十分八”，此“十分”原皆作“七分”。今本《史》文已全部校改爲“十分”，甚是。然而，黄鐘長“八寸七分一”却不作校改。司馬貞、沈括、蔡元定、錢塘、王元啓、瀧川資言、丘瓊蓀等歷代學者皆認爲黄鐘之長當校作“八寸十分一”。
《吕覽》《淮南》《漢書》等古籍關於黄鐘長度的記載皆爲“九寸”，甚至《史記》他篇的記載亦同，但《律書》此處的記載却爲“八寸七分一”，顯然兩數不等。我們怎麽解釋這種矛盾現象？兩組律數之間是什麽關係？各是什麽性質？來源爲何？歷代研究者形成以司馬貞、朱熹、蔡元定、王元啓、瀧川資言、丘瓊蓀等爲代表的“九進制”、“十進制”合用説和以沈括、錢塘、黄大同等爲代表的“實積”説。
司馬貞《索隱》將黄鐘長校作“八寸十分一”，曰：“上文云‘律九九八十一以爲宫’，故云長八寸十分一，宫。而云黄鐘長九寸者，九分之寸也。劉歆、鄭玄等皆以爲長九寸即十分之寸，不依此法也。云宫者，黄鐘爲律之首，宫爲五音之長，十一月以黄鐘爲宫，則聲得其正。舊本多作‘七分’，蓋誤也。”[3]
蔡元定《律吕新書》引《律書》第二組律數，曰：“《律書》此章所記分、寸之法，與他記不同。以難曉，故多誤。蓋取黄鐘之律九寸，一寸九分，凡八十一分。而又以十約之爲寸，故云八寸十分一。本作‘七分一’者，誤也。……大要《律書》用相生分數，相生之法，以黄鐘爲八十一分。今以十爲寸法，故八寸一分。《漢前後志》及諸家用審度分數，審度之法，以黄鐘之長爲九十分，亦以十爲寸法，故有九十分。法雖不同，其長短則一。”[4]朱熹在蔡氏書之序言中對此評論道：“其言雖多出於近世之所未講，而實無一字不本於古人已試之成法。蓋若黄鐘圍徑之數，則漢斛之積分可考；寸以九分爲法，則《淮南》、太史、小司馬之説可推。”[5]
王元啓《史記三書正譌》“九九八十一以爲宫”條，嘗曰：“前云得九寸爲黄鐘，是謂十分之寸。此復用九分之寸者，取其布算爲便，文異而理則同。”[6]其書“黄鐘長八寸十分一，宫”條引述《索隱》之説，曰：“今本泰簇、姑洗、林鐘、南吕四律猶作‘七分’，蓋由校讎之不審也。今依《索隱》注悉爲改正。”[7]
瀧川資言《史記會注考證》將黄鐘長校作“八寸十分一”，曰：“《史》此文曰‘黄鐘長八寸十分一’，下文及《淮南子》曰‘九寸’，蓋一以漢尺言，一以古尺言，其餘概皆吻合。”[8]
丘瓊蓀《歷代樂志律志校釋》將《律書》黄鐘長校作“八寸十分一”，説：“比率與長度，不能混而爲一，雖長度亦基於比率，有比率即可以定長度，然長度是長度，比率是比率，二者蓋有别。比率是‘數’，長度是‘度’。史公原文，一有‘長’字，如云‘黄鐘長八寸十分一，太簇長七寸十分二’，此長度也。一無‘長’字，如云‘九九八十一以爲宫，三分去一，五十四以爲徵’，此數也。《吕覽》《淮南》皆云黄鐘長九寸，此言八寸十分一者，蓋如小司馬所謂‘律九九八十一，故云長八寸十分一’也。此皆顯然不是‘實積數’。”[9]
以上即是司馬貞、蔡元定、王元啓、丘瓊蓀等爲主要代表的“九進制”、“十進制”合用説。
沈括《夢溪筆談》嘗云：“《史記·律書》所論二十八舍、十二律，多皆臆配，殊無義理。至於言數，亦多差舛。……律有多寡之數，有實積之數，有短長之數，有周徑之數，有清濁之數。其八十一、五十四、七十二、四十八、六十四，止是實積數耳。又云：‘黄鐘長八寸七分一，大吕長七寸五分三分一，太簇長七寸七分二，夾鐘長六寸二分三分一，姑洗長六寸七分四，中吕長五寸九分三分二，蕤賓長五寸六分二分一，林鐘長五寸七分四，夷則長五寸四分三分二，南吕長四寸七分八，無射長四寸四分三分二，應鐘長四寸二分三分二。’此尤誤也。此亦實積耳，非律之長也。蓋其間字又有誤者，疑後人傳寫之失也。餘分下分母凡‘七’字皆當作‘十’字，誤屈其中畫耳。黄鐘當作‘八寸十分一’，太簇當作‘七寸十分二’，姑洗當作‘六寸十分四’，林鐘當作‘五寸十分四’，南吕當作‘四寸十分八’。凡言七分者，皆是十分。”[10]
錢塘《史記三書釋疑》云：“九九八十一者，律之積數。……黄鐘實積八百十分（立方分——引者注，下同），以是爲宫而求徵、商、羽、角，其損益者皆積數也。律體圓如柱體，積八百十分（立方分），則面冪必九分（平方分——引者注），以冪除積而得九寸之長。……黄鐘之積八百一十分（立方分），約之而爲八十一分（立方分），……是分（立方分）有十分（立方分）也。”[11]
今人黄大同《千年聚訟的〈史記·律書〉律數考》一文辨此説：“否定了前人‘九分之寸法’的沈括，早已以定性爲管積的‘實積之數’説，給《史記·律書》的這一組律數究竟應該闡釋爲何數的問題，基本畫上了句號。沈括之後的歷代探索，大多追尋小司馬的思路，將這組律數視作本質爲數字律數的管長分數以十約成的管長寸數，即間接的管長之數，然其説明顯不如沈括的‘實積之數’説更爲合理。”[12]
以上即是沈括、錢塘、黄大同等爲主要代表的“實積”説。
司馬貞、蔡元定、王元啓等人認爲，漢代律數的計算有“九分之寸”的九進制和“十分之寸”的十進制兩法。第一組律數，如“九九八十一”，是黄鐘長“九寸”依九進制（一寸爲九分）换算成以寸、分之分爲單位的律數，其計量單位“分”隱而不顯。第二組律數，如黄鐘長“八寸十分一”，是將第一組以“分”爲單位的律數“九九八十一分”再依十進制（十分爲一寸）换算而成的以“寸”爲單位的律數，即第二組律數之“八寸十分一”，是黄鐘長“九寸”依九進制换算成以“分”爲單位的第一組律數之“九九八十一分”之後，再依十進制换算爲以“寸”爲單位的律數“八寸十分一”（八寸又十分之一寸），這個黄鐘長“八寸十分一”是“九寸”依九進制、十進制作兩次轉化而成的間接長度。第一組律數採用九進制，並以隱而不顯的“分”爲計量單位。第二組律數是將第一組以“分”爲計量單位的律數依十進制轉化成“寸”數。第一、二兩組律數爲九進制、十進制的混合産物。黄鐘之“九寸”、“八寸十分一”，兩數性質相同（同表長度），但來源不同（八寸十分一爲九寸的兩次轉化）。
沈括、錢塘等人將兩組律數統稱爲“實積之數”，不表長度，而是表實積（律管容積）。第一組律數爲比例數，第二組律數爲真正的實積數。沈括、錢塘等人看來，黄鐘長九寸，表長度，爲“長短之數”，而黄鐘長八寸十分一，表管積，爲“實積之數”，是管長（高）與管圍（面冪、底面積）相乘而得之數，與“長短之數”的性質、來源均不同。
我們不讚同沈括、錢塘等人的解釋，因爲兩組律數若均表示實積，則第二組律數與真實值不符，且兩組律數亦不能契合。我們以黄鐘“九九八十一以爲宫”爲例，實積爲管長（高）乘管圍（管圍即底面面冪，九平方分[13]）：9寸×9（平方）分＝9寸×0．09（平方）寸＝90分×9（平方）分＝0．81立方寸＝810立方分。
第一組律數之“八十一”代表0．81立方寸或810立方分，故“八十一”爲比例數，非真正的實積數，實積數是0．81立方寸或810立方分，故錢塘始有“黄鐘之積八百一十（立方）分，約之而爲八十一（立方）分……是（立方）分有十（立方）分”之説，已見前引。
今考《漢書·律曆志上》曰：“天之數始於一，終於二十有五。其義紀之以三，故置一得三，又二十五分之六，凡二十五置，終天之數，得八十一，以天地五位之合終於十者乘之，爲八百一十分，應曆一統千五百三十九歲之章數，黄鐘之實（實積——引者注）也。”[14]《律吕成書》“復以半周、半徑求黄鐘冪、積元數法”條云：“九平方分是爲黄鐘面冪，……八百一十立方分是爲黄鐘積實（即實積——引者注）。”[15]同卷“求黄鐘積實、面冪法”條云：“古法，黄鐘積實八百一十分（立方分——引者注，下同），今據前氣應之管其長九十分之分爲凖以度之，凡一分管長知空圍中當積九立方分，十分管長空圍中當積九十立方分，九十分管長則空圍中當積八百一十立方分，是爲黄鐘之積實也。凡論黄鐘管内積分（實積、容積——引者注）者，宜取方分（立方分），而《漢志》止言積實八百一十分者，省文耳。既得積實之數，如此知管面深一分則空圍中的容九方分（平方分）無疑，是又黄鐘之面冪也。”[16]《律吕新書》（黄鐘）“長九寸，空圍九分（平方分——引者注，下同），積八百一十分（立方分）”條云：“黄鐘之廣與長及空圍内積實皆可計，面冪計九方分（平方分），深一分管則空圍内當有九立方分，深九十分管計九寸，則空圍内當有八百一十立方分，此即黄鐘一管之實（實積——引者注）。其數與天地造化無不相合。”[17]又“虚”條云：“黄鐘之管長九十黍之廣，積九寸，度之所由起也；容千二百黍，積八百一十分（立方分——引者注），量之所由起也；重十有二銖，權衡之所由起也。”[18]皆可證我們計算出黄鐘律管實積（容積）爲810立方分（0．81立方寸）不誤。
第二組律數，例如黄鐘長“八寸十分一”，若如沈括、錢塘之説爲“實積耳，非律之長”，則“八寸十分一”（八立方寸又十分之一立方寸之省稱，古人用寸、分表長度之外，亦常用來表示方寸、方分，包括面積之平方寸、平方分和容積之立方寸、立方分[19]）即8．1立方寸或8100立方分，這與真實實積數（0．81立方寸或810立方分）不符，相差十倍，亦與其相應的第一組律數之“八十一”（比例數，代表0．81立方寸或810立方分）不能契合，此組律數不能表示實積。
若認定兩組律數表律管面積（即側面積，并假設底面周長爲九分），是否可以呢？今仍以黄鐘“九九八十一以爲宫”爲例，側面積爲管長（高）乘底面周長。我們計算：9寸×9分＝9寸×0．9寸＝90分×9分＝8．1平方寸＝810平方分。
第一組律數之“八十一”仍爲比例數，代表8．1平方寸或810平方分。第二組律數之黄鐘長“八寸十分一”（八平方寸又十分之一平方寸）即8．1平方寸或810平方分，與真實值相符，且與其相應的第一組律數之“八十一”能契合。那麽，是不是由此可以認爲兩組律數有表示律管面積的可能呢？
《漢書·律曆志上》云：“一曰備數，二曰和聲，三曰審度，四曰嘉量，五曰權衡。參五以變，錯綜其數，稽之於古今，效之於氣物，和之於心耳，考之於經傳，咸得其實，靡不協同。數者，一、十、百、千、萬也，所以算數事物，順性命之理也，本起於黄鐘之數。聲者，宫、商、角、徵、羽也，五聲之本，生於黄鐘之律。度者，分、寸、尺、丈、引也，所以度長短也，本起黄鐘之長。量者，龠、合、升、斗、斛也，所以量多少也，本起於黄鐘之龠，用度數審其容。衡權者，衡，平也，權，重也，衡所以任權而均物平輕重也；權者，銖、兩、斤、鈞、石也，所以稱物平施，知輕重也，本起於黄鐘之重；權與物鈞而生衡。”[20]《後漢書·律曆上》云：“古之人論數也，曰‘物生而後有象，象而後有滋，滋而後有數’。然則天地初形，人物既著，則算數之事生矣。記稱大橈作甲子，隸首作數。二者既立，以比日表，以管萬事。夫一、十、百、千、萬，所同用也；律、度、量、衡、曆，其别用也。故體有長短，檢以度；物有多少，受以量；量有輕重，平以權衡；聲有清濁，協以律吕；三光運行，紀以曆數：然後幽隱之情，精微之變，可得而綜也。”[21]《律吕新書》引《國朝會要》云：“古者，黄鐘爲萬事之根本，故尺、量、權衡皆起於黄鐘。”[22]今據此知，與黄鐘律有關者，爲數、聲、度（長短）、量（容積）、權（重量），但無表示面積之單位。這也是沈括只説“律有多寡之數，有實積之數，有短長之數，有周徑之數，有清濁之數”，没有提到與面積有關之數的原因。第二組律數之黄鐘長“八寸十分一”不可能表示黄鐘律管之面積。
第二組律數各具體數字前均有一“長”字，此亦表明該組律數不當表示律管之實積，亦不能表示律管之面積，只當表示律管之長度，故而司馬貞、蔡元定、王元啓爲主要代表的“九進制”、“十進制”合用説較爲合理。
今仍以黄鐘（宫）爲例，第一組律數之“九九八十一以爲宫”，依九進制，即：9寸×9＝81分。所謂“八十一”，即81分，爲實數，不是比例數。再依十進制：81分÷10＝8．1寸。此即第二組律數之黄鐘長“八寸十分一”，亦即八寸又十分之一寸，也即8．1寸或81分，這與其相應的第一組律數之“八十一”（實數，8．1寸或81分）契合。漢代是否九進制、十進制合用呢？《淮南子·天文篇》曰：“以三參物，三三如九，故黄鐘之律九寸而宫音調。因而九之，九九八十一，故黄鐘之數立焉。”[23]此爲九進制。《漢書·律曆志上》曰：“一爲一分，十分爲寸，十寸爲尺，十尺爲丈，十丈爲引。”[24]此爲十進制。兩制確實在合用。
《律吕正論》“第一算·縱黍八十一分律”條云：“黄鐘縱黍律長九寸，每寸九分，以九分乘九寸（自注：此謂九分之寸），得八寸十分一（自注：此謂十分之寸）。八寸十分一，猶言八十一分也。以九分乘九寸而得八寸一分，此與尋常定位不同，文義高古，不獨儒者難曉，雖善算者定位亦難。”[25]又“第二算·斜黍九十分律”條云：“黄鐘斜黍律長九寸，每寸十分，以十分乘九寸，得九十分。”[26]又“第三算·横黍一百分律”條云：“黄鐘横黍律長十寸，每寸十分，以十分乘十寸，得一百分。”[27]《律吕闡微》“律尺”條云：“古人算律有四種法：其一，以黄鐘爲十寸，每寸十分，共計百分；其二，以黄鐘爲九寸，每寸十分，共計九十分；其三，以黄鐘爲八十一分，不作九寸；其四，以黄鐘爲九寸，每寸九分，共計八十一分。一切算術皆取法於《河圖》《洛書》。《河圖》，十位，天地之體數也；《洛書》，九位，天地之用數也。是故算律之術：或有約十而爲九者，著其用也；或有約九而爲十者，存其體也。”[28]朱氏、江氏兩人雖非特定於《律書》而發此論，然其將古籍中黄鐘律數之所以有不同的記載均歸因於九進制、十進制算法不同。要之，此乃古人之主流觀點，正確、可取。
第一、二兩組律數如何而來？考《吕氏春秋·音律篇》曰：“黄鐘生林鐘，林鐘生太簇，太簇生南吕，南吕生姑洗，姑洗生應鐘，應鐘生蕤賓，蕤賓生大吕，大吕生夷則，夷則生夾鐘，夾鐘生無射，無射生仲吕。三分所生，益之一分以上生；三分所生，去其一分以下生。”[29]《淮南子·天文篇》曰：“黄鐘爲宫，下生林鐘。林鐘上生太簇。太簇下生南吕。南吕上生姑洗。姑洗下生應鐘。應鐘上生蕤賓。蕤賓上生大吕。大吕下生夷則。夷則上生夾鐘。夾鐘下生無射。無射上生仲吕。仲吕極不生。下生者倍，以三除之；上生者四，以三除之。”[30]《史記·曆書》曰：“黄鐘爲宫，林鐘爲徵，太簇爲商，南吕爲羽，姑洗爲角。”[31]司馬貞《索隱》云：“五聲之數亦上生三分益一，下生三分去一。宫下生徵，徵益一上生商；商下生羽，羽益一上生角。”[32]《漢書·律曆志上》曰：“五聲之本，生於黄鐘之律。九寸爲宫，或損或益，以定商、角、徵、羽。”[33]《宋書·律曆上》曰：“律吕相生，皆三分而損益之。……凡三分益一爲上生，三分損一爲下生。”[34]《律書》曰：“以下生者，倍其實，三其法。以上生者，四其實，三其法。”[35]瀧川資言云：“倍其實，三其法者，算家所謂
也。……四其實，三其法者，算家所謂
也。”[36]
我們在明白十二律及五聲上生、下生次序以及上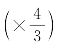生
、下生
方法後，便可知兩組律數原是依三分損益法産生：首先，依九進制，9寸×9＝81分，以81（分）即“八十一”爲首數，按照三分損益法産生第一組律數；其次，再依十進制，81分÷10＝8．1寸，以8．1（寸）即“八寸十分一”（八寸又十分之一寸）爲首數，按照三分損益法産生第二組律數。
今將第一組律數進行推算（計算一）：9寸×9＝81分（宫）；81分－81分×
＝81分×
＝54分（徵）（宫下生徵）；54分＋54分×
＝54分×
＝72分（商）（徵上生商）；72分－72分×
＝72分×
＝48分（羽）（商下生羽）；48分＋48分×
＝48分×
＝64分（角）（羽上生角）。
今將第二組律數進行推算（計算二）：黄鐘：81分（81分÷10＝8．1寸）；黄鐘下生林鐘：81分×
＝54分；林鐘上生太簇：54分×
＝72分；太簇下生南吕：72分×
＝48分；南吕上生姑洗：48分×
＝64分；姑洗下生應鐘：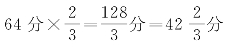
；應鐘上生蕤賓：
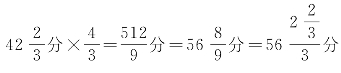；蕤賓上生大吕：
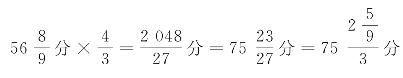；大吕下生夷則：
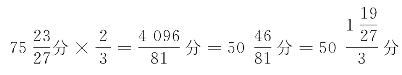；夷則上生夾鐘：
；夾鐘下生無射：
；無射上生仲吕：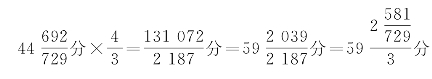
。
十二律數表
（续表）
今已將計算結果列表如上。第二組律數中的各具體數字（律數四）實乃真實律數（律數一）分子取整的結果，即取寸、分、釐數，而釐數下的毫、絲、忽、微等數則不取，此乃《律書》有意識的處理。那麽，爲何要這樣處理呢？因爲第二組律數是以首數“八寸十分一”（八寸又十分之一寸，8．1寸）按照三分損益法産生
，但三分損益存在一個問題，那就是所有的相生之數，因爲要三分，按照下生、上生計算出的最終結果，不可能都被整除，也就是説會出現無限位小數存在的情况。這種情况下，應作何取捨呢？《律書》作者就是將計算出的結果截取至釐數，按照這一取數原則，得到的就是如今我們計算出的結果。
我們通過算理證明了黄鐘長“八寸七分一”當校改爲“八寸十分一”，亦證明了歷代校勘家校“七分”作“十分”無誤。因爲只有如此校改，始能使十二律數符合三分損益。
夷則一律“五寸三分二”當訂正爲“五寸零分三分一”。今本《史記》的底本（即金陵局本）將夷則律數刻作“五寸四分三分二”，而點校人員認爲“四分”爲衍文，删衍之後作“五寸三分二”，但不確。因爲“五寸三分二”（五寸又三分之二寸）與“五寸零分三分一”（五寸零分又三分之一分）不相等，今人多有混淆者，[37]故特辨明之。古籍中的“零”多用“□”表示，金陵局本《史記》將夷則律數刻作“五寸四分三分二”，此“四”字實是將“零”鈔（刻）作“□”後在版本上的形譌。
今本《史記·律書》餘外十個律數皆正確無誤。
第二組律數，宫、商、角、徵、羽五聲與十二律相配有譌誤。上述梁玉繩引《史詮》曰“太簇‘角’當作‘商’，姑洗‘羽’當作‘角’，林鐘‘角’當作‘徵’，南吕‘徵’當作‘羽’。俱後人傳寫之誤”，其説甚是。今據律數應是：黄鐘（八寸十分一）——宫（八十一）；太簇（七寸十分二）——商（七十二）；姑洗（六寸十分四）——角（六十四）；林鐘（五寸十分四）——徵（五十四）；南吕（四寸十分八）——羽（四十八）。《史記·曆書》曰“黄鐘爲宫，林鐘爲徵，太簇爲商，南吕爲羽，姑洗爲角”，已見前引。今又考《淮南子·天文篇》曰：“凡十二律，黄鐘爲宫，太簇爲商，姑洗爲角，林鐘爲徵，南吕爲羽。”[38]
仲吕下有徵，夷則下有商，應鐘下有羽，此“徵”、“商”、“羽”三字當爲衍文。《律吕新書》云：“仲吕下有‘徵’，夷則下有‘商’，應鐘下有‘羽’字，三者未詳，疑後人誤增也。”[39]王元啓曰：“仲吕下‘徵’字，夷則下‘商’字，直當定爲衍文，删去，庶可稍通。……‘應鐘長四寸二分三分二，羽’，‘羽’字衍。”[40]今考《漢書·律曆志上》有云：“黄鐘爲宫，則太簇、姑洗、林鐘、南吕皆以正聲應，無有忽微，不復與它律爲役者，同心一統之義也。非黄鐘而它律，雖當其月自宫者，則其和應之律有空積忽微，不得其正。此黄鐘至尊，亡與並也。”[41]顔師古引孟康曰：“忽微，若有若無，細於髮者也。謂正聲無有殘分也。”[42]黄鐘（宫）、太簇（商）、姑洗（角）、林鐘（徵）、南吕（羽）皆爲“正聲”，亦即“無有殘分”，這與其各自律數之八寸十分一（八十一分）、七寸十分二（七十二分）、六寸十分四（六十四分）、五寸十分四（五十四分）、四寸十分八（四十八分）皆無殘分適相契合。有殘分的仲吕下之“徵”，夷則下之“商”，應鐘下之“羽”，三字爲衍文。
今本《史記·律書》“律數”一節，其文當修正如下：九九八十一以爲宫。三分去一，五十四以爲徵。三分益一，七十二以爲商。三分去一，四十八以爲羽。三分益一，六十四以爲角。黄鐘長八寸十分一，宫。大吕長七寸五分三分二。太簇長七寸十分二，商。夾鐘長六寸七分三分一。姑洗長六寸十分四，角。仲吕長五寸九分三分二。蕤賓長五寸六分三分二。林鐘長五寸十分四，徵。夷則長五寸□分三分一。南吕長四寸十分八，羽。無射長四寸四分三分二。應鐘長四寸二分三分二。
今修訂本《史記·律書》“律數”之文曰：“九九八十一以爲宫。三分去一，五十四以爲徵。三分益一，七十二以爲商。三分去一，四十八以爲羽。三分益一，六十四以爲角。黄鐘長八寸七分一，宫。大吕長七寸五分三分一。太簇長七寸七分二，角。夾鐘長六寸一分三分一。姑洗長六寸七分四，羽。仲吕長五寸九分三分二，徵。蕤賓長五寸六分三分一。林鐘長五寸七分四，角。夷則長五寸四分三分二，商。南吕長四寸七分八，徵。無射長四寸四分三分二。應鐘長四寸二分三分二，羽。”[43]
修訂本《史記·律書》篇末“校勘記”曰：“黄鐘長八寸七分一。七，《索隱》本、殿本作‘十’。黄鐘長八寸七分一之‘七’，沈括、蔡元（定）、王元啓、張文虎皆以爲當依《索隱》作‘十’。與此相應，本篇所載律數，唐代司馬貞《索隱》已疑其誤，宋代沈括《夢溪筆談》、蔡元（定）《律吕新書》繼起考辨，清代錢大昕《考異》、梁玉繩《志疑》、王元啓《正譌》等多有考證，張文虎《札記》亦有申論，諸家考辨校改凡八處。董樹巖、戴念祖、羅琳《〈史記·律書〉律數匡正——兼論先秦管律》指出：經過嚴格推算可以認定，《律書》所載不是弦律，而是管律，其資料基本無誤，各家考辨誤以爲弦律而加以推算校勘，結論有誤。《隋書》卷一六《律曆志上》：‘傳稱黄帝命伶倫斷竹，長三寸九分，而吹以爲黄鐘之宫，曰含少。次制十二管，以聽鳳鳴，以别十二律，比雌雄之聲，以分律吕。上下相生，因黄鐘爲始。《虞書》云：“叶時月正日，同律度量衡。”夏禹受命，以聲爲律，以身爲度。《周禮》，樂器以十二律爲之度數。司馬遷《律書》云：“黄鐘長八寸七分之一，太簇長七寸七分二，林鐘長五寸七分三，應鐘長四寸三分二。”此樂之三始，十二律之本末也。’《隋志》所引，與今本《史記》大致相同，而與各家校改格格不入。今一仍其舊。”[44]引張文虎《校刊史記集解索隱正義札記》曰：“‘七’字誤。《索隱》本作‘十’，是。然云舊本多作‘七分’，則承譌久矣。”[45]文字的處理是“一仍其舊”，保留了底本《史》文原貌。
董樹巖、戴念祖、羅琳合撰《〈史記·律書〉律數匡正——兼論先秦管律》一文，對於該文的結論，今有商榷的必要。
董、戴、羅氏三人在其文章中經過一番討論，認爲《史記·律書》中的“律數”是經過管口校正的管律數據，並將《律書》“律數”第二組數字校正如下：黄鐘長八寸七分一；大吕長七寸五分三分一，校作八寸一分二；太簇長七寸七分二；夾鐘長六寸一分三分一，校作七寸一分三分一；姑洗長六寸七分四；仲吕長五寸九分三分二，校作六寸三分二；蕤賓長五寸六分三分一，校作五寸九分三分二；林鐘長五寸七分四，校作五寸六分三分二；夷則長五寸四分三分二，校作五寸二分三分二；南吕長四寸七分八，校作四寸九分八；無射長四寸四分三分二，校作四寸六分三分二；應鐘長四寸二分三分二，校作四寸三分三分二。[46]
這種校改對《律書》“律數”一節的數字變動甚大，只有黄鐘、太簇、姑洗三律仍其舊，而大吕、夾鐘、仲吕三律則將寸數改動，又將林鐘一律多出釐數，剩下的蕤賓、夷則、南吕、無射、應鐘五律亦有比較大的改動（即數字間的校改無迹可尋，如很難看作因形近而誤，等等），這種校改距離《律書》的原貌相差太遠，恐《律書》原文不至有如此之大誤。董氏三先生的校改只是爲了證明黄鐘、太簇、姑洗三律原作“七分”不誤，爲此却改動另外的所有律數來遷就此三律，大有削足適履之感。
黄大同説：“在《〈史記·律書〉律數匡正——兼論先秦管律》一文作者的十二律校正之數中，連同生律首數黄鐘僅有三律與《史記·律書》中的該組數據相同，其餘九律相異，並且這些相異之數散亂無序，之間未表現出任何有聯繫的規律現象來，這與‘九分之寸法’和‘實積之數’兩説，在改‘七’爲‘十’的校勘中所體現出來的規律性完全不能比擬。因而僅從概率的角度看，《史記·律書》中的這一組律數是先秦‘經過管口校正的管律數據’的可能性也應予以排除。”[47]修訂本《史記》爲謹慎起見，只採用董氏三人之黄鐘、太簇、姑洗三律作“七分”的校勘結果，作爲保留底本文字原貌的依據，但對於他們餘外律數的校改則没有採用，亦見此三人的校改難以使學者完全信服。
《律書》“律數”一節，究竟是管律還是弦律，對各個具體律數數字並不存在影響。因爲這兩組律數按照三分損益法産生，關鍵在於首數，只要首數確定，按照三分損益法相生，後面的各個具體律數數字都有其自身的固定值。十二個律數就是一個有機整體，只要其中某個律數發生了變動，其餘十一個律數都必須作出相應的調整，以便使十二律數符合三分損益。
胡企平曾在《“黄鐘長八寸七分一”是先秦管律中完全正確的黄鐘宫音管長嗎？——與戴念祖先生〈先秦管律的可能性〉[48]一文中所據以校改的觀點商榷》的實驗性文章中，通過必要的“制管驗聲”這一實驗性手段加以驗證，以“實驗報告”的形式將有關數據和結果呈現給大家。胡氏在其文“實驗報告”的“小結”中説：“無論從測音實驗後的音響高下事實，還是從分析推理來看，舊本《史記·律書》所記述的‘黄鐘長八寸七分一，宫’不是先秦管律中正確的黄鐘宫音管長。既然‘皮之不存，毛將焉附’？因此，他們（謂《〈史記·律書〉律數匡正——兼論先秦管律》——引者注）所推算出的‘管律十二律’，以及所提供的‘管口校正數’，根本就是無稽之談。”[49]在其文最後的“結論”中重新加以歸結，説：“筆者認爲，可以肯定的説《史記》中所謂‘八寸七分一’的黄鐘律管是不存在的。究其‘十’成爲‘七’的原因：一因往昔暴秦焚書，先秦之管律於漢代已經失傳，自時厥後，後人因舊文之遺殘，在删補時往往增損其語所致；二係後人傳寫之誤。它非先秦管律中正確的黄鐘宫音管長，歷代校勘家改‘七’爲‘十’是正確的，而所校改成的‘八寸十分一’符合司馬遷撰《史記·律書》中這組弦律三分損益律數之本意。”[50]胡氏之文，其方法雖與我們不同，然其結論則與我們深相契合。
《隋書·律曆志上》引《史》文雖作“七分”，但《隋志》所據《史》本，恐即是司馬貞所云“舊本”[51]，《隋志》文字當是承誤本《史記》而來。我們仍堅持“七分”當作“十分”，因爲只有如此，十二律數才能符合三分損益。
今有必要談談《史記·律書》“律數”爲何要合用九進制、十進制。
如若《律書》“律數”不合用九進制、十進制先將黄鐘長“九寸”轉换爲“八寸十分一”，而是徑直以“九寸”作三分損益相生，其前五律，即五聲所主之律，應爲（計算三）：黄鐘（宫）：9寸；黄鐘（宫）下生林鐘（徵）：
；林鐘（徵）上生太簇（商）：6寸×
＝8寸；太簇（商）下生南吕（羽）：
；南吕（羽）上生姑洗（角）：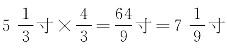
。因第一組律數爲黄鐘長“九寸”依九進制换算成以“分”爲單位，今再依九進制回算成以“寸”爲單位表直接長度的律數（計算四）：宫（黄鐘）：81分÷9＝9寸；徵（林鐘）：54分÷9＝6寸；商（太簇）：72分÷9＝8寸；羽（南吕）：48分÷9＝
；角（姑洗）：64分÷9＝
。計算結果乃爲前五律直接長度，此與《律書》第二組“律數”表示的間接長度（見計算二）不同。
今考《後漢書·律曆上》劉昭引鄭玄曰：“宫數八十一，黄鐘長九寸，九九八十一也。三分宫去一生徵，徵數五十四，林鐘長六寸，六九五十四也。三分徵益一生商，商數七十二，太簇長八寸，八九七十二也。三分商去一生羽，羽數四十八，南吕長五寸三分寸之一，五九四十五又三分寸之一，爲四十八也。三分羽益一生角，角數六十四，姑洗長七寸九分寸之一，七九六十三又九分寸之一，爲六十四也。”[52]其“三分去一”即下生，“三分益一”即上生，鄭氏之説可證我們的計算不誤。
《律書》“律數”一節，之所以要合用九進制、十進制，是因爲只有將黄鐘長“九寸”先依九進制轉换爲“八十一”（九九八十一，81分），再依十進制换算成“八寸十分一”（八寸又十分之一寸，8．1寸）之後，始能保證依三分損益法相生之前五律，即五聲所主之律，其律數全部爲整數，無殘分（參見計算二），即：宫——黄鐘——八十一（分）——八寸十分一；徵——林鐘——五十四（分）——五寸十分四；商——太簇——七十二（分）——七寸十分二；羽——南吕——四十八（分）——四寸十分八；角——姑洗——六十四（分）——六寸十分四。這種整齊而無殘分的現象，即前引《漢書·律曆志上》所謂“黄鐘爲宫，則太簇、姑洗、林鐘、南吕皆以正聲應，無有忽微”，寓有“同心一統”、“黄鐘至尊，亡與並”之意。如果“律數”一節不合用九進制、十進制先將黄鐘長“九寸”轉换爲“八寸十分一”，而是徑直以“九寸”據十進制作三分損益相生，其前五律（五聲所主之律）不能全部爲整數，會有殘分（參見計算三），即：羽——南吕——
——
；角——姑洗——
——
。如此，南吕、姑洗兩律因有殘分而致其不能“以正聲應，無有忽微”，便不能表現出“同心一統”、“黄鐘至尊，亡與並”之大義。
曆書第四
名察度驗。（4/1260/11）
《漢志》作“名察發驗”。（2/766/6）
按：梁氏止出列《史》《漢》異文，因無所裁斷，故爲之補説。
考此《曆書》曰：“蓋聞昔者黄帝合而不死，名察度驗，定清濁，起五部，建氣物分數。然蓋尚矣。書缺樂弛，朕甚閔焉。朕唯未能循明也，紬績日分，率應水德之勝。今日順夏至（謂夏至及冬至——引者注），黄鐘爲宫，林鐘爲徵，太簇爲商，南吕爲羽，姑洗爲角。自是以後，氣復正，羽聲復清，名復正變，以至子日當冬至，則陰陽離合之道行焉。”[53]裴駰《集解》引臣瓚曰：“題名宿度，候察進退，謂三辰之度，吉凶之驗也。”[54]司馬貞《索隱》曰：“《漢書》作‘名察發歛’。韋昭云：‘發，氣發；歛，氣歛。’又《續漢書》以爲道之發歛，景之長短，則發歛是日行道去極盈縮也。”[55]又考《漢書·律曆志上》曰：“蓋聞古者黄帝合而不死，名察發斂，定清濁，起五部，建氣物分數。”[56]顔師古引孟康曰：“春夏爲發，秋冬爲斂。”[57]
《史》《漢》“度驗”、“發斂”，當以何者爲是呢？
方苞辨此曰：“名察者，五星二十八宿之名於是而辨也；度驗者，其宿離遲速之度皆可驗也。”[58]王元啓曰：“名察度驗猶言察名驗度，謂察諸星宿之名，驗其廣狹之度也。”[59]二人乃是據《曆書》“名察度驗”四字立説，其解頗相類，然未敢信從。《曆書》作“度驗”，恐有譌誤，當從《漢志》作“發斂”。王念孫辨《曆書》之文，引王引之曰：“名察度驗，《漢志》作‘名察發斂’。應劭曰：‘名節會，察寒暑，致啓閉分至。’孟康曰：‘春夏爲發，秋冬爲斂。’晉灼曰：‘蔡邕《天文志》渾天名察發斂，以行日月，以步五緯。’又《周髀算經》：‘冬至、夏至者，日道發斂之所生也。’趙君卿曰：‘發猶往也，斂猶還也。’則當作‘發斂’爲是。《史記》作‘度驗’者，發字，古通作廢，其草書與‘度’相似，又涉上文‘星度’而誤耳。斂、驗，聲相近，故字亦相通。下文曰：‘今日順夏至，黄鐘爲宫，林鐘爲徴，太簇爲商，南吕爲羽，姑洗爲角。自是以後，氣復正，羽聲復清，名復正變，以至子日當冬至，則陰陽離合之道行焉。’是律之清濁，出於氣之發斂，故曰‘名察發斂，定清濁’，無取於度驗也。薛瓚以爲‘題名宿度，候察進退’，乃不得其解而曲爲之説。”[60]則知《曆書》“度驗”二字，蓋本作“廢驗”，猶《漢志》“發斂”也。梅文鼎曰：“發斂二字，乃日道發南斂北之謂。蓋主乎北極爲言，則夏至近極爲斂，冬至遠極爲發。而自冬至以至夏至，則由遠而近，自夏至以至冬至，則由近而遠，總謂之發斂。古諸家曆法皆以‘發斂’另爲一章，其中所列爲二十四氣、七十二候之類，而加時之法附焉，故曰‘發斂加時’。”[61]王玉樹曰：“歲有分、至、啓、閉，察其日躔發斂焉。分謂春分、秋分，至謂冬至、夏至，啓謂立春、立夏，閉謂立秋、立冬，是謂八節。夏至日極北，以後漸向南，至秋分南北中，至冬至而南極，極則復向北，至春分而中，夏至而復北極。自南而北爲斂，自北而南爲發。發斂一終，而歲成焉。”[62]所謂“發斂”者，即往還、進退，乃謂日道發南斂北，察發斂以定節氣。《漢志》“名察發斂”，王先謙引周壽昌據《後漢書》云：“道之發斂：日道發南，去極彌遠，其景彌長，遠長乃極，冬乃至焉；日道斂北，去極彌近，其景彌短，近短乃極，夏乃至焉。”[63]沈欽韓引《明史》曰：“古曆以‘發斂’爲一章。日道發南斂北之細數也。”[64]沈氏又曰：“冬至後，日行南陸爲發；夏至後，日行北陸爲斂。”[65]今從此説。
天官書第五
中宫天極星。（4/1289/7）
《史記考異》曰：“此中宫及東宫、南宫、西宫、北宫五‘宫’字皆當作‘官’，下文云‘天之五官坐位’，可證史公本文皆作‘官’矣。”（2/767/34）
按：錢大昕之説未必可從，梁氏不當遽信之。
考此《天官書》曰：“中宫天極星，其一明者，太一常居也。”[66]司馬貞《索隱》引姚氏據《春秋元命包》云：“官之爲言宣也。宣氣立精爲神垣。”[67]用“宣”字訓“官”，似《史》文原作“官”字。
錢大昕辨此，嘗曰：“此中宫天極星及東宫蒼龍、南宫朱鳥、西宫咸池、北宫玄武，五‘宫’字皆當作‘官’。案：下文云：‘紫宫、房心、權衡、咸池、虚危，此天之五官坐位也。’可證史公本文皆作‘官’矣。《索隱》於‘中宫’下引《春秋元命包》：‘官之爲言宣也。’古卜取音義相協，展轉互訓，以宣訓官，音相近也。流俗本亦譌作宫，由於不知古音。下文‘紫宫’下乃引《元命包》：‘宫之言中也。’又可證小司馬元本中宫作中官矣。小司馬解‘天官’云：‘天文有五官。官者，星官也。星座有尊卑，若人之官曹列位，故曰天官。’”[68]
錢氏之論有誤。《天官書》“此天之五官坐位”，方苞曰：“官，當作‘宫’，即篇首所列五宫也。”[69]又《天官書》“紫宫”，《索隱》引《元命包》曰“宫之言中也”，適證小司馬原本當作“宫”字。今考《史記·秦始皇本紀》“（信宫）象天極”《索隱》引《天官書》曰：“中宫曰天極。”[70]可證《索隱》所見《史》本《天官書》作“中宫”。小司馬解“天官”曰：“天文有五官。官者，星官也。”乃是小司馬題解太史公《天官書》之語，自與中宫天極、東宫蒼龍、南宫朱鳥、西宫咸池、北宫玄武之五宫不同。考《漢書·天文志》稱中宫天極、東宫蒼龍、南宫朱鳥、西宫咸池、北宫玄武，[71]《漢志》五“宫”字皆不作“官”。《晉書·天文上》亦作“中宫”[72]，《隋書·天文上》同，[73]皆可證作“宫”字者爲是。
王叔岷引高平子曰：“清儒（錢大昕）以爲‘宫’當作‘官’，然《天官書》雖以天官命星座，而分全天星官爲中、東、南、西、北等五大區，以每區爲一宫，其義甚順，‘官’字未必更當。中宫下接天極星者，以天極星爲中宫之主要星座也。”[74]
李人鑒辨此甚詳，其言曰：“《漢書·天文志》諸‘宫’字皆不作‘官’。其篇首云：‘凡天文在圖籍昭昭可知者，經星常宿中外官凡百一十八名，積數七百八十三星，皆有州國官宫物類之象。’《後漢書·天文志》云：‘斗、衡、太微、攝提之屬百二十官，二十八宿各布列，下應十二子。’《晉書·天文志》引張衡云：‘中外之官，常明者百有二十四，可名者三百二十，爲星二千五百，微星之數蓋萬有一千五百二十。’《天文志》又云：‘後武帝時，太史令陳卓總甘、石、巫咸三家所著星圖，大凡二百八十三官，一千四百六十四星，以爲定紀。’各書《天文志》言中外之官，或曰‘百一十八名’，或曰‘百二十官’，或曰‘百有二十四’，或曰‘二百八十三官’，雖不盡同，而皆未嘗有東官、西官、南官、北官、中官之稱，更未嘗有合稱此五者爲五官者。此書下文有‘此天之五官坐位也’一語，方苞《史記注補正》以爲‘官’當作‘宫’。觀《國語·楚語下》有‘五官’一語，而云：‘於是乎有天地神民類物之官，是謂五官。’《淮南子·天文訓》亦有‘五官’一語，而云：‘何謂五官？東方爲田，南方爲司馬，西方爲理，北方爲司空，中央爲都。’皆與各書《天文志》所云‘中外之官’迥非一事，是證史公此《書》初無‘中官、東官、南官、西官、北官’及‘五官’之稱。帝王所居，必在宫廷。故漢高祖未徙治長安時，居洛陽南宫，既徙治長安，則居於長樂宫。後又營作未央宫，而新豐復有新豐宫，沛亦有沛宫。天宇遼闊，衆宫布列，擬之人間，自當有宫廷以處之。故北辰所在，則有中宫，四方則有東宫、北宫、西宫、南宫。此絶不悖於情理，安得以爲非實，而必云諸‘宫’字皆‘官’字之誤乎？後人以天子宫廷，悉在京師，京師之外，雖亦有行宫之屬，似不得比於京師之宫廷也，故《晉書·天文志》第言中宫，餘則云東方、北方、西方、南方。而其中宫之稱，固本之於史公此《書》也。此亦可爲此篇之言中宫、東宫、南宫、西宫、北宫者非誤之明證矣。本書《高祖本紀》云：‘八年，蕭丞相營作未央宫，立東闕、北闕、前殿、武庫、太倉。’《集解》引《關中記》曰：‘東有蒼龍闕，北有玄武闕，玄武所謂北闕。’《索隱》云：‘東闕名蒼龍，北闕名玄武，無西南二闕者，蓋蕭何以厭勝之法故不立也。’《正義》云：‘北闕爲正者，蓋象秦作前殿，渡渭水屬之咸陽，以象天極閣道絶漢抵營室。’未央宫之營作，蓋仿天象爲之。未央宫猶之中宫。東有蒼龍闕，猶之此篇所云‘東宫蒼龍’也；北有玄武闕，猶之此篇所云‘北宫玄武’也。北闕爲正，渡渭水屬之咸陽，象天極閣道絶漢抵營室，即此篇中宫下所云‘紫宫後六星絶漢抵營室，曰閣道’、北宫下所云‘營室爲清廟，曰離宫、閣道’。觀此亦可知天人之間之相仿效處。未央之言宫闕，正猶此篇之先言中宫而依次及於東宫、北宫等，安得謂此篇‘宫’字誤，而以小司馬所見本之作‘官’字者爲是耶？此篇叙中宫諸天官時有‘皆曰紫宫’一語，是史公固以紫宫爲中宫也。環紫宫之十二星，後世稱爲紫微垣，而東宫亦有天市垣，南宫亦有太微垣。有宫始得有宫垣。據此亦可知史公此篇蓋本作中宫、東宫、南宫、西宫、北宫，而非作中官、東官、南官、西官、北官也。以有以上諸端，吾故以錢氏此篇‘宫’字當作‘官’之説爲不可信從也。”[75]
今考此《天官書》[76]：其“中宫天極星”句，《索隱》引《文耀鈎》曰：“中宫大帝，其精北極星。”又“東宫蒼龍”句，《索隱》引《文耀鈎》曰：“東宫蒼帝，其精爲龍。”又“南宫朱鳥”句，《索隱》引《文耀鈎》曰：“南宫赤帝，其精爲朱鳥。”又“西宫咸池”句，《索隱》引《文耀鈎》曰：“西宫白帝，其精白虎。”又“北宫玄武”句，《索隱》引《文耀鈎》曰：“北宫黑帝，其精玄武。”又“（東宫蒼龍）房、心”句，《索隱》引《春秋説題辭》曰：“房、心爲明堂，天王布政之宫。”又“（南宫朱鳥）太微”句，《索隱》引宋均曰：“太微，天帝南宫也。”《文耀鈎》既稱大帝、蒼帝、赤帝、白帝、黑帝，必不得目之爲中官、東官、南官、西官、北官矣。《春秋説題辭》、宋均之説，亦可證《天官書》原作“宫”字不誤。
其下之國，可以重致天下。禮、德、義、殺、刑盡失，而填星乃爲之動摇。（4/1320/4-5）
填星爲信，而仁、義、禮、智以信爲主，故以信爲重。《漢志》亦云“從填以重”也。“德”字當衍。“義”乃“仁”之誤，宜云“仁、禮、殺、刑盡失”，蓋歲星爲仁，熒惑爲禮，太白爲義，辰星爲智，殺即義，刑即智，故《漢志》云：“從太白以兵，從辰以法。”（2/775/4-6）
按：梁氏此説多有誤。
考此《天官書》曰：“義失者，罰出歲星。……五星皆從而聚於一舍，其（歲星——引者注）下之國可以義致天下。”[77]又曰：“禮失，罰出熒惑，熒惑失行是也。……五星皆從而聚於一舍，其（熒惑——引者注）下國可以禮致天下。”[78]又曰：“五星皆從而聚於一舍，其（填星——引者注）下之國可以重致天下。禮、德、義、殺、刑盡失，而填星乃爲之動摇。”[79]又曰：“殺失者，罰出太白。……五星皆從太白而聚乎一舍，其（太白——引者注）下之國可以兵從天下。”[80]又曰：“刑失者，罰出辰星。……五星皆從辰星而聚於一舍，其（辰星——引者注）所舍之國可以法致天下。”[81]則知歲星爲義，熒惑爲禮，太白爲兵，辰星爲法，殺即兵，刑即法。
《史》文“可以重致天下”句，原無“以”字，王念孫曰：“填星所居，五星皆從而聚於一舍，其下之國可以重致天下。今本脱‘以’字，上文歲星云‘可以義致天下’，熒惑云‘可以禮致天下’，下文太白云‘可以兵從天下’，辰星云‘可以法致天下’，今據補。《正義》曰：‘言五星皆從填星，其下之國倚重而致天下。’《漢書·天文志》：‘凡五星所聚宿，其國王天下，從歲以義，從熒惑以禮，從填以重，從太白以兵，從辰以法。’韋昭解‘從填以重’曰：‘謂以威重得。’念孫案：韋氏、張氏皆未曉‘重’字之義。重猶厚也。高誘注《秦策》及《吕氏春秋·振亂篇》並曰：‘厚，重也。’又注《吕氏春秋·盡數篇》及《淮南·俶真篇》並曰：‘重，厚也。’是厚、重二字同義。填星爲土，土德厚重，故五星從填星，則其下之國可以厚重之德致天下也。《開元占經·五星占》引《春秋運斗樞》曰：‘填星帥五精聚于中央，黄帝以重厚賢聖起。’又引《石氏星經》曰：‘填星所在五星皆從而聚於一舍，其下之國可以重德致天下。’（《天官書》即本於此，‘重’下無‘德’字者，省文耳。止文曰‘填星主德’，德即重德也）皆其明證矣。”[82]
王氏謂“重”下無“德”字者，乃省文，蓋不然。若是省文，則無以明其爲重德之義。《天官書》之文當同《石氏星經》，原作“可以重德致天下”。《隋書·天文下》作“必有重德致天下”[83]，是“重”字下當有“德”字。《天官書》下文曰“禮、德、義、殺、刑盡失”，此“德”字本當在上文“重”字下，今本誤衍在“禮”字下。《天官書》原只作“禮、義、殺、刑盡失，而填星乃爲之動摇”，禮謂熒惑，義謂歲星，殺謂太白，刑謂辰星，止此四星，故《漢書·天文志》曰：“四星皆失，填星乃爲之動。”[84]《晉書·天文中》亦云：“四星皆失，填乃爲之動。”[85]如若《天官書》原有“德”字，則爲五星而非四星矣。
填星爲德，不爲信。《天官書》云“禮、德、義、殺、刑盡失，而填星乃爲之動摇”，此“德”字雖爲衍文，但當補在上文“重”字之下，云“禮、義、殺、刑盡失”，前後承熒惑（禮）、歲星（義）、太白（殺、兵）、辰星（刑、法）四星而言，故“義”字亦非“仁”字之誤。歲星爲義，熒惑爲禮，太白爲兵，辰星爲法，殺即兵，刑即法。
中華書局修訂本《史》文亦補“以”字，甚是，但“德”字仍誤衍在“禮”字下。[86]
金爲白衣會若水。金在南曰牝牡，年穀熟。（4/1320/12）
“水”乃“木”之譌。《漢》、《晉》《志》作“爲水”，亦非。（2/775/14）
按：梁氏此説不可從。
《天官書》曰：“木星與土合，爲内亂，饑，主勿用戰，敗；水則變謀而更事；火爲旱；金爲白衣會若水。金在南曰牝牡，年穀熟。金在北，歲偏無。”[87]木與土合爲内亂，饑；木與水合爲變謀，更事；木與火合爲旱；木與金合爲白衣會及水事也。其“金在南曰牝牡”句，張守節《正義》引《星經》云：“金在南，木在北，名曰牝牡，年穀大熟；金在北，木在南，其年或有或無。”[88]
梁氏不知《史》文“若”字之義，讀“若水”二字屬下爲句，將“若水、金在南曰牝牡”作一句讀，又依《正義》引《星經》之説校“水”作“木”字，讀作“若木、金在南曰牝牡”。然而，經此校改，木位則與《星經》之説相反矣。
若水，義訓“及水”，上屬“白衣會”爲句，今本句讀不誤。王念孫曰：“‘若水’二字，文與上屬，不與下屬。金爲白衣會若水者，水謂水災也。《漢書·高祖紀》注曰：‘若，及也。’言木與金合，則爲白衣會及水災也。上文曰：‘填星失次下二三宿曰縮。有后戚，其歲不復。不，乃天裂若地動。’下文曰：‘月蝕歲星，其宿地饑若亡。’文義並與此同。《漢書·天文志》作：‘歲與太白合，則爲白衣之會爲水。’《開元占經·五星占》引巫咸曰：‘大白與歲星合，爲白衣之會爲水。’此皆其明證矣。”[89]瀧川資言引陳仁錫曰：“若，及也。言木與火合則爲旱，木與金合則爲國家喪及水澇也。”[90]《經傳釋詞》“若”字條嘗云：“若，猶及也。《書·召誥》曰：‘越五日甲寅，位成，若翼日乙卯。’言及翼日乙卯也。《吴語》越大夫種曰：‘王若今起師以會。’言及今起師以會戰也。故成二年《左傳》‘病未及死’，《晉語》作‘病未若死’。”[91]
《漢》、《晉》《志》作“爲水”，實亦不誤。
爲，訓及。考《史記·齊太公世家》曰：“田氏卒有齊國，爲齊威王，彊於天下。”[92]瀧川資言引中井積德曰：“威王是田和之孫，是文似混同，豈脱文邪？或曰：爲，字當作及。”[93]王叔岷曰：“爲，猶及也。此無脱文，無煩改字。”[94]今人蕭旭先生著有《古書虚詞旁釋》一書，其“爲”字條，一訓作“及”義，曰：“《韓子·難勢》：‘上不及堯舜，而下亦不爲桀紂。’《論衡·龍虚》：‘丘上不及龍，下不爲魚，中止其龜與？’上二例，爲、及互文。按，下例，《吕氏春秋·舉難》作‘下不若魚’。（爲、若，二字同，此即明證——引者注）……《莊子·至樂》：‘夫子貪生失理而爲此乎？將子有亡國之事、斧鉞之誅而爲此乎？將子有不善之行、愧遺父母妻子而爲此乎？將子有凍餒之患而爲此乎？將子之春秋故及此乎？’上四‘爲’字與‘及’異字同義。曹植《求通親親表》：‘伊尹耻其君不爲堯舜。’按，《文苑英華》卷六五一《重上直言諫東宫啓》：‘古人耻其君不及堯舜。’卷四一《高祖受命造唐賦》：‘耻其君不及唐堯。’可爲旁證。”[95]爲水，即若水、及水。
去地可六丈。（4/1333/14）
《漢志》云“大而黄”，與前後文“大而赤”、“大而白”相類，此缺“而黄”二字。或謂徐廣“大”一作“六”，則“大”字當提行，與下節“賊星”爲一句，觀《正義》稱“大賊星，一名六賊”可證。曰：以徐注指下節“賊星”，是也；以“大”字與“賊星”爲句，非也。蓋此自缺“而黄”二字，下節另脱“大”字，各本誤以徐注屬此耳。（2/782/15—783/2）
按：梁氏認爲《史》文缺“而黄”二字，當是，但又説下節另脱“大”字則非。
考此《天官書》曰：“五殘星，出正東東方之野。其星狀類辰星，去地可六丈。大賊星，出正南南方之野。星去地可六丈，大而赤，數動，有光。”[96]裴駰《集解》引徐廣曰：大賊星“大，一作六”[97]。張守節《正義》曰：“大賊星者，一名六賊，出正南，南方之野。”[98]梁氏讀“（五殘星）去地可六丈大”爲句，故有此論。
今本《天官書》“（五殘星）去地可六丈”下當脱“大而黄”三字，而“大賊星”之“大”字，當如徐廣所見，本作“六”字。《天官書》“（五殘星）去地可六丈大賊星”，錢大昕辨此曰：“大，當作六。‘六’字連下句讀。六賊，星名也。”[99]李人鑒曰：“‘賊星’上‘大’字，當據《漢志》《晉志》改作‘六’。”[100]或是“大賊星”之“大”字，上屬“去地可六丈”爲句，下脱“而黄”二字，下節“賊星”上另脱“六”字，即傳抄誤脱“而黄六”三字。
今考《天官書》曰：“國皇星，大而赤，狀類南極。所出，其下起兵，兵彊；其衝不利。昭明星，大而白，無角，乍上乍下。所出國，起兵，多變。五殘星，出正東東方之野。其星狀類辰星，去地可六丈。大賊星，出正南南方之野。星去地可六丈，大而赤，數動，有光。司危星，出正西西方之野。星去地可六丈，大而白，類太白。獄漢星，出正北北方之野。星去地可六丈，大而赤，數動，察之中青。此四野星所出，出非其方，其下有兵，衝不利。”[101]正東之五殘星，正南之大賊星（六賊星），正西之司危星，正北之獄漢星，是謂“四野星”。
《漢書·天文志》叙此“四野星”曰：“五殘星，出正東，東方之星。其狀類辰，去地可六丈，大而黄。六賊星，出正南，南方之星。去地可六丈，大而赤，數動，有光。司詭星，出正西，西方之星。去地可六丈，大而白，類太白。咸漢星，出正北，北方之星。去地可六丈，大而赤，數動，察之中青。此四星所出非其方，其下有兵，衝不利。”[102]顔師古引孟康曰：咸漢星“一名獄漢星”[103]。
《漢志》“司詭星”即《天官書》“司危星”，危、詭字同。《漢志》咸漢星即《天官書》獄漢星。孟康解《漢志》不言六賊星一名大賊星，顔師古亦不言，是兩人皆無此説。《晉書·天文中》叙“妖星”有此“四野星”[104]，其與《天官書》同作“司危”[105]，又與《漢志》同作“獄漢”，云“獄漢，一名咸漢”[106]，但“六賊”下不曰“一名大賊”，止曰“去地可六丈，大而赤，動有光”[107]，則《晉志》亦無此説。大賊星，史書不見有此稱。張守節《正義》“大賊星者，一名六賊”云云，乃承誤本强爲之説，故洪亮吉[108]、沈家本[109]兩人不信。
其本曰火。（4/1335/2）
《漢志》作“其本曰人”，孟康注：“星，石也。金石相生，人與星氣相應也。”則此是誤“人”爲“火”。（2/783/12-13）
按：考此《天官書》曰：“星者，金之散氣，其本曰火。星衆，國吉；少則凶。漢者，亦金之散氣，其本曰水。漢，星多，多水，少則旱，其大經也。”[110]火、水對舉，《史》文不誤，而是《漢志》文誤。張文虎曰：“疑《漢志》‘人’字即‘火’字壞文，孟康承誤本强爲之説。”[111]
姚範《援鶉堂筆記》載方東樹辨《漢志》“其本曰人”云：“下‘漢者，亦金散氣，其本曰水’，則此當從《史記》作‘火’。”[112]又辨孟康注“人與星氣相應”云：“人，字亦當作‘火’。如以金擊石取火矣。”[113]沈欽韓《漢書疏證》曰：“《史記》‘人’作‘火’。按：《淮南·天文篇》：‘天道曰圜，地道曰方。方者主幽，圜者主明。明者，吐氣者也，是故火曰外景；幽者，含氣者也，是故水曰内景。’蓋星爲陽精，爲外景，《史記》作‘火’爲是。”[114]今考《初學記》引《春秋説題辭》曰：“星之爲言精也，陽之榮也。”[115]陽之榮，亦當屬火。
星茀于河戍。（4/1349/2）
《漢志》作“河戍”，疑“戒”字之譌。南戒爲越門，北戒爲胡門也。（2/790/13）
按：梁氏所見本《史》文作“戒”字，文與今本相異，故有此論。
考此《天官書》曰：“越之亡，熒惑守斗；朝鮮之拔，星茀于河戍；兵征大宛，星茀招摇：此其犖犖大者。”[116]司馬貞《索隱》引《漢書·天文志》曰：“武帝元封之中，星孛于河戍，其占曰‘南戍爲越門，北戍爲胡門’。其後漢兵擊拔朝鮮，以爲樂浪、玄菟郡。”[117]小司馬又曰：“其河戍即南河、北河也。”[118]今本《史》文皆作“河戍”，則與《漢志》合。《史記會注考證》作“河戒”[119]，水澤利忠曰：“戒，慶、中統、彭：戍。”[120]
王念孫所見本《史》文作“河戒”，則是與梁氏所見本同。王念孫引王引之曰：“作‘戍’者是也。戍，讀戍申、戍甫之戍。《説文》：‘戍，守邊也。’戍訓守邊，故南戍爲越門，北戍爲胡門。《晉書》、《隋書》《天文志》並云：‘南河曰南戍，北河曰北戍。’《開元占經》南、北河戍字前後凡百餘見，皆作戍，不作戒，其《歲星》《熒惑》《太白》《辰星》四占並引《石氏》曰：‘守南河戍，蠻夷兵起，邊戍有憂。’《太白占》又引《甘氏》曰：‘太白守北河戍，邊戍有謀。’《流星占》引巫咸曰：‘流星犯南河，蠻夷兵起，防戍有憂。’《彗星占》引《海中占》曰：‘彗星犯南河，蠻越兵起，邊戍有憂。’然則河戍之戍，本作邊戍字明甚。上文‘鉞北，北河；南，南河’《正義》曰：‘南河三星，北河三星，分夾東井南北，置而爲戍。’今本《正義》戍作戒，後人所改也。戍，可言置；戒，不可言置。南河南戍，一曰陽門，亦曰越門；北河北戍，一曰陰門，亦曰胡門。置而爲戍者，謂置守邊之亭障也。故《開元占經·石氏中官占》引《黄帝占》曰：‘南、北河戍，一名天高，一名天亭。’義取戍邊之人，登亭障以侯望也。《唐書·天文志》曰：‘一行以爲，天下山河之象存乎兩戍。北戍，自三危、積石，負終南地絡之陰，東及大華、逾河，並雷首、厎柱、王屋、太行，北抵常山之右，乃東循塞垣，至濊貃、朝鮮，是謂北紀，所以限戎狄也。南戍，自岷山、嶓冢，負地絡之陽，東及太華、連商山、熊耳、外方、桐柏，自上洛南逾江、漢，攜武當、荆山，至于衡陽，乃東循嶺徼，達東甌、閩中，是謂南紀，所以限蠻夷也。故《星傳》謂北戍爲胡門，南戍爲越門。’一行所論正取邊戍之義，其字亦當作‘戍’。且一行開元中受詔治新曆，與司馬貞、張守節及作《開元占經》之瞿曇悉達皆同時人，斷無諸家‘河戍’字不誤，而一行獨誤作‘戒’之理。自傳寫者誤書作‘戒’，而文義遂不可通。淺人襲謬承譌，反以作‘戒’者爲正文，而改《史記》之‘河戍’以從之則惑矣。”[121]其説甚精，故全録如上，毋煩辭費。
封禪書第六
祠之萊山。皆在齊北。（4/1367/14）
《史詮》曰：“‘山’指之罘、之萊二山，故云‘皆’也。今本‘山’字屬上句，誤。”（2/801/6）
按：《史詮》讀“山皆在齊北”爲句，“山”字屬下，實誤。
《史》此處“山”字，即萊山；“皆”字，乃謂之罘、萊山。考此《封禪書》曰：“八神：一曰天主，祠天齊。天齊淵水，居臨菑南郊山下者。二曰地主，祠泰山梁父。蓋天好陰，祠之必於高山之下，小山之上，命曰‘畤’；地貴陽，祭之必於澤中圜丘云。三曰兵主，祠蚩尤。蚩尤在東平陸監鄉，齊之西境也。四曰陰主，祠三山。五曰陽主，祠之罘。六曰月主，祠之萊山。皆在齊北，並勃海。七曰日主，祠成山。成山斗入海，最居齊東北隅，以迎日出云。八曰四時主，祠琅邪。琅邪在齊東方，蓋歲之所始。皆各用一牢具祠，而巫祝所損益，珪幣雜異焉。”[122]裴駰《集解》引韋昭云：“（六曰月主，祠之萊山）在東萊長廣縣。”[123]此叙“八神”，曰“祠泰山梁父”、“祠三山”，曰“祠之罘”，曰“祠成山”，曰“祠琅邪”，各山名前皆無“之”字，則“祠之萊山”之“之”字恐是衍文。萊山，山名。《漢書·地理志上》曰：“（琅邪郡）長廣，有萊山萊王祠。”[124]此乃韋昭注所本。今考《漢書·郊祀志上》曰：“五曰陽主，祠之罘山；六曰月主，祠萊山：皆在齊北，並勃海。”[125]《史》《漢》相校，得失自見。《史》言“祠之萊山”，衍“之”字。
《通志·諸雜祠》叙“八神”有云：“五曰陽主，祠之罘山，在東莱；六曰月主，祠莱山，山在東莱長廣：皆在齊北，並勃海。”[126]《齊乘》引《史記·封禪書》云：“祠萊山，爲月主。”[127]皆作“祠莱山”。水澤利忠校《封禪書》云：“祠之萊山，景、蜀：無‘之’字。”[128]《封禪書》“六曰月主，祠之萊山”，郭嵩燾辨曰：“《漢志》琅邪長廣縣有萊山，此當云‘月主，祠萊山’。云‘祠之萊山’，承上‘祠之罘’而衍‘之’字。”[129]甚是。
《史詮》不知《史》文“祠之萊山”衍“之”字，故讀“祠之萊”爲句，將“之萊”作一山名解。中華書局修訂本《史》文將“萊山”作山名解，而不以“之萊”作山名，[130]甚是。
禹疏九江。（4/1391/1）
“江”乃“河”之誤，《漢志》是“九河”。（2/813/3）
按：《封禪書》作“九江”不誤，不必盡據《漢志》改。古書自有此叙事之法。
今考《史記·河渠書》曰：“禹疏九江。”[131]文與《封禪書》同。古書有作“三江”者，如《吕氏春秋·貴因篇》曰：“禹通三江。”[132]《淮南子·本經篇》曰：“舜乃使禹疏三江。”[133]又考《五帝本紀》曰：禹“决九河”[134]。則與《漢志》同。
江水分道，故謂之九江、三江。河水分道，故謂之九河。魏源曰：“九江猶九河。九河爲河水之自分爲九，則九江亦必一江自分爲九。”[135]姚鼐曰：“昔禹主名山川。九河自河分，故名曰河。三江、九江皆自江分，故名曰江。”[136]言九、三，乃極言河水、江水分道之多，寫河水、江水泛濫中國之狀，不可泥於其數而實求。《五帝本紀》曰：“禹之功爲大，披九山，通九澤，决九河。”[137]九，乃虚指可知。
大禹疏通九州水道，治水之泛濫，故《荀子·成相篇》曰：“禹北决九河，通十二渚，疏三江。”[138]《淮南子·泰族篇》曰：“禹鑿龍門，闢伊阙，决江濬河，東注之海。”[139]《要略篇》曰：“禹剔河而道九岐，鑿江而通九路。”[140]《後漢書·方術列傳上》曰：“昔大禹决江疏河，以利天下。”[141]
平準書第八
初先是往十餘歲河决觀，梁楚之地固已數困，而緣河之郡隄塞河，輒决壞，費不可勝計。（4/1424/12）
“初先是往”四字疊用，殊乖文義，當依《漢志》作“先是十餘歲”。（2/828/2）
按：初、先是、往，同義，此乃史公行文慣用繁重字之例。
劉淇《助字辨略》“先”字條嘗云：“《漢書·食貨志》：‘先是十餘歲河决灌，梁楚地固已數困。’先是，追原之辭也。《史記·平凖書》作：‘初先是往十餘歲河决觀，梁楚之地固已數困。’初先是者，重言也。往，亦先是之辭。此以四字爲重言者也。”[142]《史》文多重言，有重兩詞者，有重三詞者，亦有重四詞者。
重兩詞：例如《鄭世家》曰：“初往年鄭文公之卒也。”[143]既云“初”，又云“往年”；又如《陳杞世家》曰：“夏后禹之後苗裔也。”[144]既云“後”，又云“苗裔”。
重三詞：例如《平準書》此文之“初先是往”，既云“初”，又云“先是”，再云“往”；又如《項羽本紀》曰：“孤特獨立而欲常存。”[145]既云“孤”，又云“特”，再云“獨”，而《漢書·項籍傳》則作“孤立而欲長存”[146]，是《漢》減《史》“特”、“獨”兩字。
重四詞：例如《曹相國世家》曰：“（曹）參見人之有細過，專掩匿覆蓋之，府中無事。”[147]既云“掩”，又云“匿”，再云“覆”，後云“蓋”；又如《伯夷列傳》曰：“此其尤大彰明較著者也。”[148]既云“彰”，又云“明”，再云“較”，後云“著”。
【注释】
[1]趙生群師説：“《兵書》今題作《律書》。……今本《律書》凡二稱‘太史公曰’，全文言兵與言律兩部份涇渭分明，言律之文顯係後人割取《律曆書》的内容充數者。”（趙生群：《〈史記〉亡缺與續補考》，《太史公書研究》，第44頁）張大可説：“《律書》篇首之序乃《兵書》遺文，‘七正二十八舍’以下割取《律曆書》之文。……補亡者取成書補亡，……分《律曆書》以補《兵書》而更名《律書》。”（張大可：《〈史記〉殘缺與補竄考辨》，《史記研究》，第180—186頁）
[2]近年專門探討或涉及《史記·律書》“律數”内容的論文，包括劉文榮《律名與律數》（《大舞臺》2011年第3期）、譚映雪《〈史記·律書〉中“律數”與“生黄鐘術”》（《天津音樂學院學報》2010年第1期）、黄大同《千年聚訟的〈史記·律書〉律數考》（《文化藝術研究》2009年第6期）、劉文榮《〈史記·律書〉中的生律法研究》（《黄河之聲》2009年第7期）、關曉武《也論〈史記·律書〉中的律數》（《内蒙古師範大學學報》自然科學漢文版2007年第6期）、劉勇《漢代律學概覽》（《中國音樂學》2003年第1期）。今之學界雖對《史記·律書》“律數”多所討論，但仍難以取得一致的意見。
[3]〔漢〕司馬遷：《史記》卷二五，第1249—1250頁。
[4]〔宋〕蔡元定：《律吕新書》卷二，《文淵閣四庫全書》第212册，第22—23頁。
[5]〔宋〕蔡元定：《律吕新書》朱序，《文淵閣四庫全書》第212册，第4頁。
[6]〔清〕王元啓：《史記三書正譌》，《二十五史補編》第1册，第61頁。
[7]同上。
[8]［日］瀧川資言考證、水澤利忠校補：《史記會注考證附校補》卷二五，第715頁。(www.xing528.com)
[9]丘瓊蓀：《歷代樂志律志校釋》第1册，人民音樂出版社，1999年，第120頁。
[10]〔宋〕沈括撰、胡道静校證：《夢溪筆談校證》卷八，上海人民出版社，2011年，第258頁。
[11]〔清〕錢塘：《史記三書釋疑》卷一，《二十五史補編》第1册，第100頁。
[12]黄大同：《千年聚訟的〈史記·律書〉律數考》，《文化藝術研究》2009年第6期。
[13]蔡元定《律吕新書》“虚”條云：“黄鐘圍（面冪、底面積——引者注）有九方分（平方分——引者注）黄鐘爲龠（容積單位——引者注）爲八百一十分（立方分——引者注）。”（〔宋〕蔡元定：《律吕新書》卷二，《文淵閣四庫全書》第212册，第26頁）錢塘《史記三書釋疑》曰：“律體圓如柱體，積八百十分（立方分——引者注），則面冪（圍、底面積——引者注）必九分（平方分——引者注），以冪除積而得九寸之長。”（〔清〕錢塘：《史記三書釋疑》卷一，《二十五史補編》第1册，第100頁）《太平御覽》引《月令章句》曰：“黄鐘之管長九寸……圍九分（平方分——引者注）。其餘皆稍短，唯大小圍數無增減。”（〔宋〕李昉等：《太平御覽》卷一六，第82頁）
[14]〔漢〕班固：《漢書》卷二一上，第963頁。
[15]〔元〕劉瑾：《律吕成書》卷一，《文淵閣四庫全書》第212册，引用有删節，第141頁。
[16]〔元〕劉瑾：《律吕成書》卷一，《文淵閣四庫全書》第212册，第122頁。
[17]〔宋〕蔡元定：《律吕新書》卷一，《文淵閣四庫全書》第212册，第7頁。
[18]〔宋〕蔡元定：《律吕新書》卷二，《文淵閣四庫全書》第212册，第25頁。
[19]黄大同説：“在古代數學中，不論作爲面積平方數還是體積立方數的積數的表示，均爲長度單位形式。”（黄大同：《千年聚訟的〈史記·律書〉律數考》，《文化藝術研究》2009年第6期）
[20]〔漢〕班固：《漢書》卷二一上，引用有删節，第956—970頁。
[21]（南朝宋）范曄：《後漢書》志一，第2999頁。
[22]〔宋〕蔡元定：《律吕新書》卷二，《文淵閣四庫全書》第212册，第20頁。
[23]〔漢〕劉安撰、劉文典集解：《淮南鴻烈集解》卷三，馮逸、喬華點校，第135頁。
[24]〔漢〕班固：《漢書》卷二一上，第966頁。
[25]〔明〕朱載堉：《律吕正論》卷一，《續修四庫全書》第114册，第316—317頁。
[26]〔明〕朱載堉：《律吕正論》卷一，《續修四庫全書》第114册，第320頁。
[27]〔明〕朱載堉：《律吕正論》卷一，《續修四庫全書》第114册，第321頁。
[28]〔清〕江永：《律吕闡微》卷一，《文淵閣四庫全書》第220册，第556—557頁。
[29]〔戰國〕吕不韋撰、陳奇猷校注：《吕氏春秋新校釋》卷六，第328頁。
[30]〔漢〕劉安撰、劉文典集解：《淮南鴻烈集解》卷三，馮逸、喬華點校，引用有删節，第135—140頁。
[31]〔漢〕司馬遷：《史記》卷二六，第1260頁。
[32]〔漢〕司馬遷：《史記》卷二五，第1252頁。
[33]〔漢〕班固：《漢書》卷二一上，第958頁。
[34]〔梁〕沈約：《宋書》卷一一，第211—212頁。
[35]〔漢〕司馬遷：《史記》卷二五，第1251頁。
[36]［日］瀧川資言考證、水澤利忠校補：《史記會注考證附校補》卷二五，第716頁。
[37]譚映雪：《〈史記·律書〉中“律數”與“生黄鐘術”》，《天津音樂學院學報》2010年第1期；劉文榮：《〈史記·律書〉中的生律法研究》，《黄河之聲》2009年第7期；丘瓊蓀：《歷代樂志律志校釋》第1册，第119頁。
[38]〔漢〕劉安撰、劉文典集解：《淮南鴻烈集解》卷三，馮逸、喬華點校，第135頁。
[39]〔宋〕蔡元定：《律吕新書》卷二，《文淵閣四庫全書》第212册，第23頁。
[40]〔清〕王元啓：《史記三書正譌》，《二十五史補編》第1册，第62頁。
[41]〔漢〕班固：《漢書》卷二一上，第962頁。
[42]〔漢〕班固：《漢書》卷二一上，第963頁。
[43]〔漢〕司馬遷：《史記》卷二五，中華書局，2014年，第1490頁。
[44]〔漢〕司馬遷：《史記》卷二五，中華書局，2014年，第1497頁。
[45]同上。
[46]董樹巖、戴念祖、羅琳：《〈史記·律書〉律數匡正——兼論先秦管律》，《自然科學史研究》1994年第1期。
[47]黄大同：《千年聚訟的〈史記·律書〉律數考》，《文化藝術研究》2009年第6期。
[48]今據胡氏文之尾注知，此即戴念祖《〈史記·律書〉律數匡正——兼論先秦管律》一文。
[49]胡企平：《“黄鐘長八寸七分一”是先秦管律中完全正確的黄鐘宫音管長嗎？——與戴念祖先生〈先秦管律的可能性〉一文中所據以校改的觀點商榷》，《黄鐘》2012年第4期。
[50]同上。
[51]丘瓊蓀評論《隋志》引《史記·律書》作“七分”之時説：“是初唐時之《律書》已作‘七分一’，其誤已久。”（丘瓊蓀：《歷代樂志律志校釋》第1册，第123頁）
[52]〔南朝宋〕范曄：《後漢書》志一，第3001頁。
[53]〔漢〕司馬遷：《史記》卷二六，第1260頁。
[54]〔漢〕司馬遷：《史記》卷二六，第1261頁。
[55]同上。
[56]〔漢〕班固：《漢書》卷二一上，第975頁。
[57]〔漢〕班固：《漢書》卷二一上，第976頁。
[58]〔清〕方苞：《史記注補正》，《二十五史三編》第1册，第63頁。
[59]〔清〕王元啓：《史記三書正譌》，《二十五史補編》第1册，第68頁。
[60]〔清〕王念孫：《讀史記雜志》，《二十五史三編》第1册，第536—537頁。
[61]〔清〕梅文鼎：《曆學答問》，《叢書集成初編》第1325册，第7頁。
[62]〔清〕王玉樹：《經史雜記》卷七，《續修四庫全書》第1156册，第437頁。
[63]〔清〕王先謙：《漢書補注》，第400頁。
[64]〔清〕沈欽韓：《漢書疏證》卷一二，上海古籍出版社，2006年，第381頁。
[65]同上。
[66]〔漢〕司馬遷：《史記》卷二七，第1289頁。
[67]同上。
[68]〔清〕錢大昕：《廿二史考異》卷三，方詩銘、周殿傑校點，第39頁。
[69]〔清〕方苞：《史記注補正》，《二十五史三編》第1册，第66頁。
[70]〔漢〕司馬遷：《史記》卷六，第242頁。
[71]〔漢〕班固：《漢書》卷二六，第1274—1279頁。
[72]〔唐〕房玄齡等：《晉書》卷一一，中華書局，1974年，第289頁。
[73]〔唐〕魏徵、令狐德棻：《隋書》卷一九，中華書局，1973年，第529頁。
[74]王叔岷：《史記斠證》卷二七，第1091頁。
[75]李人鑒：《太史公書校讀記》，第335—337頁。
[76]〔漢〕司馬遷：《史記》卷二七，第1289—1308頁。
[77]〔漢〕司馬遷：《史記》卷二七，第1312頁。
[78]〔漢〕司馬遷：《史記》卷二七，第1318頁。
[79]〔漢〕司馬遷：《史記》卷二七，第1320頁。
[80]〔漢〕司馬遷：《史記》卷二七，第1325頁。
[81]〔漢〕司馬遷：《史記》卷二七，第1328頁。
[82]〔清〕王念孫：《讀史記雜志》，《二十五史三編》第1册，第539頁。
[83]〔唐〕魏徵、令狐德棻：《隋書》卷二一，第607頁。
[84]〔漢〕班固：《漢書》卷二六，第1285頁。
[85]〔唐〕房玄齡等：《晉書》卷一二，第319頁。
[86]〔漢〕司馬遷：《史記》卷二七，中華書局，2014年，第1574頁。
[87]〔漢〕司馬遷：《史記》卷二七，第1320頁。
[88]〔漢〕司馬遷：《史記》卷二七，第1321頁。
[89]〔清〕王念孫：《讀史記雜志》，《二十五史三編》第1册，第539頁。
[90]［日］瀧川資言考證、水澤利忠校補：《史記會注考證附校補》卷二七，第751頁。
[91]〔清〕王引之撰、孫經世補：《經傳釋詞附補及再補》卷七，第156頁。
[92]〔漢〕司馬遷：《史記》卷三二，第1512頁。
[93]［日］瀧川資言考證、水澤利忠校補：《史記會注考證附校補》卷三二，第878頁。
[94]王叔岷：《史記斠證》卷三二，第1328頁。
[95]蕭旭：《古書虚詞旁釋》卷二，廣陵書社，2007年，第44頁。
[96]〔漢〕司馬遷：《史記》卷二七，第1333—1334頁。
[97]〔漢〕司馬遷：《史記》卷二七，第1334頁。
[98]同上。
[99]〔清〕錢大昕：《廿二史考異》卷三，方詩銘、周殿傑校點，第29頁。
[100]李人鑒：《太史公書校讀記》，第371頁。
[101]〔漢〕司馬遷：《史記》卷二七，第1333—1334頁。
[102]〔漢〕班固：《漢書》卷二六，第1291—1292頁。
[103]〔漢〕班固：《漢書》卷二六，第1292頁。
[104]〔唐〕房玄齡等：《晉書》卷一二，第324—325頁。
[105]〔唐〕房玄齡等：《晉書》卷一二，第324頁。
[106]〔唐〕房玄齡等：《晉書》卷一二，第325頁。
[107]同上。
[108]〔清〕洪亮吉：《四史發伏》卷一，《四庫未收書輯刊》肆輯第20册，第74頁。
[109]〔清〕沈家本：《史記瑣言》，《二十四史訂補》第1册，第344頁。
[110]〔漢〕司馬遷：《史記》卷二七，第1335頁。
[111]〔清〕張文虎：《校刊史記集解索隱正義札記》，《二十四史訂補》第1册，第135頁。
[112]〔清〕姚範：《援鶉堂筆記》卷二一，《續修四庫全書》第1148册，第597頁。
[113]同上。
[114]〔清〕沈欽韓：《漢書疏證》卷二〇，第580頁。
[115]〔唐〕徐堅等：《初學記》卷一，第11頁。
[116]〔漢〕司馬遷：《史記》卷二七，第1349頁。
[117]〔漢〕司馬遷：《史記》卷二七，第1349頁。
[118]同上。
[119]［日］瀧川資言考證、水澤利忠校補：《史記會注考證附校補》卷二七，第762頁。
[120]［日］瀧川資言考證、水澤利忠校補：《史記會注考證附校補》卷二七，第780頁。
[121]〔清〕王念孫：《讀史記雜志》，《二十五史三編》第1册，第542—543頁。
[122]〔漢〕司馬遷：《史記》卷二八，第1367頁。
[123]〔漢〕司馬遷：《史記》卷二八，第1368頁。
[124]〔漢〕班固：《漢書》卷二八上，第1586頁。
[125]〔漢〕班固：《漢書》卷二五上，第1202頁。
[126]〔宋〕鄭樵：《通志》卷四三，中華書局，1987年，第583頁。
[127]〔元〕于欽：《齊乘》卷一，《宋元方志叢刊》第1册，中華書局，1990年，第523頁。
[128]［日］瀧川資言考證、水澤利忠校補：《史記會注考證附校補》卷二八，第807頁。
[129]〔清〕郭嵩燾：《史記札記》卷三，第142頁。
[130]〔漢〕司馬遷：《史記》卷二八，中華書局，2014年，第1645頁。
[131]〔漢〕司馬遷：《史記》卷二九，第1415頁。
[132]〔戰國〕吕不韋撰、陳奇猷校注：《吕氏春秋新校釋》卷一五，第933頁。
[133]〔漢〕劉安撰、劉文典集解：《淮南鴻烈集解》卷八，馮逸、喬華點校，第307頁。
[134]〔漢〕司馬遷：《史記》卷一，第43頁。
[135]〔清〕魏源：《書古微》卷五，《續修四庫全書》第48册，第540頁。
[136]〔清〕姚鼐：《惜抱軒九經説》卷三，《續修四庫全書》第172册，第619頁。
[137]〔漢〕司馬遷：《史記》卷一，第43頁。
[138]〔戰國〕荀况撰、王天海校釋：《荀子校釋》卷一八，上海古籍出版社，2005年，第990頁。
[139]〔漢〕劉安撰、劉文典集解：《淮南鴻烈集解》卷二〇，馮逸、喬華點校，第815頁。
[140]〔漢〕劉安撰、劉文典集解：《淮南鴻烈集解》卷二一，馮逸、喬華點校，第863頁。
[141]〔南朝宋〕范曄：《後漢書》卷八二上，第2710頁。
[142]〔清〕劉淇：《助字辨略》卷二，中華書局，2004年，第67頁。
[143]〔漢〕司馬遷：《史記》卷四二，第1767頁。
[144]〔漢〕司馬遷：《史記》卷三六，第1583頁。
[145]〔漢〕司馬遷：《史記》卷七，第308頁。
[146]〔漢〕班固：《漢書》卷四三，第1805頁。
[147]〔漢〕司馬遷：《史記》卷五四，第2030頁。
[148]〔漢〕司馬遷：《史記》卷六一，第2125頁。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
