(一)不同型号泵并联运行的边界条件
工程上经常将两台或多台水泵向同一管道供水,水泵的这种运行条件叫做水泵的并联运行。计算并联水泵的事故停泵水锤,可采用与单泵相同的方法确定其边界条件。由于每条并联管道都有一个水头平衡方程,每一台泵停止运行后又都有一个惯性方程,因此,并联水泵的台数及其中事故停泵的台数就确定了未知量的个数,同时也确定了边界方程的个数。
对于两种不同型号大小泵并联的情况,如图3-10所示,水泵端的边界条件方程由并联各泵的水头平衡方程、惯性方程、连续方程以及并联管道的特征方程组成。
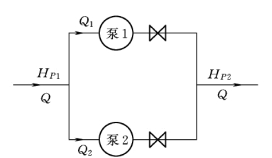
图3-10 并联水泵布置示意图
1.水泵工作状态方程


式中α1、α2、α3、α4 分别为扬程和转矩直线方程中的常数项。带脚标P 的为计算时段末各参数值。
2.水头平衡方程
1 号、2号泵的水头平衡方程如下:

式中 H1、H2——分别表示并联的1 号、2号泵的工作扬程;
HP1——管路并联处水头;
HS——进水池水位在基准面以上高度;ΔHv1、ΔHv2——分别表示1 号、2号蝶阀水头损失。

式中 Cv1、Cv2——分别表示阀门的水头损失系数;
QR1、QR2——分别表示1 号、2号泵额定流量。
3.相连管道的负特征方程
![]()
4.水流连续方程
由于连续性原理,并用无量纲流速v 表示水泵的瞬态流量,可得
![]()
由于水泵的瞬态扬程H=HRh,即等于无量纲扬程与水泵额定扬程的乘积,故采用全特性曲线表示时,水泵的瞬态工作扬程可分别由式(3-75)表示:
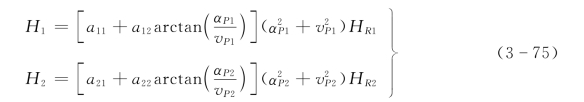
将式(3-72)、式(3-73)、式(3-74)、式(3-75)代入式(3-71),可以得到由水泵瞬态无量纲流量v 和无量纲转速α表示的各水泵水头平衡方程,为便于计算分别用F1、F2 表示为
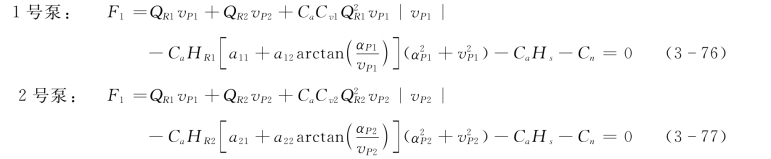
式中 a11、a12——表示1 号泵扬程直线方程中常数;
a21、a22——表示2号泵扬程直线方程中常数;
αP1、vP1——分别为1 号泵转速和流量相对值;
αP2、vP2——分别为2号泵转速和流量相对值。
式(3-76)、式(3-77)是一组f(α,v)=0非线性方程组,即相对转速和流量的方程组。
5.水泵机组的惯性方程
水泵机组转动部分在动力中断后,由于惯性的作用而继续旋转,其转矩M 与转速n的变化特性用惯性方程表示为

取微小的时间间隔积分,并引入无量纲转矩β(β=M/MR,MR 为额定转矩M)和无量纲转速α,可以得到以下形式的有限差分方程:
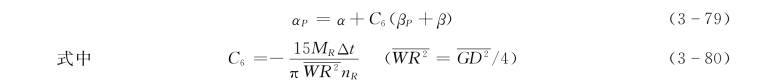
将全特性方程曲线转矩关系表达式(3-69)、式(3-70)代入式(3-79),可分别写出1 号、2号泵的惯性方程式,为便于数值计算,分别用F3、F4 表示:
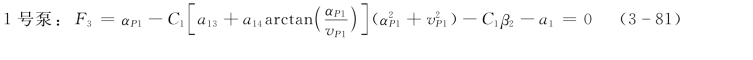
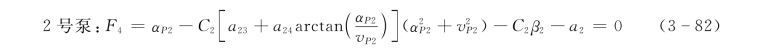
式中 a13、a14——为1 号泵转矩直线方程中常数项;
a23、a24——为2号泵转矩直线方程中常数项;带脚标P 的为时段末各参数值。(https://www.xing528.com)
式(3-81)、式(3-82)为用水无量纲流量v 和无量纲转速α表示的惯性方程。
6.并联边界条件方程求解
对于两种不同型号水泵并联的情况,当两台机组同时事故断电停泵,泵端边界条件方程由式(3-76)、式(3-77)、式(3-81)、式(3-82)4个方程组成,4个方程包含有4个未知量αP1、vP1、αP2、vP2,可以有唯一确定的解。由于方程组是一组非线性方程,可用牛顿—莱福笙迭代法求解。将上述4个方程写成以下迭代求解的矩阵形式:
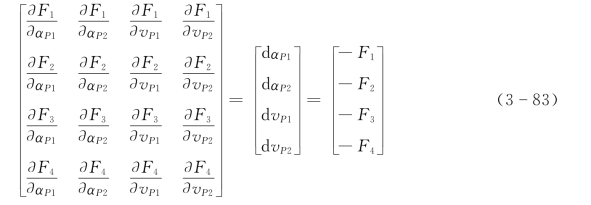
其中:

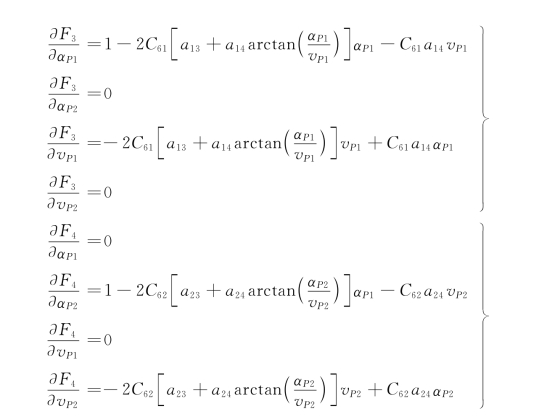
式(3-83)中包含有4个未知迭代增量dαP1、dαP2、dvP1、dvP2,可计算确定并逐步迭代求得各泵的瞬态流量和瞬态转速,其求解步骤如下所示:
(1)设定初值dαP1、dαP2、dvP1、dvP2,除稳态开始的第一时段外,其余时间段可用前一时段的值加上该时段的增值作为下一段的初值。
(2)计算方程中的常数项。

(6)将设定瞬态参量与求得的各瞬态增量相加求其代数和,得到更逼近于方程解的各瞬态参量,转向(3)开始重新迭代计算,直到|dαP1|≤ε、|dαP2|≤ε、|dvP1|≤ε、|dvP2|≤ε(ε为允许的计算误差),这时所求的dαP1、dαP2、dvP1、dvP2即为满足一定要求的精确解。
(二)串联水泵的边界条件
水泵的串联工作有两种情况:一是如果串联水泵中,水泵与水泵之间的连接管道很长,则每台泵都是一个独立的边界条件,可采用与单泵相同的方法处理,在此不再赘述;二是如果两个水泵之间管道很短,计算中可以将两个水泵之间管道略而不计,如图3-11所示。这时可按下述方法建立其边界条件方程。
1.水泵扬程方程
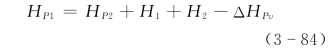
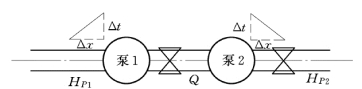
图3-11 串联水泵布置示意图
式中 HP1、HP2——分别表示水泵进、出口的压力水头;
H1、H2——分别表示水泵1 和水泵2的扬程;
ΔHPv——表示通过水泵和阀门的水头损失。
2.连续方程
由连续性原理可知
![]()
3.正特征线方程
水泵入口的正特征线方程:
![]()
4.负特征线方程
水泵出口的负特征线方程:
![]()
5.阀门水头损失方程
![]()
式中 Cv——表示阀门的损失系数。
6.通过水泵特性曲线建立方程
从水泵特性曲线中,建立如下4个方程
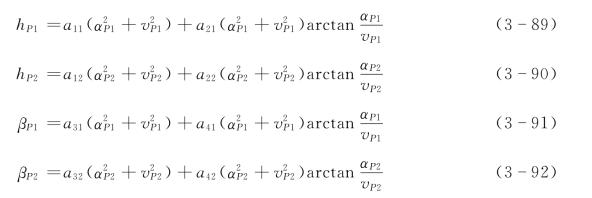
7.转动力矩方程
![]()
以上共有13 个方程,求解13 个未知量。经过计算简化可得以下3 个方程:
式(3-95)、式(3-96)、式(3-97)3 个方程,包含3 个未知数αP2、vP2和αP1,方程独立、封闭,可以求解。求解时先将F1、F2、F33 个方程线性化;然后用高斯消去法求增量ΔαP2、ΔvP2和ΔαP1;多次迭代后,当增量小于某一允许误差值,再进行下一时间步长的计算,直至计算到需要时刻或恒定流为止。
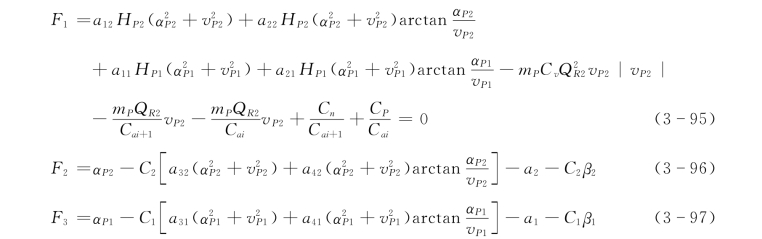
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




