新技术：单泵边界条件求解

为了确定水泵端在事故断电后不同时刻的Q、H 值，必须求出它们之间的关系，以便和水锤负特征线方程联立求解，但水泵的Q、H 值又和其转速n、转矩M 有关。因此，还必须根据水泵的全面特性曲线和机组惯性方程求出它们之间的关系，然后进行求解。

（1）水泵全特性曲线及其方程式。

水泵的Q、H、n和M 之间的关系可用全特性曲线θ—h/（α2＋v2）和θ—m/（α2 ＋v2）表示，如图3-8所示，图中：

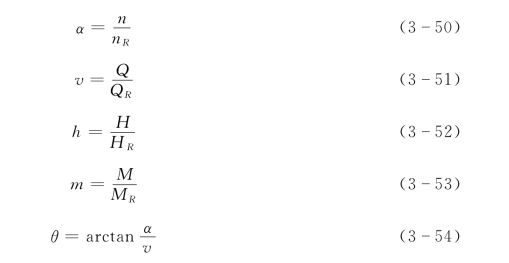
以上各式中，下标R 表示水泵的额定工况。

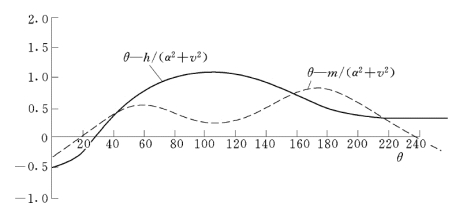
图3-8　泵全面特性曲线图

为了便于求解，等分θ＝0 到θ＝360°间的曲线，如果等分距Δθ足够小（例如Δθ＝5°），则两点间的曲线就可近似地视为直线，整个曲线就可用一段直线所取代，该直线方程为

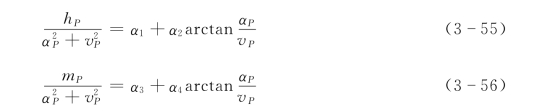
式中　α1、α2、α3、α4 分别为扬程和转矩特性直线方程中的常数，对不同线段其值不同，下标P 表示所求的未知数值。

（2）水泵机组惯性方程。

机组断电后，无外加转矩，所以减速转矩为

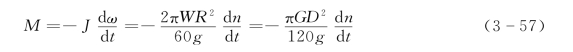
式中　　　　J——转动系统的惯性矩；

ω——角速度；

WR2、GD2——水泵机组的转动惯量；（GD2 的单位是kg·m2）；

其余符号意义同前。

将n和M 均用相对值α 和m 代替，同时m 值采用所历时段Δt 的平均值，则式（3-57）可改成有限差微分形式，即

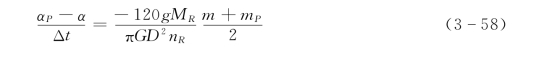
简写上式得

(www.xing528.com)

而

式中有下标P 的表示Δt 时段末的未知值，不带下标者为前一段的已知值。GD2 的单位是kg·m2。

式（3-58）中的GD2 如果用WR2 表示，则式（3-60）中的C6 值变为

但应用式（3-61）应注意，其中额定转矩MR 的单位为N·m。

（3）水泵出口处特性方程式。

水泵出口处特性方程为负水锤特征方程，即

式中符号意义同前。

联立式（3-45）、式（3-46）、式（3-61）和式（3-62）四个方程，经过代换可消去两个未知数，再经整理后，可得出泵出口管路无闸阀（或闸阀全开）和无逆止阀时事故断电情况下的下列两个方程式（以下水面为基线）

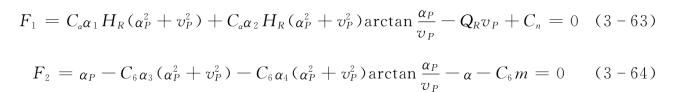
联立以上两式，即可求出αP、HP 值。对式（3-63）、式（3-64）可采用迭代法求解。即先假定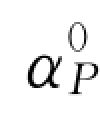 、 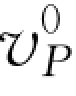为近似解，则其精确解为

式中　dαP、dvP 可用多元的泰勒级数展开，并取其线形项求得，即

如此反复迭代，直至其误差值dαP、dvP 小于规定值为止。

求出αP、vP 值后，即可求出其相应时段末的泵出口处的n、HP、QP 值，进而根据正、负特征线方程式求出管路中其他断面的流量和水头值。

计算步骤和计算机程序框图如图3-9 所示。

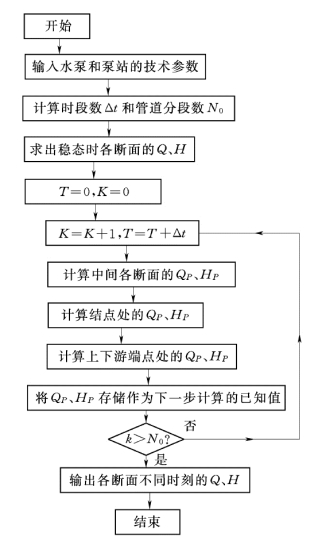
图3-9　水力过渡过程计算程序框图