解线性规划单纯型法与分枝定界法：理论与实践

1.单纯型法功能

用于求解线性规划问题。

2.目标函数

满足约束方程：

并要求

3.方法摘要

首先通过引入剩余变量、松弛变量，把式（2-5）的不等式约束方程组转换成等式方程组。它们的引入，不改变原问题的性质，故在目标函数中相应项的系数为0。

为了构造安全的单位矩阵，作为初始基变量，对原“≥”、“＝”形式的约束方程还需引入人工变量。这时，只有当人工变量为零时，才能得到式（2-5）的解。故目标函数中，相应项的系数应取一任意大正数M。如果am＋1，j≥0，j＝1，2，…，n，且人工变量为零，则基本可行解为最优解；若am＋1，j≥0，但有某个人工变量xL≠0，则该问题无可行解；若有某个am＋1，j＜0，则当xj 由零上升时，可使目标函数值增大，我们可使该变量进入基底，成为可行解的一个分量，称为基变量。通常取满足于am＋1，L ＝min（am＋1，j|1 ≤j≤n，am＋1，j ＜0）的足标L，以xL 作为基变量，若这样的L 不止一个，取足标最小者。换入基变量的增大，受到诸约束条件的限制。

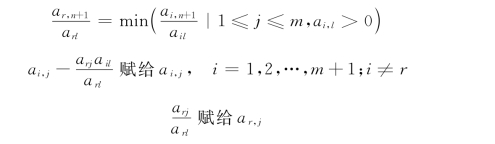
为使约束不遭受破坏，取满足的分量xr 作为换入基变量，若这样的r 不止一个，取足标最小者。这时新的基变量值依次为a1，n＋1，a2，n＋1，…，am，n＋1，目标函数s ＝am＋1，n＋1 在迭代过程中，若ai，j ≤0，i ＝1，2，…，m，则原问题有无界解，即目标函数值无上界。

单纯形求解流程图如图2-3 所示。

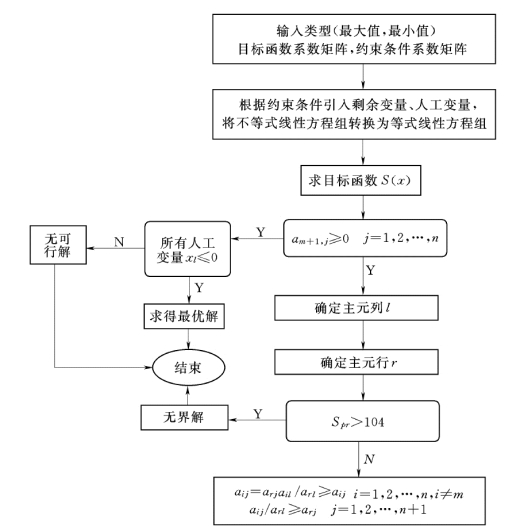
图2-3　单纯形求解流程图

4.整数规划法的分枝定界法

分枝定界法是一种隐枚举法或部分枚举法，它不是一种有效算法，是枚举基础上的改进，分枝定界法的关键是分枝和定界。

若整数规划的松弛问题的最优解不符合整数要求，假设xi＝bi 不符合整数要求，［bi］是不超过bi 的最大整数，则构成两个约束条件，xi ≤［bi］和xi ≥［bi］＋1。分别将其加入松弛问题中，从而形成两个分枝，即两个后继问题。两个问题的可行域中包含原整数规划问题的所有可行解。而在原松弛问题的可行域中，满足［bi］＜xi＜［bi］＋1的一部分区域在以后的求解过程中被遗弃了，然而，它并不包含整数规划的任何可行解。根据需要，各后继问题可以类似地产生自己的分枝，即自己的后继问题。如此不断继续，直到获得整数规划的最优解，这就是所谓的“分枝”。

所谓“定界”，是在分枝过程中，若某个后继问题恰巧获得整数规划的一个可行解，那么，它的目标函数值就是一个“界限”，作为处理其他分枝的一个依据。因为整数规划问题的可行解集是它的松弛问题可行解集的一个子枝，前者解的目标函数值不会优于后者函数值，所以，对于那些相应松弛问题最优解的目标函数值比上述“界限”值差的后继问题，就可以剔除而不再考虑了。当然，如果在以后的分枝过程中出现了更好的“界限”，而“定界”则可以取代原来的界限，这样可以提高定界的效果。

“分枝”为整数规划最优解的出现创造了条件，而“定界”则可以提高搜索的效率。经验表明：在可能的情况下，根据对实际问题的了解，选择一个合理的“界限”，可以提高分枝定界法的搜索效率。(www.xing528.com)

分枝定界法解整数规划的一般步骤如下：

步骤1：称整数规划问题为问题A，它的松弛问题为问题B，以zb 表示问题A的目标函数的初始界（如已知问题A的一个可行解，则它的目标函数值为zb）。对最大化问题A，zb 为下界；对最小化问题A，zb 为上界。解问题B，转步骤2。

步骤2：如问题B无可行解，则问题A也无可行解；如问题B的最优解符合问题A的整数要求，则它就是问题A的最优解。对于这两种情况，求解过程到此结束。如问题B的最优解存在，但不符合问题A的整数要求，则转步骤3。

转步骤3：对问题B，任选一个不符合整数要求的变量进行分枝。设选择xj＝bj，且设［bj］为不超过bj 的最大整数。对问题B分别增加下面两个约束条件中的一个：

从而形成两个后继问题，转步骤4。

步骤4：考查所有后继问题，如其中有某几个存在最优解，且最优解符合问题A的整数要求，则以它们中最优的目标函数值和界zb 比较，若比界zb 更优，则以其取代原来的界zb，并称相应的问题为问题C。否则，原来的界zb 不变，转步骤5。

转步骤5：不属于C的后继问题中，存在最优解，且其目标函数值比界zb 更优的后继问题为待检查的后继问题。

若不存在待检查的后继问题，当问题C存在时，问题C的最优解就是问题A的最优解；当问题C不存在时，和界zb 对应的可行解就是问题A的最优解。zb 即为问题A的最优解的目标函数值，求解到此结束。

若存在待检查的后继问题，则选择其中目标函数值最优的一个后继问题，改称其为问题B，回到步骤3。

分枝定界法计算机求解数学模型如下：

目标函数：

满足约束方程：

并要求

分枝定界法的程序框图如图2-4所示。

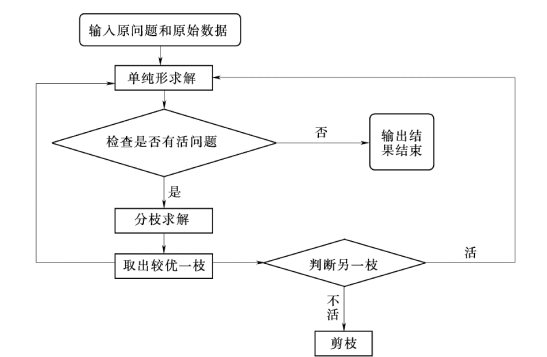
图2-4　分枝定界法的程序框图