振动孔隙水压力的增长模型是土动力研究中的重要课题,也是土体有效应力动力分析的基础。自从汪闻韶1962年提出第一个模型以来,国内外学者提出了很多振动孔隙水压力的增长模型。按其与孔压相联系的主要特征,大致可分为应力模型、应变模型、能量模型、内时模型、有效应力路径模型和瞬时模型[149]。试验结果表明,振动孔隙水压力的模型应该可以考虑以下三个基本因素:
(1)土的性质。孔隙水压力的增长模型是一个很复杂的课题,还缺少适宜各类不同土性的普遍理论解答。因此,根据所研究课题,通过室内试验确定孔隙水压力的增长模型仍然是一种最有效的方法。
(2)振前应力状态。主要用初始平均有效应力σ′m0和静应力水平sl表示。σ′m0是通过土的密度来影响振动孔隙水压力发展的,σ′m0愈大,土愈密,孔隙水压力发展愈慢。sl表示振前土体已经承受的剪切程度,sl较大的土由于振前已经发生较大的剪切变形,孔隙水压力的增长较慢,最终累计值也较小。
(3)动荷载的特点。动荷载是孔隙水压力产生的外因,显然,动应力的幅值愈大,循环的次数愈多,积累的孔隙水压力也愈高。而频率的影响不大,一般可忽略。
1.上海地区黏性土的孔隙水压力增长模型
根据现有资料,上海地区黏性土的振动孔隙水压力u*的增长模型可以采用以下经验公式:
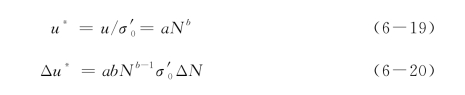
式中:σ′0为初始平均有效应力;N是累计振动次数;a,b是试验参数,可参考表6-2取值[73]。
表6-2 上海地区黏性土的a、b试验参数
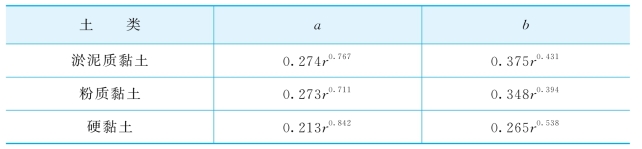
表中,r为循环压力比,即动剪应力τd与初始平均有效应力σ′0的比值。
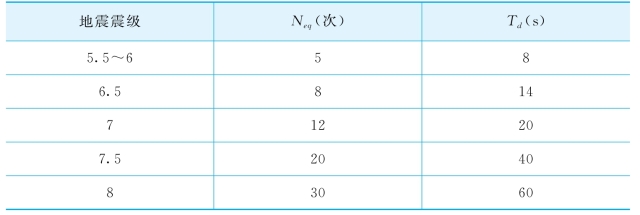
在地震反应计算中,每一时段的等效振动次数ΔN可按下述方法近似确定。首先根据Martin等1979年的研究,从表6-3中查出不同震级地震的持续时间T d和等效振动次数N eq。然后计算时间间隔ΔTi=ti-ti-1内的地震波能量与整个持续时间T d内的地震波能量之比:
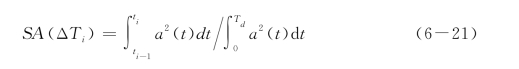
再按下式计算ΔN:
![]()
式(6-22)的物理意义是以时段ΔT i内地震波能量的相对大小为权系数,将总的等效振动次数N eq按权系数的大小分配到各时段内。
表6-3 Neq与T d的经验取值
2.上海地区砂性土的孔隙水压力增长模型
上海地区砂性土的振动孔隙水压力比u*的增长模型可以采用以下公式[73](https://www.xing528.com)
![]()
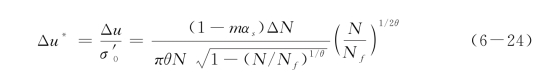
式中:Δu——在ΔT时间内由于地震振动而产生的孔隙水应力;
5σ′0——初始平均有效应力;
5m——试验参数,一般取1.0~1.2;
5αs——静应力水平,即τs/σ′0,按式(6-26)求解;
5ΔN——每一时段的等效振动次数,按式(6-22)求解;
5N——累计振动次数,N=∑ΔN;
5θ——常数,Seed认为对于大多数土可取0.7;
5N f——无初始水平剪应力情况下达到破坏所需要的振动次数,也
即达到液化(u*=1)所需的振动次数,按式(6-25)求解。
现有研究表明,液化振动次数N f与动剪应力比τd/σ′0存在下述平均关系[150,152]:
![]()
式中,τd为破坏面上的循环剪应力幅值,a和b为试验常数。
在平面应变状态下,假定最大往返剪切作用面为破坏面,那么破坏面上的初始静剪力比αs和动剪应力比αd分别为[153-154]:
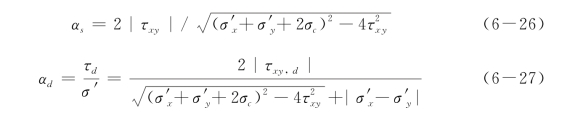
式中,σ′x、σy′和τxy分别为土单元的静有效正应力和水平面上的静剪应力;σc=c′·ctgφ′,c′和φ′分别为土的有效粘聚力和内摩擦角,对于纯净砂土,c′=0;τxy,d为水平面上地震剪应力的等效循环幅值。对于水平场地,τxy=0,因此,αs=0;αd=|τxy,d|/(σ′y+σc),这里已假定σ′y>σ′x;若场地土为纯净砂土,σc=0,则αd=|τxy,d|/σ′y,即αd为水平面上的地震剪应力和竖向有效应力之比。
上海地区的N f也可参考下式确定[155]:

式中,Rf是动强度;qcyc,pc分别是动三轴试验的循环应力和平均正应力。土的动强度采用破坏应变标准。在等压固结条件下,N f取双幅应变达到5%的振动周数。在偏压固结条件下,N f取总应变幅达到5%的振动周数。m,n是试验参数,对于砂性土分别等于0.71和-0.059,对于黏性土分别等于0.533和-0.058。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




