土性对结构地基动力相互作用的影响

在前面介绍的上海地区实际土层的基础上，假设土层的动剪切模量为G，将土体的动剪切模量分别乘以0.1、0.5、1、2、5、10倍(下文分别记为0.1G、0.5G、1G、2G、5G和10G)，进行了考虑结构-地基动力相互作用的三维有限元计算分析，探讨了土性的不同对相互作用效果的影响。

1.不同土性时体系的自振频率

不同土性下结构-地基相互作用体系的前10阶自振频率如表5-20所示。从表中可看出，随着土体动剪切模量的增大，相互作用体系的自振频率不断增大，而且高阶频率的增大幅度明显大于低阶频率的增长。结构-地基相互作用体系的频率低于刚性地基上结构的自振频率，也就是考虑动力相互作用后，结构的自振频率降低，自振周期延长。这与以前众多学者的研究成果一致[7，8，71，84，146]。

2.不同土性时结构的加速度及位移反应

按第2.9节中图2-20和式(2-1)对本节相互作用体系的结构顶层位移反应组成进行分析，如表5-21所示。表中，u为结构顶层总位移，Hθ为基础转动引起的摆动位移，u g为基础平动引起的平动位移，ue为上部框架结构的弹性变形。

表5-20　不同土性时相互作用体系的自振频率比较

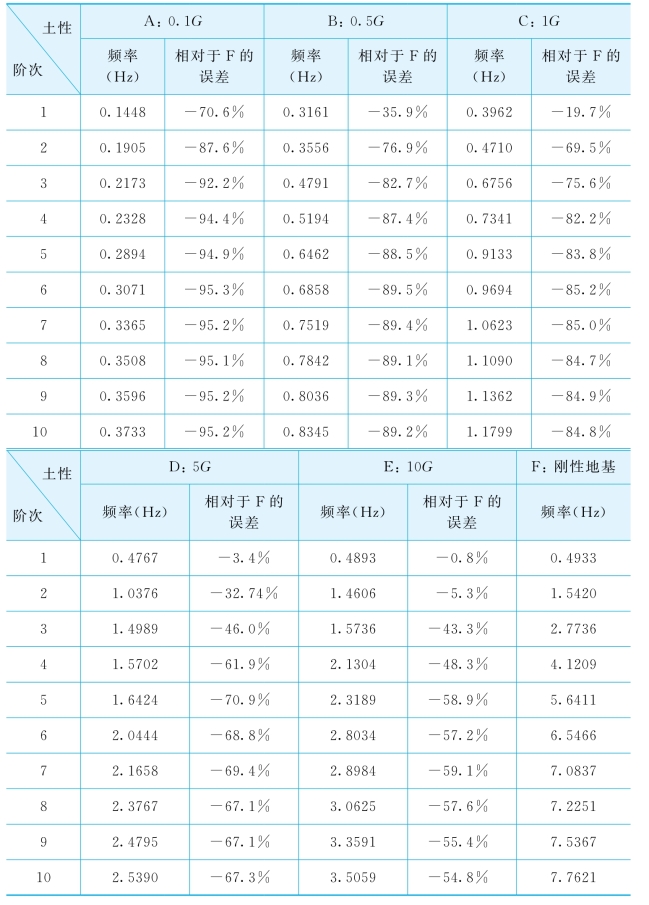
图5-24和图5-25分别给出了不同土性时结构的加速度反应峰值和位移反应峰值。从图5-24可看出，相对于土体底部输入的地震波加速度峰值0.1 g而言，土性0.1G、0.5G和1G情况下基底的加速度峰值均小于0.1 g，软土表现出明显的隔震作用；土性2G、5G和10G情况下，基底加速度峰值大于0.1 g，土体对地震动起放大作用；且结构加速度反应随土的动剪切模量的增加，整体上呈增大的趋势。

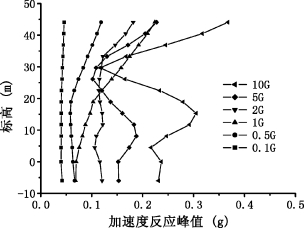
图5-24　不同土性时结构加速度反应峰值

图5-25　不同土性时结构位移反应峰值(www.xing528.com)

表5-21　不同土性时结构顶层位移组成分析(单位：m)

从图5-25和表5-21可看出，土性为0.1G、0.5G和1G时，随着土体剪切模量增加，结构的位移反应峰值增大，这主要是因为这三种情况下摆动分量和平动分量基本相当，而弹性变形分量随土体硬度增加而增加所致。土性2G、5G和10G情况下，由于土体刚度较大，相对于土性1G而言，摆动分量和平动分量较小，致使土性2G、5G和10G情况下的位移反应较土性1G情况下小。在土性2G、5G和10G情况下，随土体剪切模量增加，结构的位移反应峰值减小，这是因为这三种情况下的平动分量和弹性变形分量相当，而摆动分量随土体刚度增加而减小所致。

通过对不同土性时相互作用体系的自振频率进行分析发现，土性0.1G和0.5G时，在振动方向上一阶振型的参与最为显著；而随着土体动剪切模量的增加、土体变硬，在振动方向上二阶振型占据主导地位，且结构的弹性变形所占比重逐渐增大，因此随着土体动剪切模量的增大，结构的加速度和位移反应峰值分布曲线形状变得较为复杂。

3.不同土性时结构的层间剪力及倾覆力矩反应

图5-26和图5-27分别给出了不同土性时结构的最大层间剪力和最大倾覆力矩分布。可看出，土性0.1G、0.5G和1G情况下，结构最大层间剪力及最大倾覆力矩随土体动剪切模量的增大而增大；土性2G、5G和10G情况下，结构最大层间剪力及最大倾覆力矩也随土体动剪切模量的增大而增大。但2G和5G时的最大层间剪力及最大倾覆力矩均小于1G时的相应值，这主要因为结构的最大层间剪力和倾覆力矩与结构的加速度反应相关，因而变得较为复杂，并不是随着土体动剪切模量的增大一直增大。

图5-26　不同土性时结构最大层间剪力

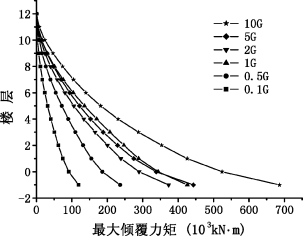
图5-27　不同土性时结构最大倾覆力矩

4.不同土性时土体的加速度反应

在土体的水平中心处、沿深度方向取20个点，当土体底部输入加速度峰值0.1 g的地震波、土性不同时分别输出它们的加速度时程计算结果。由计算得出20个点的加速度峰值，绘出不同土性时不同高度处土体的加速度峰值与各点标高的关系曲线如图5-28所示。由图中可以看出，土性0.1G和0.5G时，软土起隔震效果，土体的加速度峰值均小于0.1 g；土性1G时，靠近底部的土体动剪切模量较大，对输入的地震动起放大作用，加速度峰值大于0.1 g，而上部土体较软起隔震作用，加速度峰值小于0.1 g；土性2G、5G和10G时，土体较硬对地震动起放大作用，土表加速度峰值均大于0.1 g。软土对地震动起隔震作用，较硬土体对地震动的放大作用与许多学者的研究成果一致[9，136]。