为了研究不同上部结构形式对相互作用效果的影响,本节进行了某框剪结构与土体的动力相互作用计算分析,并与前面的框架结构做了对比。为了使计算结果具有可比较性,此框剪结构体系是在前面框架结构体系的基础上,保持其他参数不变,仅增加四片“L”形剪力墙构成,剪力墙厚度为200 mm,混凝土采用C30强度等级,结构平面布置如图5-10所示。
在进行该框剪结构相互作用体系的计算建模时,剪力墙采用SHELL单元模拟,其余部分的单元选取与网格划分、土体模型的选取、阻尼模型的选取、人工边界的施加都与框架结构相互作用体系建模时相一致。
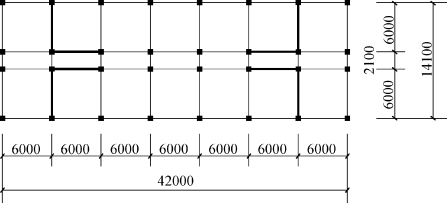
图5-10 框剪结构平面布置
1.不同上部结构形式时体系的自振频率
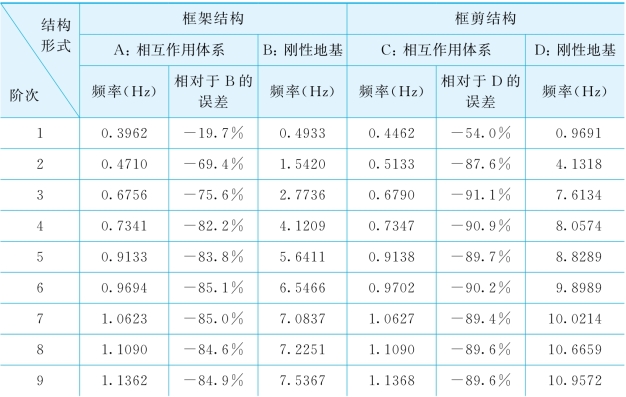
表5-12给出了不同上部结构形式时相互作用体系自振频率比较,从表中A和C列的比较可看出,框剪结构相互作用体系的频率要比框架结构相互作用体系的频率高。从表中还可看出,考虑土-结构动力相互作用后,两种体系的频率都比刚性地基时有大幅度的降低,且框剪结构体系频率的降低程度要比框架结构的显著得多。
表5-12 不同上部结构形式时相互作用体系的自振频率比较
![]()
2.不同上部结构形式时结构的加速度及位移反应
对不同上部结构形式下考虑结构-地基动力相互作用的结构动力反应计算结果进行分析,结构的加速度反应峰值和位移反应峰值分别如图5-11和图5-12所示。从图中可以看出,框剪结构的加速度反应和位移反应均比框架结构的反应要小。这可能是因为框架结构的自振频率与土体的自振频率更加接近,造成了土体与上部结构的共振。
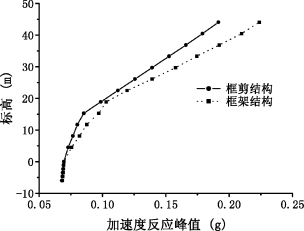
图5-11 不同结构形式时结构加速度反应峰值
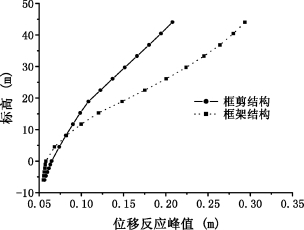
图5-12 不同结构形式时结构位移反应峰值
图5-13给出了不同上部结构形式时结构顶层加速度时程及其傅氏谱图,从加速度时程可进一步看出,框剪结构体系的加速度反应比框架结构体系的反应小。从傅氏谱图可看出,框剪结构相互作用体系的峰值频率要比框架结构相互作用体系的峰值频率大,这是由于框剪结构的刚度较大,从而导致相互作用体系自振频率较大。
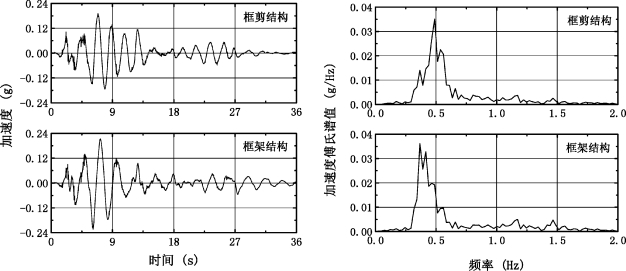
图5-13 不同上部结构形式时结构顶层加速度时程及其傅氏谱
3.不同上部结构形式时结构顶层位移组成分析
按第2.9节中图2-20和式(2-1)对本节相互作用体系的结构顶层位移反应组成进行分析,如表5-13所示。表中,u为结构顶层总位移,Hθ为基础转动引起的摆动位移,u g为基础平动引起的平动位移,ue为上部结构的弹性变形。
表5-13 不同上部结构形式时结构顶层位移组成分析(单位:m)
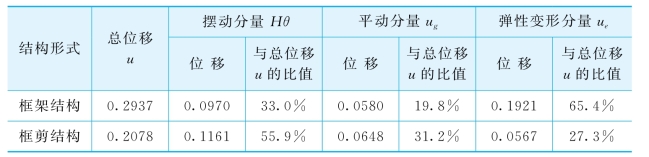
从表5-13可看出,当上部结构为框剪结构时,摆动分量Hθ占总位移u的比值和平动分量u g占总位移u的比值,比框架结构相应的比值要大,这主要是由于框剪结构的刚度比框架结构的刚度大,因而框剪结构时相互作用效果明显所致;而弹性变形分量ue与总位移u的比值,则比框架结构的相应比值小,这主要是由于框剪结构的刚度比框架结构的刚度大,因而弹性变形分量小而造成的。
4.不同上部结构形式时相互作用效果
(1)位移反应对比
表5-14给出了不同结构形式时结构沿振动方向的位移峰值比较,图5-14进一步给出了图形,从表5-14和图5-14中可看出,考虑相互作用后,上部结构的位移反应较不考虑相互作用时有所增加;且框剪结构增加的幅度要比框架结构大。这主要是由于框剪结构的刚度大,因而相互作用效果更加明显。这与文献[143]得出的结论是一致的。
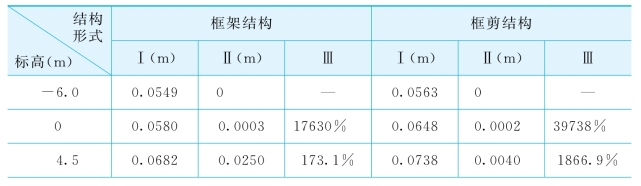
表5-14 不同上部结构形式时结构沿振动方向的位移峰值比较
续 表
 (https://www.xing528.com)
(https://www.xing528.com)
注:表中Ⅰ为考虑结构-地基动力相互作用时结构的位移峰值;Ⅱ为不考虑结构-地基动力相互作用时结构的位移峰值;Ⅲ为考虑与不考虑相互作用时结构位移峰值的相对误差,即为(Ⅰ-Ⅱ)/Ⅱ×100%。
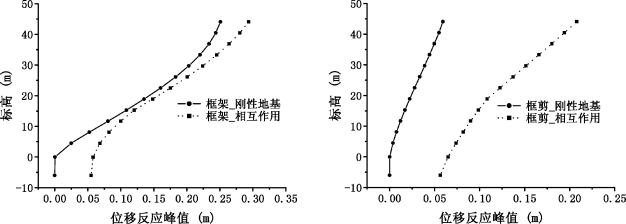
图5-14 不同上部结构形式时刚性地基与相互作用体系位移峰值反应比较
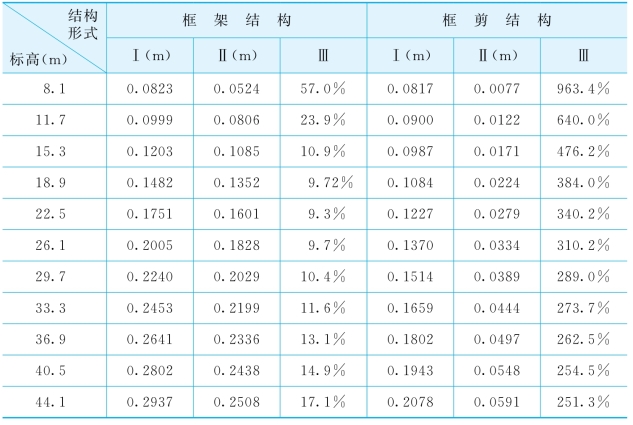
表5-15给出了不同上部结构形式时结构沿振动方向的层间位移峰值比较,图5-15进一步给出了图形,从表5-15和图5-15中可看出,考虑相互作用后,上部结构的层间位移较不考虑相互作用时有所增加;且框剪结构增加的幅度要比框架结构大。这主要是由于框剪结构的刚度大,因而相互作用效果更加明显所致。
表5-15 不同结构形式时结构沿振动方向的层间位移峰值比较
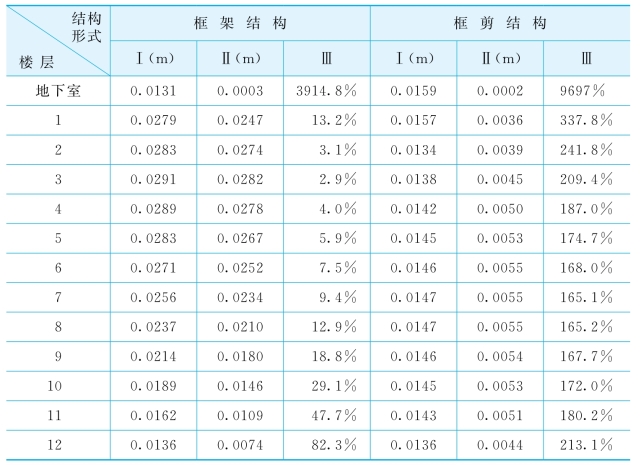
注:表中Ⅰ为考虑结构-地基动力相互作用时结构的层间位移峰值;Ⅱ为不考虑结构-地基动力相互作用时结构的层间位移峰值;Ⅲ为考虑与不考虑相互作用时层间位移峰值的相对误差,即为(Ⅰ-Ⅱ)/Ⅱ×100%。
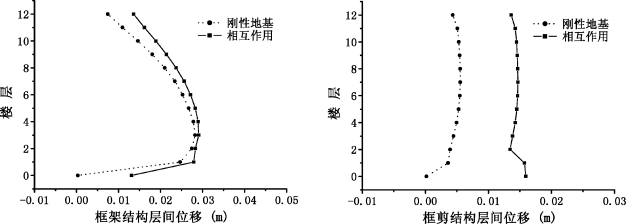
图5-15 不同上部结构形式时刚性地基与相互作用体系层间位移反应比较
(2)加速度反应对比
表5-16给出了不同上部结构形式时结构沿振动方向的加速度峰值比较,图5-16进一步给出了图形,从表5-16和图5-16中可看出,考虑相互作用后,上部结构的加速度反应较不考虑相互作用时有所减小,且框架结构的加速度反应及其变化幅度要比框剪结构的要大。这是因为地震波往上传播的过程中,高频分量被过滤,传到上部结构时低频分量已经占主导地位,而框架结构的频率比框剪结构的低,所以框架结构的加速度反应及其变化大。
表5-16 不同上部结构形式时结构沿振动方向的加速度峰值比较

注:表中Ⅰ为考虑结构-地基动力相互作用时结构的加速度峰值;Ⅱ为不考虑结构-地基动力相互作用时结构的加速度峰值;Ⅲ为考虑与不考虑相互作用时加速度峰值的相对误差,即为(Ⅰ-Ⅱ)/Ⅱ×100%。
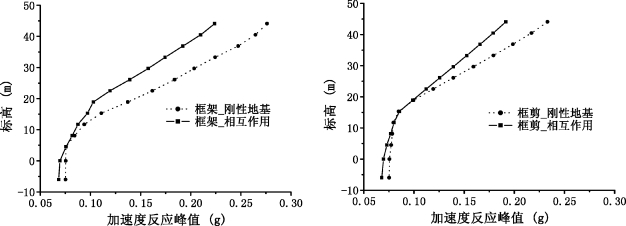
图5-16 不同上部结构形式时刚性地基与相互作用体系加速度反应比较
(3)层间剪力对比
表5-17给出了不同上部结构形式时结构沿振动方向的层间剪力比较,图5-17进一步给出了图形,从表5-17和图5-17中可看出,考虑相互作用后,上部结构的层间剪力较不考虑相互作用时有所减小,且框架结构的层间剪力及其变化幅度比框剪结构的要大。原因同“加速度反应对比”。
表5-17 不同上部结构形式时结构沿振动方向的层间剪力比较
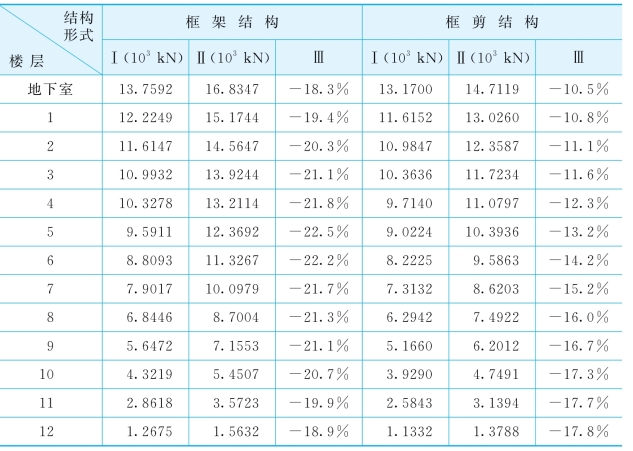
注:表中Ⅰ为考虑结构-地基动力相互作用时结构的层间剪力;Ⅱ为不考虑结构-地基动力相互作用时结构的层间剪力;Ⅲ为考虑与不考虑相互作用时层间剪力的相对误差,即为(Ⅰ-Ⅱ)/Ⅱ×100%。
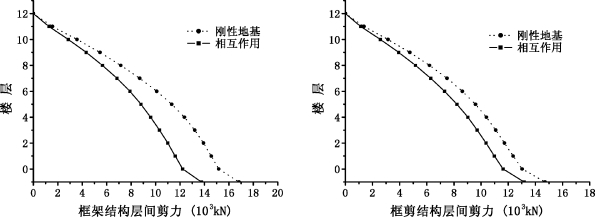
图5-17 不同上部结构形式时刚性地基与相互作用体系的层间剪力比较
(4)倾覆力矩对比
表5-18给出了不同上部结构形式时结构沿振动方向的倾覆力矩比较,图5-18进一步给出了图形,从表5-18和图5-18中可看出,考虑相互作用后,上部结构的倾覆力矩较不考虑相互作用时有所减小,且框架结构的倾覆力矩及其变化幅度大于框剪结构的倾覆力矩。原因同“加速度反应对比”。
表5-18 不同上部结构形式时结构沿振动方向的倾覆力矩比较
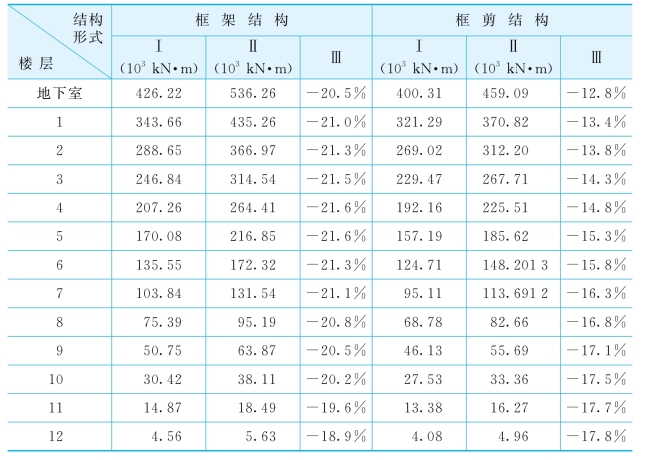
注:表中Ⅰ为考虑结构-地基动力相互作用时结构的倾覆力矩;Ⅱ为不考虑结构-地基动力相互作用时结构的倾覆力矩;Ⅲ为考虑与不考虑相互作用时倾覆力矩的相对误差,即为(Ⅰ-Ⅱ)/Ⅱ×100%。
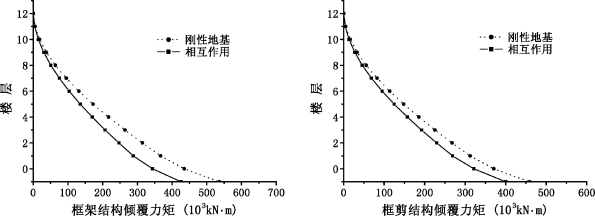
图5-18 不同上部结构形式时刚性地基与相互作用体系的倾覆力矩比较
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




