上部结构刚度对振动台试验的影响

本节通过改变上部结构的混凝土强度等级以及框架柱的尺寸来改变上部结构刚度，以研究上部结构刚度变化对SSI体系动力特性及相互作用效果的影响。

本书第5.2节“工程概况”中，上部框架结构采用C30混凝土，框架柱截面尺寸为600 mm×600 mm，为了研究上部结构刚度变化对相互作用特性的影响，选取如下五种情况进行计算：①混凝土强度等级为C20，框架柱截面尺寸为350 mm×350 mm，此时f s＜f g，即上部结构频率小于地基频率；②混凝土强度等级为C20，框架柱截面尺寸为450 mm×450 mm，此时f s＜f g；③混凝土强度等级为C20，框架柱截面尺寸为600 mm×600 mm，此时f s≈f g，即上部结构频率与地基频率基本一致；④混凝土强度等级为C30，框架柱截面尺寸为600 mm×600 mm，此时f s＞f g，即上部结构频率大于地基频率；⑤混凝土强度等级为C60，框架柱截面尺寸为700 mm×700 mm，此时，f s＞f g。

1.不同上部结构刚度时体系的自振频率

不同上部结构刚度时，相互作用体系的自振频率比较如表5-9所示。

表5-9　不同上部结构刚度时的自振频率比较

续 表

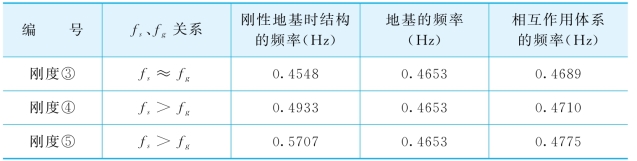
注：表中的频率均为X方向振型参与系数为最大时的频率。

从表5-9可看出，随着上部结构刚度的增加，相互作用体系的自振频率略有增加，且相互作用体系的自振频率与地基的自振频率较接近。可见，对本例而言，相互作用体系的自振频率更多的取决于地基土特性，受上部结构刚度变化的影响不大。

2.不同上部结构刚度时结构的加速度及位移反应

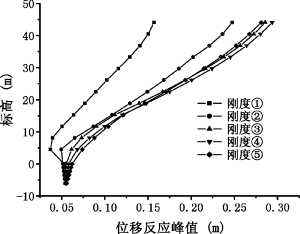
不同上部结构刚度时结构的加速度和位移反应峰值分别如图5-7和图5-8。从图5-7可看出，随着上部结构刚度的增加，上部结构的加速度反应也逐渐增加；从图5-8可看出，随着上部结构刚度的增加，上部结构的位移反应基本上也逐渐增加。文献[8]和文献[95]中指出上部结构的刚度越大，考虑相互作用后的位移就越大，本例计算结果基本符合这一观点。但是，当增大到一定程度以后，有可能随刚度增加，局部楼层位移反而减小。如图5-8，刚度⑤时顶部几层的位移略小于刚度③、④的相应位移，原因可能在于，楼层的位移是相互作用效果和刚度变化共同影响的，刚度增加导致的相互作用效果增加会使位移有增大趋势，而刚度增加本身又会使位移有减小的趋势，关键要看谁的作用更加明显。所以，对于具体问题应具体分析，并非如何情况下都是结构的刚度越大，考虑相互作用后的位移就越大。

图5-9给出了不同上部结构刚度时结构顶层加速度时程及其傅氏谱图。从加速度时程可进一步看出随着上部结构刚度的增加，结构的加速度反应增加。从傅氏谱图可看出，随着上部结构刚度的增加，傅氏谱图从多峰值变化为单峰值，再变化为多峰值，其中以刚度③时单峰值现象最明显，因为此时上部结构的自振频率与地基土的自振频率较接近，产生了共振现象。从傅氏谱图还可看出，随着上部结构的刚度增加，傅氏谱图中的峰值逐渐向右略有平移，体现了上部结构刚度的变化对相互作用体系基频的影响。

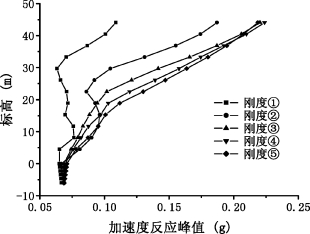
图5-7　不同结构刚度时结构加速度反应峰值

(www.xing528.com)

图5-8　不同结构刚度时结构位移反应峰值

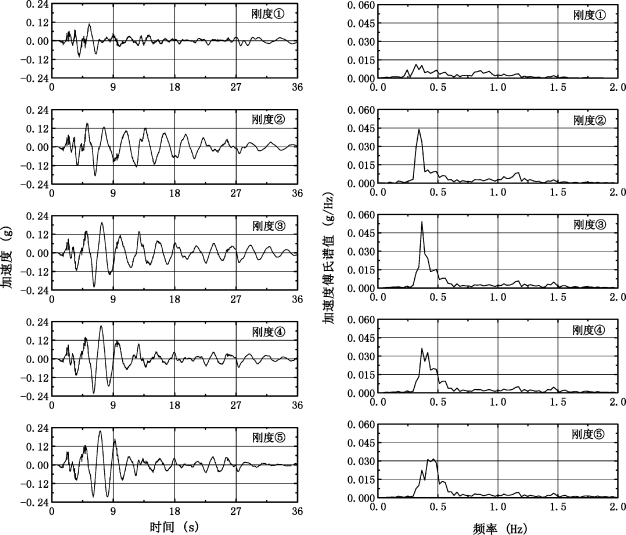
图5-9　不同上部结构刚度时结构顶层加速度时程和傅氏谱

3.不同上部结构刚度时结构顶层位移组成分析

按第2.9节中图2-20和式(2-1)对本节相互作用体系的结构顶层位移反应组成进行分析，如表5-10所示。表中，u为结构顶层总位移，Hθ为基础转动引起的摆动位移，u g为基础平动引起的平动位移，ue为上部框架结构的弹性变形。

表5-10　不同上部结构刚度时结构顶层位移组成分析(单位：m)

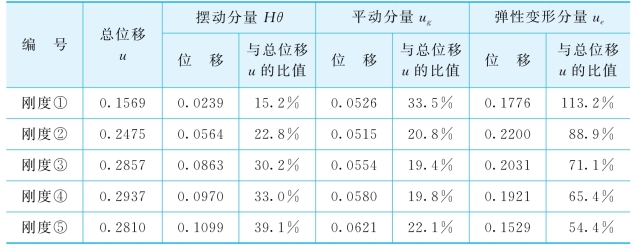
从表5-10可得出如下结论：

(1)摆动分量Hθ与总位移u的比值，随上部结构刚度的增加而增加。这说明随上部结构刚度的增加，相互作用效果更加明显，导致上部结构的转动分量增加。

(2)上部结构弹性变形分量ue与总位移u的比值，随上部结构刚度的增加而减小。从这里可看出，随上部结构刚度的增加，上部结构的转动分量增加，平动变形分量也略有增加，而弹性变形分量减小，总位移是这三部分共同作用的结果，并非单纯地随上部结构刚度的增加而增加。

4.不同上部结构刚度时的相互作用效果

对上部结构刚度为刚度③、刚度④和刚度⑤情况下考虑结构-地基动力相互作用的结构位移反应计算结果与刚性地基情况下的结果进行比较，如表5-11所示，表中刚性地基情况计算时结构底部输入的地震动是不同上部结构刚度时、考虑相互作用情况下得到的土表距离结构足够远处的加速度时程。

从表5-11可看出，上部结构刚度越大，相互作用对结构位移峰值的影响越显著，即上部结构刚度越大，相互作用效果越明显，这与文献[8]给出的结论是一致的。

表5-11　不同上部结构刚度时结构沿振动方向的位移峰值比较

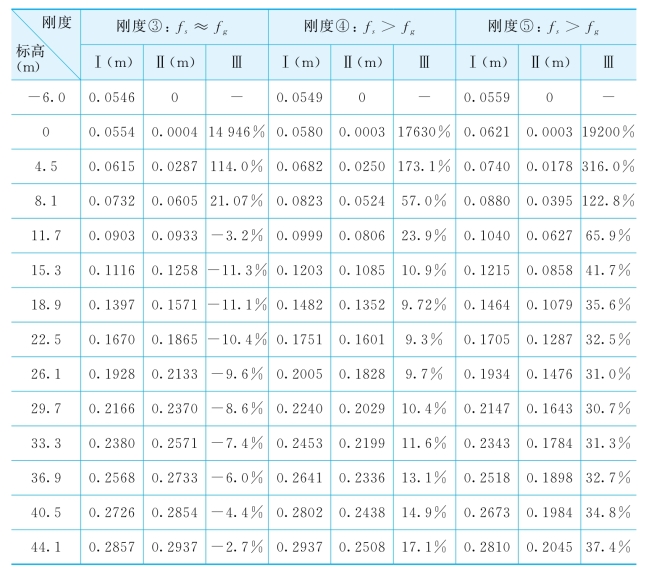
注：表中Ⅰ为考虑结构-地基动力相互作用时结构的位移峰值；Ⅱ为不考虑结构-地基动力相互作用时结构的位移峰值；Ⅲ为考虑与不考虑相互作用时结构位移峰值的相对误差，即为(Ⅰ-Ⅱ)/Ⅱ×100%。