对实际工程进行动力相互作用计算时,合理确定土体计算区域并正确施加人工边界,是计算模型能否正确、合理、有效地模拟实际工程的关键问题之一。本节以前面的建模方法为基础,分别建立了土体沿纵向和横向取不同边界长度的计算模型,探讨了纵向和横向边界取值对计算精度的影响,并讨论了在横向边界处施加粘-弹性人工边界的精度。其中,水平地震的输入方向定义为横向,水平面内垂直于地震输入方向定义为纵向。
1.纵向计算区域
本节在土体横向边界保持一定的前提下,进行了三种情况的计算:①土体取3倍结构纵向尺寸并采用自由边界;②土体取5倍结构纵向尺寸并采用自由边界;③土体取10倍结构纵向尺寸并采用自由边界。三种情况下,体系的动力特性比较如表5-5。
表5-5 不同纵向边界时相互作用体系的自振频率比较

三种情况下,从土体底部输入加速度峰值为0.1 g的El Centro波进行计算,所得位移峰值的比较见表5-6。表中A13是框架结构顶层中点,A1是结构底层中点,S19是结构正下方距土表41.3 m土中点,S25是沿地震输入方向距结构20 m处的土表点。
表5-6 不同纵向边界时的位移峰值比较
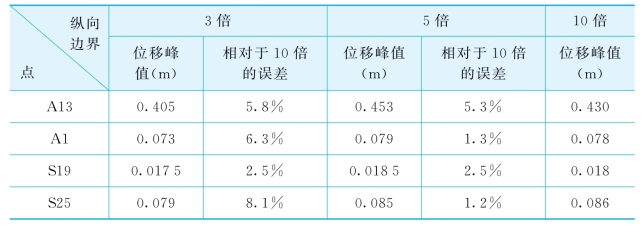
从表5-5和表5-6可以看出,纵向计算区域取值对相互作用体系的动力特性和位移反应的影响不大。当纵向边界取5倍的结构纵向尺寸时,纵向边界对相互作用体系的影响基本可以忽略。因而本书进行计算时,纵向边界选取了5倍的结构纵向尺寸。图5-4进一步比较了5倍和10倍纵向边界时,A13、A1、S19和S25点的位移时程,从图中可进一步看出纵向边界取5倍纵向尺寸,基本上可以消除纵向边界对相互作用体系影响。
2.横向计算区域
本节在土体纵向边界保持5倍结构纵向尺寸的前提下,进行了四种情况下的计算:①土体取10倍结构横向尺寸并采用自由边界;②土体取10倍结构横向尺寸并施加黏性边界;③土体取10倍结构横向尺寸并施加粘-弹性边界;④土体取30倍结构横向尺寸并取自由边界,利用此情况近似模拟半空间无限域。
 (https://www.xing528.com)
(https://www.xing528.com)
图5-4 不同纵向边界时位移时程比较
四种情况下,体系的动力特性比较如表5-7。从表中可以看出,四种情况下的相互作用体系的1阶、2阶频率接近。
表5-7 不同横向边界时相互作用体系的自振频率比较
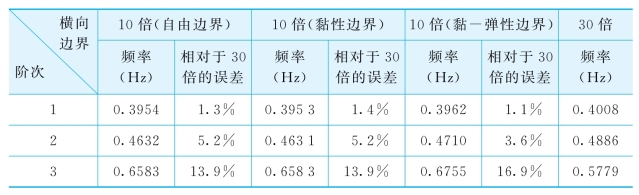
四种情况下,从土体底部输入加速度峰值为0.1 g的El Centro波进行计算,位移峰值的比较如表5-8。从表5-7和表5-8中可看出,10倍横向边界加黏性边界和黏-弹性边界都能较好的模拟无限域情况,且黏-弹性边界模拟的效果要比黏性边界稍好,这与第5.3.2节理论推导结果一致。因而在本书以后的计算中,横向边界选取10倍的结构横向尺寸,并在横向边界处施加黏-弹性人工边界。图5-5进一步比较了10倍横向边界加黏-弹性人工边界和30倍横向边界时,A13、A1、S19和S25点的位移时程,从图中可看出取10倍横向边界加黏-弹性人工边界和30倍横向边界的位移时程基本一致,从而进一步说明取10倍横向边界加黏-弹性人工边界进行计算基本上可以消除横向边界对相互作用体系的影响,可较好模拟无限域情况。
表5-8 不同横向边界时的位移峰值比较
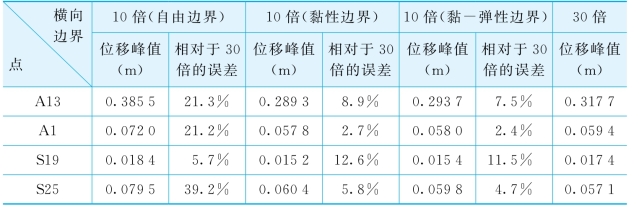
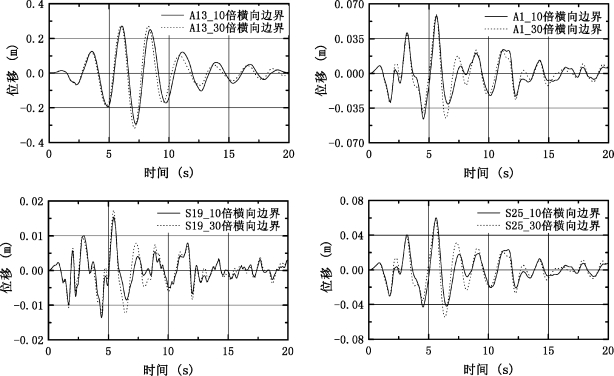
图5-5 不同横向边界时位移时程比较
综上所述,进行本例实际工程的计算时,土体纵向边界取5倍结构纵向尺寸,并在纵向边界处采用自由边界,土体横向边界取10倍结构横向尺寸,并在横向边界处施加粘-弹性人工边界,可较好地模拟无限域土体。图5-6给出了采用上述边界值的模型网格划分图,由于对称,图中沿地震波输入方向选取一半结构进行计算。图中,上部结构柱、梁采用梁单元模拟,箱基、楼板采用壳单元模拟,土体采用三维实体单元模拟。
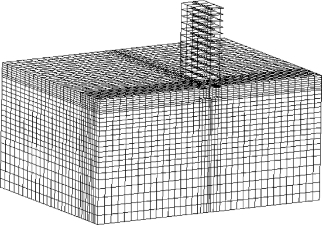
图5-6 网格划分图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




