常用的人工边界中,黏性边界、旁轴边界、透射边界属时域局部人工边界。其中,旁轴边界和透射边界精度较高,但旁轴边界最适合于有限差分析,透射边界由于直接模拟波动的传播,需要离散时间点和空间点上运动,易于与有限元和有限差分方法结合,但在实际工程中,由于高阶公式很复杂,并存在着稳定性问题,因此这两种边界常常也仅用到一阶精度。黏性边界虽然只有一阶精度,但概念清楚,易于程序实现,所以应用最为广泛。Deeks[141]采用与黏性边界推导过程相类似的方法,在假定二维散射波为柱面波的形式上推导出了黏-弹性人工边界条件。本章在计算分析中采用了这种黏-弹性人工边界,并在ANSYS程序中予以实现。
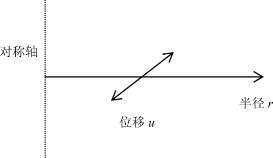
图5-2 推导过程所采用的坐标系
假定二维散射波为柱面波,坐标系如图5-2所示,出平面柱面波的运动方程为:
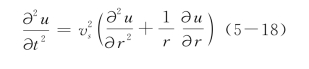
其中,u为介质的切向位移,vs为剪切波在连续介质中的传播波速:

其中,G为连续介质的剪切模量,ρ为介质的质量密度。
对于柱面波,精确的表达式不存在,可以近似地表达为下式[142]:

把f对它括号内变量的导数记为f′,则任一半径r上的剪应变和剪应力为:
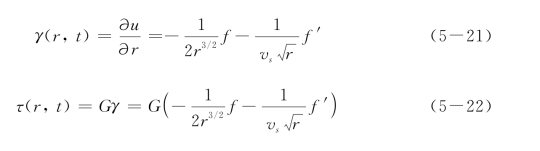
在任一半径rb处,导数f′和函数f对时间t的导数大小相等,符号也相同,因此该点的速度可表示为:
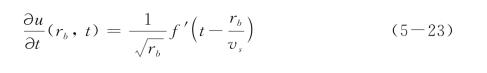
比较式(5-20)、式(5-22)和式(5-23)可知,任一半径rb处的应力同该处的速度和位移的关系可表示如下:
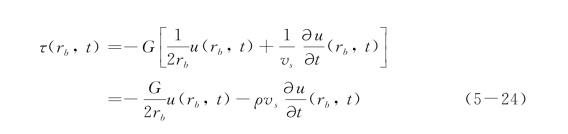
可以看出,方程(5-24)等价于一阻尼系数为ρv s的阻尼器(类似于黏性边界的黏性阻尼)并联上一个刚度系数为G/2rb的线性弹簧,这说明如果在半径rb处截断介质,同时施加相应的边界元件后,在边界上可以得到与方程(5-24)相同的形式,即可以完全消除满足方程(5-20)的剪切波在边界rb处产生的反射波,即可以精确地模拟满足方程(5-20)的剪切波由有限域向无限域的传播。但是,由于波动方程本身是近似满足运动方程(5-18)的,因此该边界方程也是近似成立的,它的精确程度依赖于波动方程(5-20)的近似程度。
人工边界的误差通常可以用反射系数R=B/A来表示,其中A和B分别表示入射波和由人工边界引起的反射波在人工边界处的幅值,如果|R|≤1,即所有边界节点上反射波的幅值均不超过入射波的幅值,那么,有限计算区中包含的全部能量不随反射次数增加,这样就可以保证数值计算不会发生失稳,并且R越小,人工边界的精度越高。
在边界上,实际波u(r)可以分为入射波u I(r)和反射波u R(r′)两部分,即u(r)=u I(r)+u R(r′)。其中:
入射波u I(r)的形式为:(https://www.xing528.com)
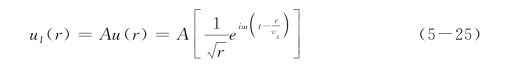
而反射波u R(r′)的形式为:
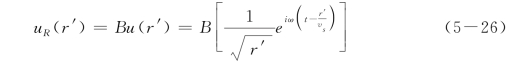
其中,ω为振动的角频率,θ为入射波传播方向与边界法线方向的夹角,即波入射角。在这里,为方便起见,入射波和反射波选用了不同的坐标系r和r′,两个坐标系的原点关于边界点是对称的,因此反射波的形式与入射波的形式是相同的。
在边界点处,r=rb,r′=rb,因而有边界条件:
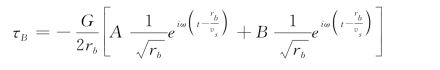

而入射波和反射波产生的应力分别为:
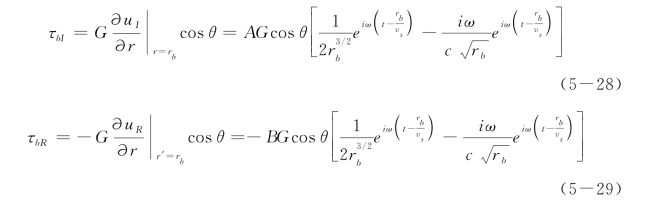
由τB=τb=τbI+τb R得:
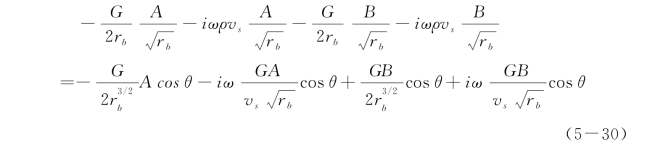
简化后,可得出黏-弹性边界的反射系数如下:
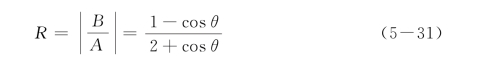
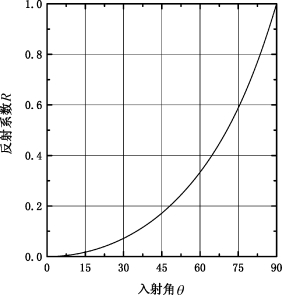
图5-3 反射系数与入射角的关系
式(5-31)的形式与Lysmer黏性边界的形式相同,即黏-弹性人工边界的反射系数R也随入射角θ的变化而变化,R与θ的关系如图5-3所示,当入射角θ为0°(即入射波垂直入射)时,反射系数R=0,这说明在边界上不存在反射波,即此时黏-弹性人工边界条件精确满足方程(5-20),这一点可由其推导过程显然得到。当入射角θ为90°时,即入射波平行边界入射时,R=1,此时黏-弹性人工边界的误差最大。
从上面的分析结果看,黏-弹性人工边界与黏性边界的精度相同,但是,由于推导粘-弹性人工边界时对散射波场的假设更符合实际情况,因此实际上黏-弹性人工边界的精度要高于黏性边界,这一点可从第5.4.1节的算例中清楚地看出。
在三维波的传播问题中,边界面上要施加三个方向的边界元件,边界的法线方向需施加阻尼器,阻尼系数为ρv p;在边界的切线方向,需同时施加并联的阻尼器和线性弹簧,阻尼器的阻尼系数为ρvs,线性弹簧的刚度系数为G/2rb。
在ANSYS程序中施加黏-弹性边界时,利用程序中的弹簧-阻尼单元,在每一节点处施加三个方向的边界元件。由于ANSYS程序中的弹簧-阻尼单元利用的是集中阻尼和集中弹簧的概念,因此每个元件的阻尼系数和刚度系数要乘以该元件所在节点的支配面积。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




