土体动力本构模型选取技巧

本章在进行土-箱基-结构动力相互作用体系的计算中，土体采用等效线性化模型。等效线性化方法和真线性方法是目前地基抗震中考虑土介质非线性动力性能的两种主要方法。等效线性化的基本思想是根据土的动剪切模量G与阻尼比D随剪应变幅值γ之间的关系，通过叠代法得到使G、D与γ相协调的等效线性体系，以近似求解土的非线性动力反应。真非线性方法则按照土在任意往返荷载下的非线性应力应变关系，遵循实际应力路径进行增量分析求解。自1969年，Seed和Idriss首次用等效线性化方法计算了水平场地的地震反应以来，等效线性化方法在工程中得到广泛应用。Martin和Seed对六个一维场地，分别用等效线性化方法和两种非线性本构模型的真非线性方法进行对比分析，研究表明等效线性化方法和真非线性方法结果基本一致[135]。Hadjian用台湾Lotung核电站模型的地震观测记录对一些程序进行测试，表明等效线性化方法用于地基地震反应和土-结构动力相互作用是可行的[82-83]。

试验研究表明，土的动剪切模量G与动剪应变幅值γ之间的关系基本符合双曲线关系，土的阻尼比D也随剪应变幅值γ变化。1972年，Hardin和Drnevich提出了预测G/G max～γ和D/D max～γ之间关系的经验关系，即著名的Hardin-Drnevich模型，如式(5-1)所示：

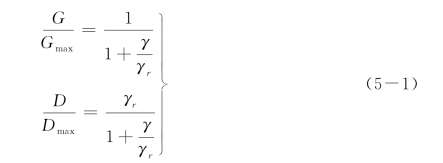
式中，G max、D max分别是最大动剪切模量和最大阻尼比，可以通过试验或经验公式确定，为参考剪应变，τmax为γ足够大时以土的抗剪强度为渐近线的极限值，一般可以取γ=0.01时的τ值。对于剪应力τ作用于水平面上的情况，可以近似地根据莫尔-库仑破坏理论按式(5-2)计算：

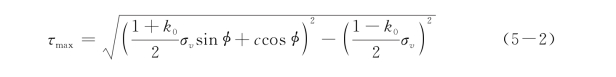
式中，k 0为静止土压力系数，σv为土承受的静止竖向正应力，c和φ分别为土的内聚力和内摩擦角。

为了更好地符合试验结果，可以引入两个经验参数a和b，并把模型中的γr换为γh，γh由下式计算：

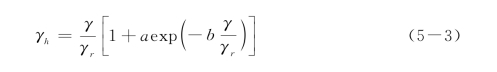
后来，Seed和Martin改进了Hardin-Drnevich模型，认为Davidenkov模型可以更好地描述各类土剪应力与剪应变之间的关系。

在此基础上，本章采用Davidenkov模型的土骨架曲线，G/G max～γ关系如式(5-4)所示：

其中，

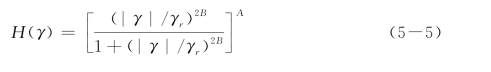
式中各参数的意义与前面相同，当参数A=1.0、B=0.5时与Hardin-Drnevich模型相同。

对于土的滞回曲线D/D max～γ，根据有关试验结果可以用如下经验公式表示：

其中，D max为最大阻尼比，β为D～γ曲线的形状系数，对于大多数土，β的取值在0.2～1.2之间，对于上海软土可取1.0。

下面针对上海土的上述Davidenkov模型中的参数：最大动剪切模量G max、最大阻尼比D max以及A、B、γr的取法作一简单介绍。

1.最大动剪切模量G max

最大动剪切模量G max可用共振柱法测定，也可由经验公式求出。Hardin、Richart、Black等人提出了大多数黏土和砂的G max可以用下列经验公式计算。

对于圆粒干净砂(e＜0.8)

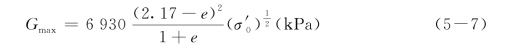
对于角粒干净砂

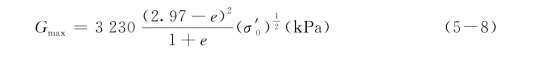
对于黏性土

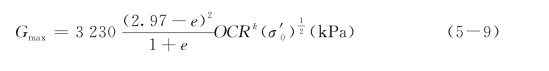
式中，e是孔隙比，σ′0是土的平均有效固结应力，OCR是土的超固结比，k是塑性指数I p有关的参数，当I p=0，20，40，60，80和I p≥100时，k分别取0，0.18，0.30，0.41，0.48，0.50。

王天龙[136]通过室内共振柱试验证明，上述公式对于上海土层，包括深层土仍然有效。费涵昌根据上海某大桥桥址土层的共振柱试验，对以上公式的系数进行了部分修正：

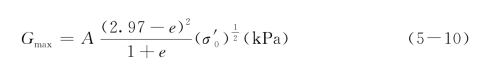(www.xing528.com)

其中，A为试验参数，对于黏土、亚黏土，A=3000；对于轻亚黏土，A=4000；对于粉细砂，A=7000。

后来，Hardin等又修正了以上公式，提出了适用于各类土的经验关系

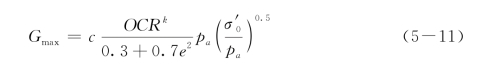
式中，c是与土类有关的试验常数，p a为标准大气压，其他参数意义同上。

黄雨[137]等以式(5-11)为基础，通过对上海土层共振柱试验资料的分析，提出了以下G max经验关系式

其中，对于黏性土c=353.2，粉性土c=450.7，砂性土c=485.4。应该指出：由于上海土除了表层硬壳层、暗绿色硬土层等是超固结土外，以黏土、淤泥质黏土为主的上海土层是微超固结土层，平均的OCR≈1.10，因此可近似看作正常固结土。

G max也可根据现场地球物理试验，用波速法确定，如式(5-13)所示。

式中，ρ为土的质量密度，V s为土的剪切波速。

上海市地基基础设计规范[133]提供了上海部分土层的剪切波速参考值及由标准贯入试验击数N和土层深度z计算V s的经验公式，如表5-2和式(5-14)：

表5-2　上海部分土层的剪切波速Vs值

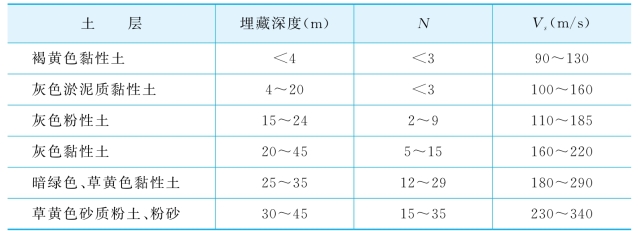
注：(1)浅层土N较低时，剪切波速V s取低值；(2)表中N系现场实测值，未经深度修正。

式中，α为系数，褐黄色黏性土α=0.75；暗绿色、草黄色黏性土α=1.20；草黄色砂质粉土，粉砂α=1.35；其他类土α=1.00；z的单位为m。

周锡元[138]提出上海地区土层深度z与剪切波速V s的统计关系为：

金华[139]提出上海地区土层的V s～z的统计关系为：

郑金安[140]对上海第四系土的剪切波速、动剪切模量与深度的关系进行了比较详细的研究，提出了统计关系式，见表5-3。

2.最大阻尼比D max以及参数A、B、γr

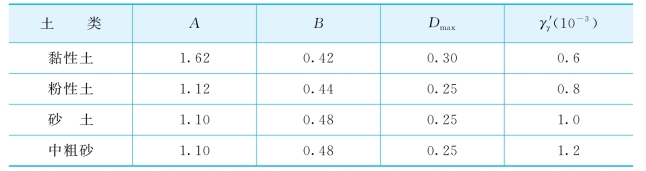
上海土层Davidenkov模型的土骨架曲线G/G max～γ关系式的参数A，B及最大阻尼比D max可参考表5-4选用。另外一个参数γγ则可按照式(5-17)确定。

表5-3　上海第四系土的剪切波速、动剪切模量与深度统计关系

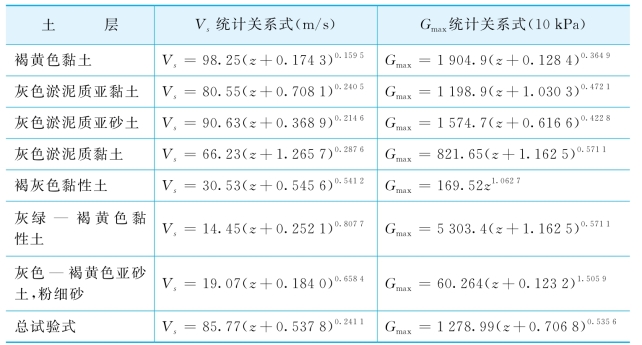
表5-4　上海土层Davidenkov模型的参数