1.求最大弯矩
如图3-2-30的单梁桥式吊车可以简化为受集中力(Q+G)的简支梁，由上述内容可知，其最大弯矩在梁的中点，且
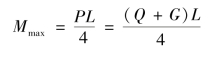
2.进行强度校核
由强度条件
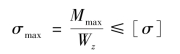
由已知条件可知梁的抗弯截面模量Wz=1 430 cm3
所以
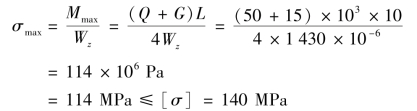
所以该梁强度符合要求。
(1)杆轴线由直线变成曲线，这种变形称为弯曲变形。
(2)梁的类型:简支梁、外伸梁、悬臂梁。
(3)弯矩:力偶矩M称为弯矩，M(x)=-Fl。
(4)弯曲强度校核: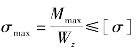
。
一、填空题
(1)构件的承载能力主要由________、________、和________3个因素来衡量。
(2)轴向拉伸或者压缩杆件，其受力特点是:________________________；其变形特点是____________________。
(3)构件在外力作用下，________称为应力；如果拉(压)杆的应力垂直横截面，则该应力称为________；应力的国际单位为________。
(4)构件受剪切作用是的受力特点是:____________________。
(5)挤压作用是指______________的现象，而______________面就叫作挤压面，用符号________表示。
(6)长度和截面面积相同的两杆，一是钢杆，一是铜杆，若受同样大小的拉力的作用，则两杆的内力________，应力________，变形________，许用应力________。
二、选择题
(1)在校核材料的剪切和挤压强度时，当其中有一个超过许用值时，强度________。
A.不够 B.足够 C.无法判断
(2)圆轴扭转时，横截面上________。
A.有正应力，其大小与截面直径无关
B.有正应力也有剪应力，它们的大小均与截面直径无关
C.只有剪应力，其大小与到圆心的距离成正比
三、计算题
(1)试用截面法求3-2-35中各杆指定截面的轴力，并作出轴力图。
图3-2-35 画杆的轴力图
(2)试求图3-2-36中各轴在指定横截面1-1、2-2和3-3上扭矩。
图3-2-36 圆轴的扭矩
(3)试绘出图3-2-37中各轴的扭矩图。
(www.xing528.com)
图3-2-37 作轴的扭矩图
(4)如图3-2-38所示，传动轴转速n=250 r/min，轮B输入功率PB=7 kW，轮A、C、D输出功率为PA=3 kW，PC=2.5 kW，PD=1.5 kW，PB=7 kW，试绘该轴的转矩图。
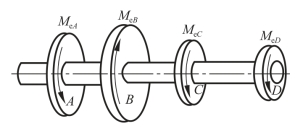
图3-2-38 传动轴
(5)如图3-2-39所示，试计算下列各梁指定横截面的剪力和弯矩。
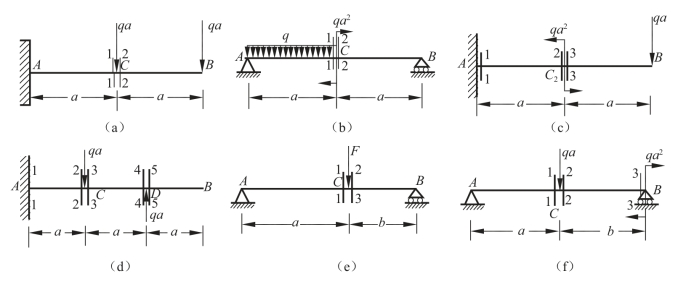
图3-2-39 求梁的剪力和弯矩
(6)如图3-2-40所示，试作出下列各梁的弯矩图，并求出|M|max。
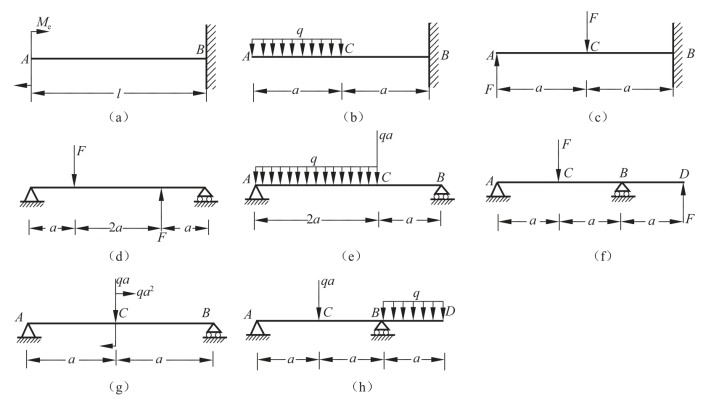
图3-2-40 画梁的弯矩图
(7)如图3-2-41所示，试作出下列各梁的弯矩图，求出其|M|max，并加以比较说明。
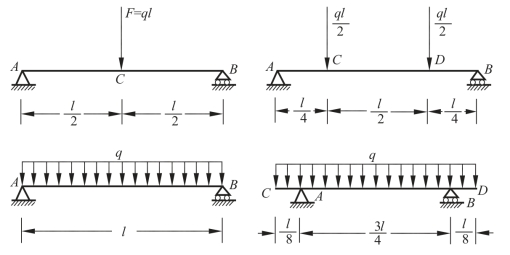
图3-2-41 画梁的弯矩图
(8)三种材料的σ-ε曲线如图3-2-42所示，试指出这三种材料的机械性能特点。
(9)判断图3-2-43所示的横截面上的切应力分布图是否正确。
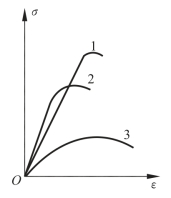
图3-2-42 σ-ε曲线
图3-2-43 切应力分布图
(10)简述弯曲正应力公式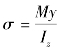
中各符号的含义，σ的正负号的确定及公式应用的范围。
(11)试比较圆形、矩形和工字形截面梁的合理性。
(12)求图示3-2-44阶梯杆横截面1-1，2-2，3-3上的轴力，并作轴力图。若横截面面积A1=200 mm2，A2=300 mm2，A3=400 mm2，求各横截面上的应力。
(13)图示3-2-45为由两种材料组成的圆杆，直径d=40 mm，杆的总伸长Δl=0.126 mm。试求载荷F及杆内的最大正应力。
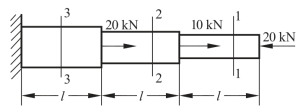
图3-2-44 阶梯轴横截面
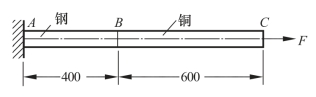
图3-2-45 两种材料组成的圆杆
(14)一传动轴如图3-2-46所示，已知MeA=1.3 N·m、MeB=3 N·m、MeC=1 N·m、MeD=0.7 N·m；各段轴的直径分别为:DAB=50 mm、DBC=75 mm、DCD=50 mm。试绘转矩图并求1-1、2-2、3-3截面上的最大切应力。
(15)如图3-2-47所示，铆接钢板厚t=10 mm，铆钉直径d=17 mm，铆钉的许用切应力[τ]=140 MPa，许用挤压应力[σbs]=320 MPa，载荷F=24 kN，试对铆钉强度进行校核。
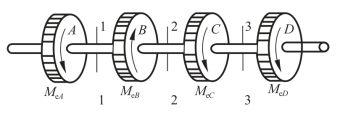
图3-2-46 传动轴
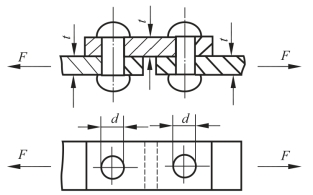
图3-2-47 铆钉连接
16.悬臂梁受力及截面尺寸如图3-2-48所示。设q=60 kN/m，F=100 kN。试求
(1)梁1-1截面上A、B两点的正应力；
(2)整个梁横截面上的最大正应力。
17.简支梁受力如图3-2-48所示。梁为圆截面，其直径d=40 mm，求梁横截面上的最大正应力。
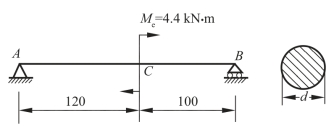
图3-2-48 简支梁的受力
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
