汽车机械基础第2版：直梁弯曲的应力和变形

1.纯弯曲时梁横截面上的正应力

图3-2-32所示的梁CD段为纯弯曲变形，该段横截面上的正应力的分布规律也需从几何、物理和静力学三方面考虑，详细分析请参考有关教材。

对弯曲变形的变形特点做出的平面假设认为:原为平面的横截面变形后仍保持为平面，且仍垂直于变形后梁的轴线，只是绕横截面内某一轴旋转了一角度(图3-2-33(b)、(c))。若设想梁由无数纵向纤维组成，所有纵向纤维只受到轴向拉伸与压缩，由变形的连续性可知，从梁上半部的压缩到下半部的伸长，其间必有一层长度不变，该层称为中性层，中性层与横截面的交线，称为中性轴(图3-2-33(c))。

图3-2-32　梁的纯弯曲变形

2.正应力的分布规律

经理论分析，知中性轴通过横截面的形心。变形时横截面绕其中性轴转动。由上述三方面的分析可得1/ρ=M/EIz，以及纯弯曲时梁横截面上的正应力计算公式

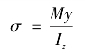
式中　M——横截面上的弯矩，N·m；

y——横截面上任一点到中性轴的距离；

Iz=∫A y2dA——截面对中性轴z的惯性矩，只与截面的形状和尺寸有关的几何量。(www.xing528.com)

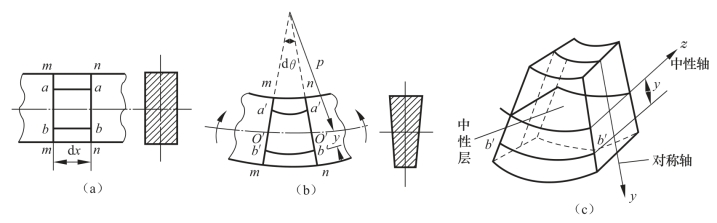
图3-2-33　中性层和中性轴

(a)未受力；(b)受力变形后；(c)中性层和中性轴

由上式可知，梁弯曲时，横截面上任一点处的正应力与该截面上的弯矩成正比，与惯性矩成反比，并沿截面高度呈线性分布。

y值相同的点，正应力相等；中性轴上各点的正应力为零。在中性轴的上、下两侧，一侧受拉，一侧受压。距中性轴越远，正应力越大(图3-2-34)。

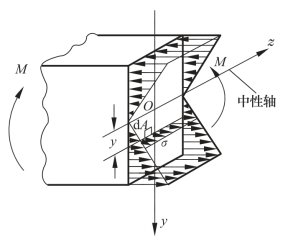
图3-2-34　梁截面正应力分布规律

当y=ymax时，弯曲正应力最大，其值为

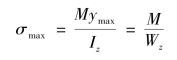
式中，Wz=Iz/ymax称为截面对于中性轴的抗弯截面模量，单位mm3，Wz是一个与截面形状和尺寸有关的几何量，反映梁横截面抵抗弯曲破坏能力。