1.扭矩
为了确定扭转时横截面上的内力,仍采用截面法。图3-2-23(a)为处于平衡状态下的两端垂直于轴线平面内受一对等值、反向的外力偶作用的圆轴。
若求任意横截面n-n上的内力,假想沿截面将轴切开,分为左右两段,任取左或右段为研究对象,现取左段为研究对象(图3-2-23(b)),由于左端有外力偶作用,在n-n截面上必有一个内力偶T与之相平衡。

图3-2-23 扭矩的计算
(a)轴的受力图;(b)轴的左段;(c)轴的右段
由平衡方程ΣMx=0,T-Me=0
有
T=Me
因此,圆轴扭转时,其任意横截面上的内力为一个作用在该截面上的力偶,称为扭矩。用T表示。
若取右段为研究对象,结果相同。
为了使截面两侧求出的转矩具有相同的正负号,采用右手螺旋法则:四指转向为圆轴转向,以右手拇指表示为转矩矢量,背离该截面时为正,指向该截面时为负。这样无论取左段或右段,其横截面上的转矩正负号均相同。
与求轴力的方法相类似,用截面法计算转矩时,可将转矩设为正值,计算结果为负说明该转矩转向与所设的转向相反。
2.扭矩图
为了清楚看出各截面扭矩的变化情况,以便确定危险截面,通常把扭矩随截面位置的变化绘成图形,称为扭矩图。扭矩图的绘制是以横坐标表示截面位置,以纵坐标表示相应截面的扭矩。把扭矩的计算结果按适当比例绘于图上,即得扭矩图。如图3-2-24(e)所示。
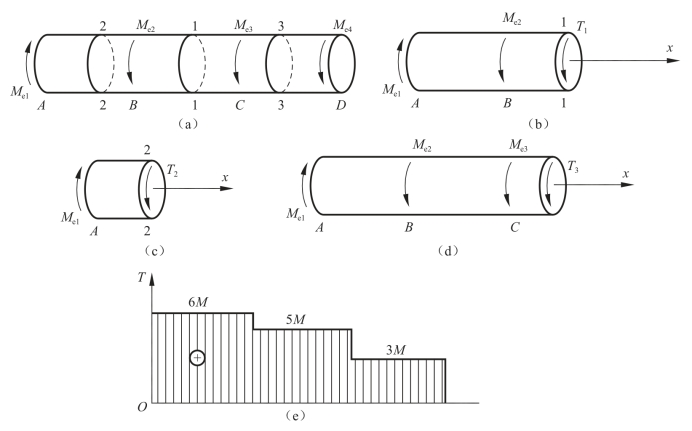
图3-2-24 圆轴
(a)圆轴受力图;(b)、(c)、(d)受力分析图;(e)扭矩图
例3-4 图3-2-25所示为一传动轴,主动轮B输入功率PB=60 kW,从动轮A、C、D输出功率分别为PA=28 kW,PC=20 kW,PD=12 kW。轴的转速n=500 r/min,试绘制轴的扭矩图。(https://www.xing528.com)
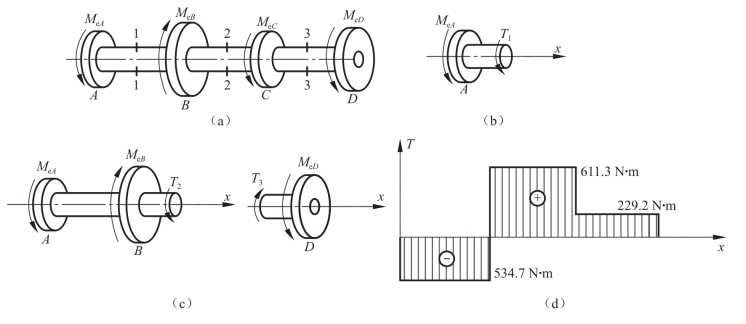
图3-2-25 传动轴
(a)传动轴受力图;(b)、(c)分析图;(d)扭矩图
解:1)计算外力偶矩
由式![]() 得
得
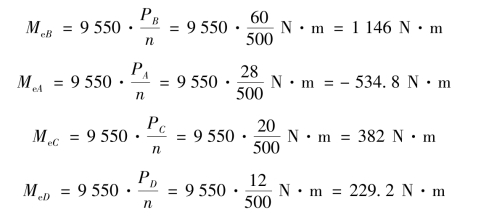
2)计算转矩
应用截面法求出各截面上的转矩,得
AB段
T1=∑Me=-MeA=-534.8 N·m
BC段
T2=∑Me=MeB-MeA=1 146-534.8=611.2 N·m
CD段
T3=∑Me=-MeD=229.2 N·m
3)画转矩图
根据以上计算结果,按比例画扭矩图,由图可知,最大转矩在BC段内的横截面上,其值为611.2 N·m。
4)讨论
若将AB两轮位置互换一下,再分析其内力转矩,与上述分析有何不同的结果?
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




