1.力系
物体处于平衡状态时，作用于该物体上的力系称为平衡力系。力系平衡所满足的条件称为平衡条件。如果两个力系对同一物体的作用效应完全相同，则称这两个力系互为等效力系。当一个力系与一个力的作用效应完全相同时，把这一个力称为该力系的合力，而该力系中的每一个力称为合力的分力。
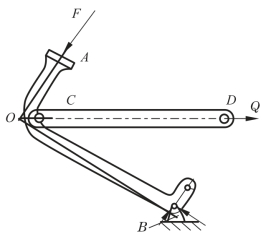
图3-1-15 汽车制动操纵装置
必须注意，等效力系只是不改变原力系对于物体作用的外效应，至于内效应显然将随力的作用位置的改变而有所不同。
2.刚体
所谓刚体是指在受力状态下保持其几何形状和尺寸不变的物体。显然，这是一个理想化的模型，实际上并不存在这样的物体。但是，工程实际中的机械零件和结构构件，在正常工作情况下所产生的变形，一般都是非常微小的。这样微小的变形对于研究物体的外效应的影响极小，是可以忽略不计的。当然，在研究物体的变形问题时，就不能把物体看作是刚体，否则会导致错误的结果，甚至无法进行研究。
3.力在坐标轴上的投影
过F两端向坐标轴引垂线(图3-1-16)得垂足a、b、a′、b′。线段ab和a′b′分别为F在x轴和y轴上投影的大小，投影的正负号规定为:从a到b(或从a′到b′)的指向与坐标轴正向相同为正，相反为负。F在x轴和y轴上的投影分别计作Fx、Fy。
4.三力平衡汇交定理应用
物体受三个力作用而平衡时，此三个力的作用线必汇交于一点，此推论称为三力平衡汇交定理。如图3-1-17所示的钢架受力分析，钢架受3个力P、RA、RC的作用处于平衡状态。其中，P为已知力，方向水平向右；RA，RC属于约束反力，其中RC垂直于支撑面，而RA的方向未定。由三力平衡汇交定理可推知，RA的作用线必通过P和RC作用线的交点E，如图3-1-17所示。
(www.xing528.com)
图3-1-16 力在坐标轴上的投影
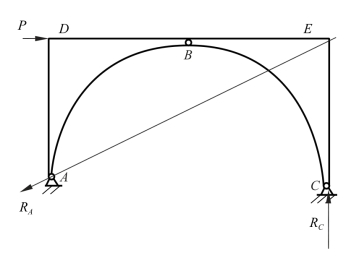
图3-1-17 钢架受力分析
5.平面交汇力系平衡的几何条件
力的多边形法则:利用几何法求解未知力时，只要将力系中各力依次首尾相接地连成折线，然后用一有向线段连接折线的首末两点，即可以获得一封闭图形，封闭边即为该力系的合力。如图3-1-18所示。
在图3-1-18中，平面汇交力系F1、F2、F3、F4已合成为一个合力FΣ。若在该力系中另加一个力F5，使其与力FΣ等值、反向、共线，则根据二力平衡公理可知，物体处于平衡状态，即F1、F2、F3、F4、F5成平衡力系。如做出该力系的力多边形，将成为一个封闭的力多边形，即最后一个力的终点与第一个力的起点相重合，亦即该力系的合力为零(图3-1-19)。因此，平面汇交力系平衡的必要与充分条件为力系的合力等于零；其几何条件为力系中各力所构成的力多边形自行封闭。用矢量表达式为
FΣ=0 或 ΣFi=0
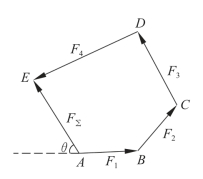
图3-1-18 力的多边形法则
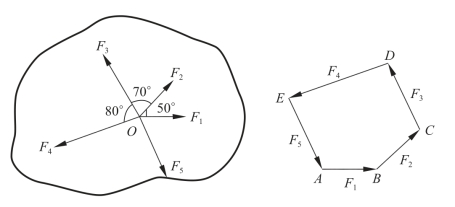
图3-1-19 平面汇交力系平衡的几何条件
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
