1.画推杆的受力图
(1)选取研究对象。选推杆BE为研究对象,画出它的简图。
(2)受力分析。推杆BE受油缸对它的推力和翻斗对它的作用力,是一个二力构件,并处于平衡状态。推杆受力情况要通过二力平衡公理确定。
二力平衡公理:刚体只受两个力作用而处于平衡状态时,这两个力的大小相等,方向相反,而且作用在同一条直线上。
因此推杆BE在油缸E处受到的力FE,方向由E指向B;在B处受到翻斗的约束反力FB,方向由B指向E。两个力的大小相等,都等于油缸对推杆的推力500 N,方向相反,作用在一条直线上。
(3)画受力图。画推杆BE的受力图,如图3-1-13所示。
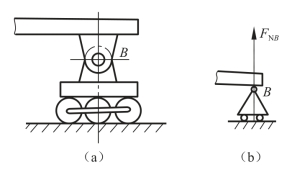
图3-1-12 活动铰链支座
(a)实物图;(b)受力图
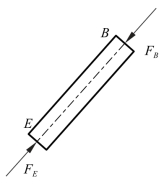
图3-1-13 推杆BE的受力图
2.画翻斗的受力图
(1)选取研究对象。选翻斗为研究对象,画出它的简图。
(2)受力分析。翻斗受到三个力的作用:翻斗自身重力G,作用于翻斗的重心,力的方向竖直向下,大小为1 200 N;铰链B为外约束,对翻斗的约束反力为RB;铰链A为外约束,对翻斗的约束反力为RA。
首先确定B处的约束反力RB。铰链B存在着推杆BE和翻斗之间的作用力与反作用力。铰链B对翻斗的作用力要通过作用与反作用公理来确定。
作用与反作用公理:两个物体间的作用力与反作用力总是成对出现,分别作用在两个物体上,且大小相等,方向相反,在同一条直线上。
根据作用力与反作用力公理和推杆BE受力情况,已知推杆BE受到翻斗的作用力FB,方向沿推杆方向,大小等于油缸对推杆的作用力即FE为500 N,所以推杆BE对翻斗的作用力RB方向与FB相反,大小与FB相等即为500 N,且与FB在同一条直线上,作用于翻斗上B点。
其次确定A处的约束反力RA。铰链A处对翻斗的约束反力RA通过铰链A的中心,翻斗受到的G、RB、RA三个力作用处于平衡状态。所以,铰链A对翻斗的作用力RA的方向可以通过三力平衡汇交定理来确定。
三力平衡汇交定理:若作用于物体同一平面上的三个不平行的力构成平衡力系,则它们的作用线必汇交于一点。
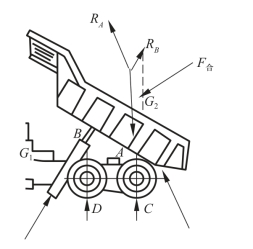
翻斗受到G、RB、RA三个力作用处于平衡状态,这3个力在同一平面内,所以RA的作用线必通过G、RB两作用力的交点O和A,如图3-1-14所示。
 (https://www.xing528.com)
(https://www.xing528.com)
图3-1-14 翻斗的受力图
翻斗受到G、RB、RA三个力作用交汇于一点,可以用力的平行四边形法则进行合成。
力的平行四边形法则:作用于物体上同一点的两个力,可以合成一个合力。合力也作用于该点,合力的大小和方向,用这两个力为邻边所构成的平行四边形的对角线确定。
翻斗受到G,RB,RA三个力作用处于平衡状态。所以这三个力的合力为零。RA必定与G和RB的合力成为一对平衡力。可以先对G=1 200 N与RB=500 N用平行四边形法则合成,RA必定与其合力的大小相等方向相反,且在同一条直线上。
(3)画受力图。画翻斗的受力图,如图3-1-14所示。
![]()
1.基本概念
(1)力是物体之间相互的机械作用:力的效应有外效应和内效应,静力学中研究力的外效应。力对物体的外效应,决定于三要素:大小、方向和作用点。
(2)力系是作用在同一物体上的若干个力的总称。
(3)刚体是静力学中将实际物体进行抽象化的理想模型。静力学的研究对象是刚体。
(4)平衡在工程上一般是指物体相对于地面保持静止或做匀速直线运动的状态。
2.静力学公理及其推论反映了力的基本性质
二力平衡公理:刚体只受两个力作用而处于平衡状态时,这两个力的大小相等,方向相反,而且作用在同一条直线上。
作用与反作用公理:两个物体间的作用力与反作用力总是成对出现,分别作用在两个物体上,且大小相等,方向相反,在同一条直线上。
三力平衡汇交定理:若作用于物体同一平面上的三个不平行的力构成平衡力系,则它们的作用线必汇交于一点。
力的平行四边形法则:作用于物体上同一点的两个力,可以合成一个合力。合力也作用于该点,合力的大小和方向,用这两个力为邻边所构成的平行四边形的对角线确定。
3.物体的约束及受力分析
(1)柔体约束:这种约束只能承受沿柔体方向的拉力。
(2)光滑面约束:这种约束只能承受位于接触点的法向压力。
(3)光滑铰链约束:可分为固定铰支座、中间铰链、活动铰链支座三种形式,前两种能限制物体两个方向的移动,故表示为正交约束反力;第三种的约束反力只能位于滚子接触面的法线方向。
(4)在解除约束的分离体上,画上它所受的全部主动力和约束反力,就称为该物体的受力图。画受力图时应注意:只画受力,不画施力;只画外力,不画内力;解除约束后,才能画上约束反力。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




