汽车机械基础：渐开线齿轮齿廓与传动比

1.渐开线的形成

当直线AB沿半径rb的圆作纯滚动时，直线上任一点K的轨迹DKE，称为该圆的渐开线。该圆被称为基圆，该直线被称为发生线，如图1-4-13所示。

以同一基圆上产生的两条相反的渐开线为齿轮的齿廓，即为渐开线齿轮。

图1-4-13　渐开线的形成

动画1-32　渐开线形成

动画1-33　渐开线的性质动画组

2.渐开线的性质

(1)发生线沿基圆滚过的线段长度等于基圆上被滚过的弧的长度。

(2)渐开线上任意点K的法线与基圆相切，同理渐开线上各点的法线都与基圆相切。

(3)渐开线的形状决定于基圆大小。同一基圆上的渐开线形状完全相同。基圆越大，渐开线越平直，当基圆半径为无穷大时，渐开线成为直线。

(4)基圆内部无渐开线。

3.渐开线方程

渐开线的形成，如图1-4-14所示。

压力角

αK=∠NOK

△ONK中:

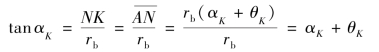
即

θK=tan αK-αK

θK称为角αK的渐开线函数，使用inv αK表示θK。

即θK=invαK=tan αK-αK

渐开线方程

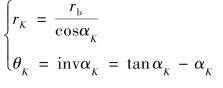
4.渐开线齿廓的啮合特点(www.xing528.com)

在传动过程中，要使一对齿从开始进入接触到脱开之前，下一对齿已进入接触，则必须使每对相接触的轮齿，在其接触点(线)K的公共法线方向，始终具有相同的速度，否则两轮齿在某瞬间就会脱开或嵌入，如图1-4-15所示。

动画1-34　齿轮啮合过程

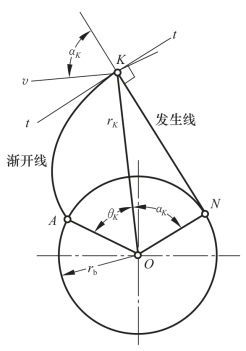
图1-4-14　渐开线的形成

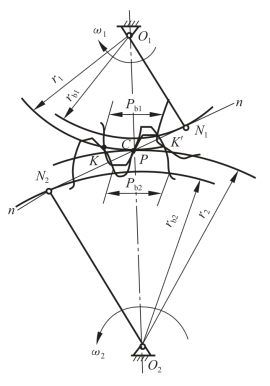
图1-4-15　渐开线齿廓的啮合特点

令两齿轮的角速度分别为ω1和ω2，从两齿轮轮心O1和O2分别作公共法线nn的垂线O1N1和O2N2，由几何关系可得两轮齿在接触点(线)沿公共法线nn方向的速度vn1和vn2分别为

vn1=ω1·O1N1，　vn2=ω2·O2N2

图1-4-16　各参数意义

同时由于公共法线nn与两轮的连心线O1O2相交于C点，则同样可由几何关系得出传动比，又可以表示为

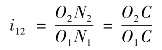
上式表明，一对齿轮的瞬时传动比等于其轮齿接触点处公法线所分连心线两段O1C与O2C的反比。

齿廓啮合的基本定律:不论两齿轮的齿廓在何位置接触，若其公法线nn皆通过连心线O1O2上的定点C，则传动比为定值。点C称为节点，以O1C和O2C为半径所做的两个相切的圆，称为两齿轮的节圆。

如图1-4-16设已知两渐开线齿轮的基圆半径分别为rb1和rb2，在两基圆上分别画渐开线C1和C2齿廓，它们在任意点K接触。过K点做两渐开线C1、C2的公法线nn，根据渐开线的特性可知，此法线为同时与两基圆相切。即此法线是两基圆的内公切线N1N2，它与连心线O1O2交于点C。又因两基圆均为确定的圆，O1、O2为确定的点，所以无论两齿廓在何处接触(如K点、C点等)，过其接触点的公法线均与公切线N1N2重合。因两个确定的圆在同一方向的内公切线只有一条，即N1N2为一确定的线。则它与连心线O1O2的交点C亦为确定的点，此点即节点。所以，渐开线齿轮能符合上述齿廓啮合基本定律，其传动比

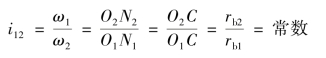
由上述可知，两渐开线齿廓接触点的轨迹为一直线，即两基圆内公切线N1N2。N1N2被称为啮合线。

如果过节点C作两节圆的公切线tt，则它与啮合点的齿廓公法线nn的夹角α′，称为啮合角。啮合角α′，在数值上就等于齿廓在节圆上的压力角α。

因此，渐开线齿廓的特点为:

(1)四线合一。啮合线、公法线、两基圆的内公切线、正压力的作用线，四线合一。

(2)渐开线齿廓啮合具有可分性。

动画1-35　啮合线为定直线

(3)渐开线齿廓啮合的啮合角不变。α′:N1N2与节圆公切线之间的夹角等于渐开线在节点处啮合的压力角。

(4)齿面的滑动。一对齿轮在节点啮合时，两节圆作纯滚动，齿面上无滑动存在，在任意点啮合时，由于两轮在啮合点的线速度不重和，必产生沿着齿面方向的相对滑动，造成齿面的磨损。