现代控制器设计方法-汽车工程手册：德国版

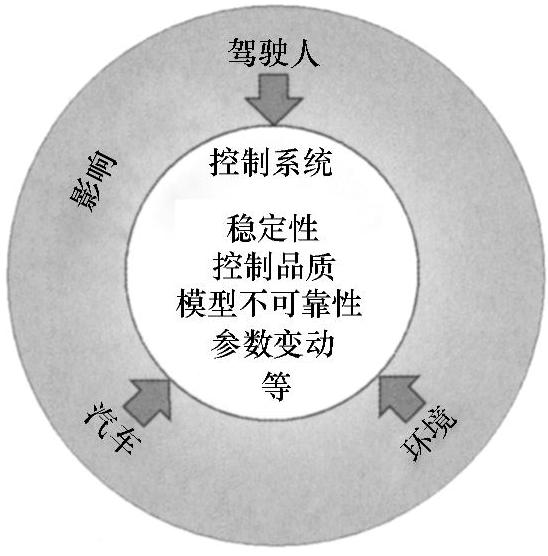
图8.8-1 在汽车环境下对现代控制方法的要求

汽车领域用得最广的PID控制^[4]包括最简单的、性价比非常吸引人的PID控制器。控制误差包括比例（P）、积分（I）、微分（D）三部分。这些误差的权重组合就是控制系统误差。许多使用者具有PID控制的基本知识，因为这些基本知识是很多工程定向培训教材的重要内容的一部分。在很多不了解模型知识的应用场合，利用参量的简单匹配或参量的自动化就可得到“可用的”控制器，但还不太可能得到“真正管用”的控制器。所以PID控制法在要求苛刻的应用场合还不能胜任。

下面将探讨在定向应用场合如何选择一些现代控制器设计的方法，这里没有一般性的说明，什么样的方法是优先选择的方法。因为每一种设计方法都有它的优点与缺点，它是与应用场合的具体要求综合权重的结果。

1.自适应控制

自适应控制可以控制模型不可靠的系统或动态变化的系统。自适应控制可以识别系统性能变化，并与变化了的新的系统性能匹配（图8.8-2）。自适应控制也可离线或在线实现。使用自适应控制系统的前提是要有在经典控制技术、非线性和数字系统以及系统识别方面的坚实知识。自适应控制器的衍生产品是自调节控制器，主要是PID控制器^[16]，它在工业上广泛使用，因为它可用旋钮（压钮）自行调节。常用的是“增益调配（Gain-Scheduling）“或参数调配（Parameter—Scheduling）”。不同工作点的控制参量是事先设计好的，在控制过程中自行转换。以模型为基础的高档自适应控制器，可以根据当前受控系统的性能连续跟踪参量的变化^[2]。在汽车领域它用于汽车底盘的自适应阻尼控制，以得到底盘的不同减振特性。

2.模糊控制

模糊控制运用现有有关过程控制知识，以语言表述形式和推理手段实现系统控制（Wenn-Dann-Regel）。图8.8-3表示在控制器中加入干扰。设计模糊控制不需要受控系统的数学模型，因而不需要线性化。如果控制器设计需要模拟，则就失去它的优点，因为为了模拟免不了需要受控系统的模型。采用简单的模糊设计方法可很快得到“可用的”控制器。较高档的模糊控制器由于所用的参数很多而较贵。好的模糊控制器设计离不开坚实的模糊控制理论。在现有有潜能的控制中，有缺陷的系统控制无法设计出性能优良的控制器，此外还不能识别相互矛盾的控制。在模拟控制器中可以将各种非线性参数组合在一起。经常是通过抓住复杂控制系统的本质可得到“真正管用的”控制器，但在设计时很难定量地做到这一点^[5]。模糊控制的示范性应用是模糊的ABS系统。在该系统中，原有的控制器和估计汽车重心速度都是利用模糊控制逻辑^[11]。

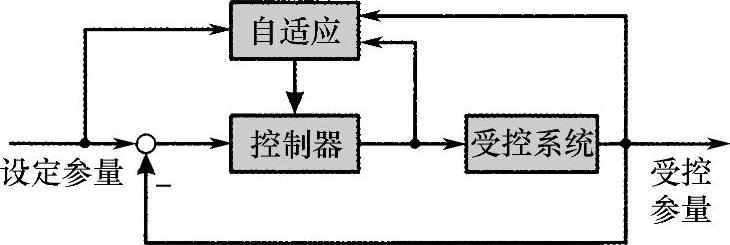
图8.8-2 自适应控制结构

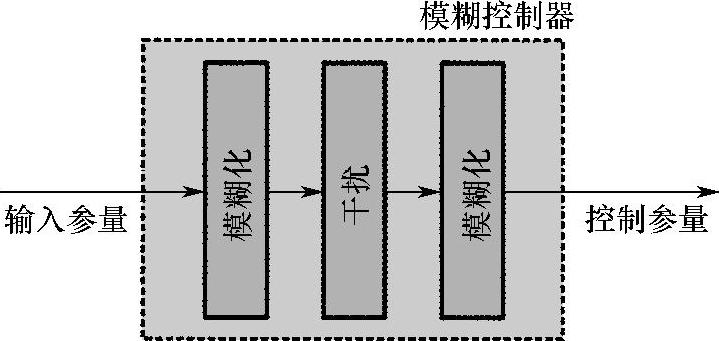
图8.8-3 模糊控制结构

3.Γ合成控制

Γ合成控制法作为持续开发经典的“极设定”设计，可以理解为在不可靠的受控系统上的扩展。总的闭环参考值的位置虽然有不可靠性，应限制在定义的极域上^[1]。Γ合成控制法主要限制在物理参数不可靠性的模型化上，即结构的不可靠性。不能再现的控制系统动态性能或简化模型不能通过非结构的不可靠性重新控制。像在进一步观察Γ合成的所有范围一样，由于闭环的多项式特征可得到控制系统的不可靠模型。利用聚焦优先安排有潜力的控制器，还可将时域和频域零位影响组合到控制器设计中，这样可以在整个经典的控制技术理论基础上设计控制器。Γ合成控制法有很多为控制器设计的辅助工具。当然也需要深入了解受控系统。

图8.8-4为控制器对极域的性能要求。时域要求如最小的动态激励时间或最小的阻尼时间。频域要求像限制频带宽度一样可以预先设定。由简单的几何元件组成的允许极域称为Γ域。如果带有不可靠性的闭环的所有特征值位于所希望的Γ域中，则可称Γ合成控制中的性能为真正管用的性能。因此，在设计前设计者要确定像希望的控制器结构这样的一些重要设定。Γ合成控制法以图形形式表明允许的系数范围，设计工程师可从中按自己的判断选择最好的系数。在宝马主动转向的稳定性功能中就使用了Γ合成控制法，目前已在产品3系、5系和6系上批量使用^[3]。

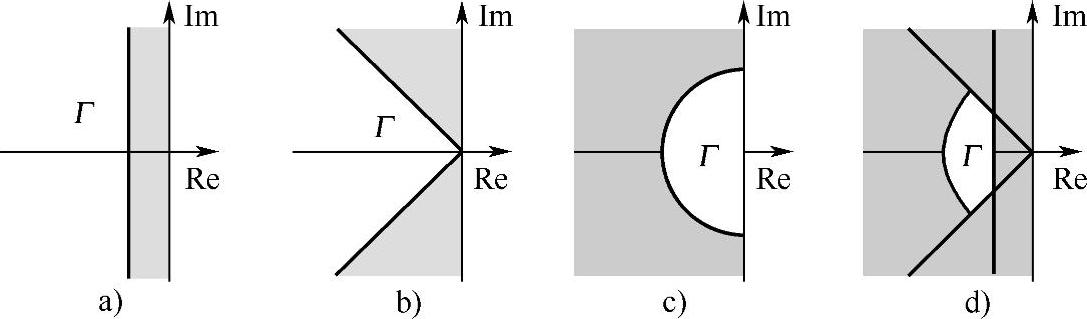
图8.8-4 说明控制器性能的极域

4.神经元控制

生物的神经系统是人工神经网络的范本。为完成一定的功能要训练神经元网络。由于神经元网络的这种性能，常用于自适应控制，重点是系统识别，部分也用于预测控制上^[13]。性能再现平台是将神经元控制和模糊控制结合起来，常常是在软件计算（Soft Computing）概念下将两者合并。对神经元控制，设计者必须就它的专门功能深入探讨并在系统识别方面具有坚实的理论知识，一般的控制工程知识则是次要的。因为神经元网络要训练后才能得到它本来的性能，所以需要很多的学习数据。在难于建模的情况下，可以采用控制系统的测量数据和为识别系统而将神经元网络作为学习数据。神经元网络还可用作模型随动（伺服）控制器。设计者通过设定的网络层面数量确定神经元网络的组合性（图8.8-5）。在神经元网络中由于它是黑盒子，没有给出它的透明结构。神经元网络的典型使用场合如发动机动态管理^[8]。

5.标准优化控制(www.xing528.com)

在标准优化控制中标准优化控制器设计方法是最年轻的一种设计方法。首先要定义控制工程问题的标准。这种设计方法将持续开发状态优化控制与优化的受控系统结合起来。H₂控制和H_∞控制法^[15]、μ合成控制法^[17]以及完全离散的、可解的L₁优化控制法^[14]均属于标准优化控制设计法。

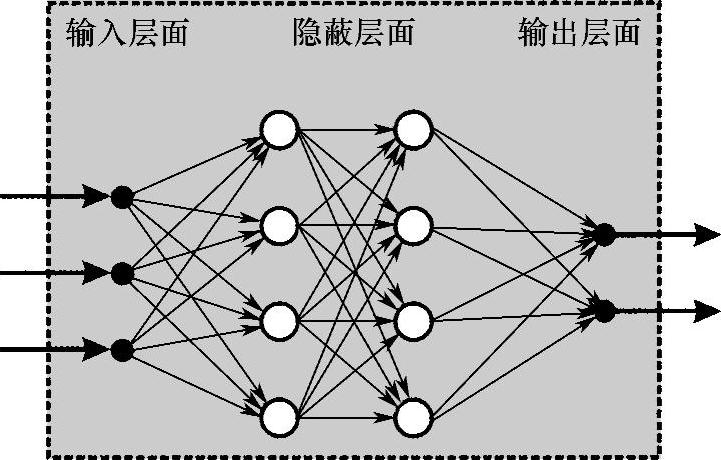
图8.8-5 神经元网络结构

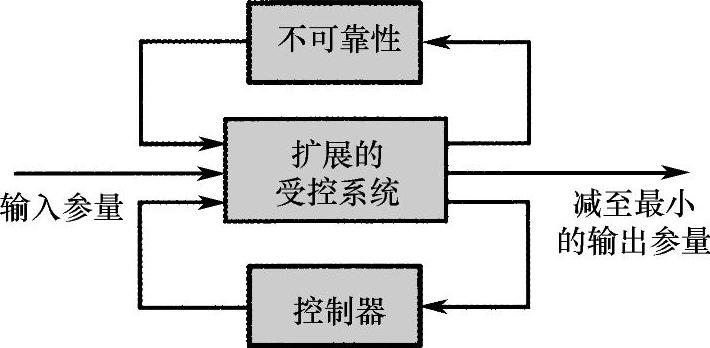
图8.8-6 标准优化控制结构

可能已有模型的不可靠性合成到控制器设计中（图8.8-6）。与频率有关的重要功能大多用于不可靠性的模型化。利用与频率有关的重要函数可以按频域调整百分数偏差（乘法不可靠性偏差），或由名义（不反映实际）的模型描述绝对偏差（加法不可靠性）。同样可以用重要函数来表达性能要求。最常用的、有3个重要函数的控制器结构是一种混合的灵敏度设计，这种设计可以有目的地实现与频率有关的控制特性模型化。在控制器合成时，可以将控制器的功能品质降至最小，由此可得到满足要求的优化的控制器。在接着的设计过程中不需要再分析，因为得到的控制器能确保所要求的、真正管用的控制特性。

因为控制器传递函数是自动迭代过程的结果，所以必须把控制器看成为黑盒子（不知道控制器有什么样的具体部件组成），并且不能透明地按部件组成实施控制。这样不存在事后再“人工优化”。标准优化控制器可能的应用场合是汽车车道引导辅助^[10]。

6.预测控制

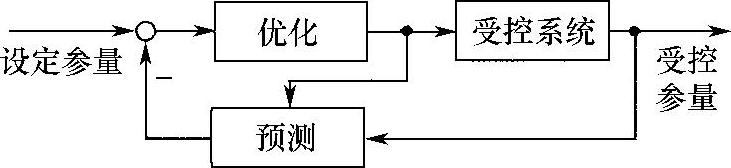
图8.8-7 预测控制结构

预测控制是这样的控制，它是在受控模型基础上的控制，它关注在定义的时间横坐标内未来受控系统的控制性能和根据优化控制情况组合到控制参数计算中（图8.8-7）。预测控制设计者需要数字控制的一般知识和控制品质准则。为设计预测控制，首先要集中时间建立精确的受控系统模型。第一批控制器设计相当简单，在设计较高档控制器时最大的困难在于要计算大量的参数。通过定义的品质准则，可以很好地实现从要求转换为预测控制法的算法（句法）。在预测控制器中不能保证系统的稳定性，为此要约束控制参数并可能放宽非线性过程^[12]。预测控制用于汽车横摆控制，以及时制止汽车的过度转向或不足转向。

7.定量反馈理论（QFT）

真正管用的、按定量反馈理论（QFT-Quantitative Feedback Theory）设计的控制是频域中的一种方法，在宽广的系统特性上使用：时间不变和时间可变，线性和非线性，连续和时间离散，单参数系统和多参数系统^[15]。QFT的组合目标是设计尽可能低频率阶和最小频带宽度的控制器，纵使受控系统具有不可靠性，但仍要保证控制器的优良的、稳定的控制性能。重要的是利用定向频域有针对性地表示系统的不可靠性和性能要求，要一直贯穿到整个设计过程中。尼科尔斯（Nichols）图作为图形的辅助工具，它的优点是将伯特（Bode）图与极表示结合在一起。控制器结构的不可靠性可以用进入传递函数中的参数间隔时间确定。控制器非结构的不可靠性最简单的方法可以以相同的型式和方式予以说明，或在说明性能要求时将控制器非结构的不可靠性组合到设计中。

为说明性能要求，可为设计者提供一个宽广的系统特性：在偏差很窄的时域中和在约束函数的频域中，可以说明对控制系统出现的每一个传递函数的各个要求（图8.8-8）。对闭环控制的性能要求可以特别灵活地、非常针对性地带入到设计中。

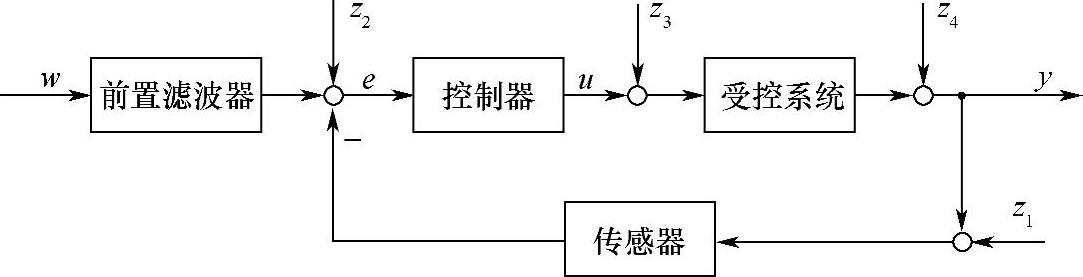
图8.8-8 为QFT设计的控制回路结构

w—设定参量 y—受控参量 z₁～z₄—干扰参量 e—控制偏差 u—控制参量

设计过程在于通过有针对性地补充控制器元件改变控制器频率变化的相位和大小，使在整个定义的边界曲线内不牺牲性能要求。在整形电路（Loop Shaping）中为设计者提供已知的所有传递函数的元素。到底在控制器中有多少传递函数的元素才能满足要求，主要取决于设计工程师的诀窍（Know-How）。利用经典控制工程中的丰富经验可以以简单的型式和方式得到低频率阶和最小的频带宽度的真正管用的控制器。在经验很少时存在这样的风险，即由于附加很多传递函数的元素得到高频率阶的控制器。按QFT设计的控制器性能在乘用车车道自动引导中得到很好验证^[7]。