汽车工程手册：德国版-发动机类型及结构

1.往复活塞式发动机

（1）结构型式　在汽车制造业中见到的发动机结构型式有直列、V形、对置和少数还有W形的发动机（图5.1-4）。在V形发动机中还有亚属VR形发动机，它的两个气缸排的V形夹角很小，并安装一个共同的气缸盖。单缸和双缸发动机一般只用在摩托车上。乘用车领域采用3气缸、4气缸、5气缸、6气缸、8气缸、10气缸、12气缸的发动机。在个别情况下和样机上，也有V形、V—VR形、W形的16缸或18缸发动机。

计算气缸数的方向按汽车发动机的DIN73021标准（船用和通用发动机按ISO 1204、1205标准，计算气缸数方向则相反，从曲轴输出端看）。从与曲轴输出端（飞轮）对面对气缸连续编号。在多气缸排发动机中，首先计算曲轴轴线左侧的气缸排的气缸数，接着计算绕发动机曲轴轴线顺时针旋转方向的下一个气缸排的气缸数。

点火（着火）顺序是发动机各气缸相互点火（着火）的次序。点火（着火）顺序由发动机结构形式、追求相同的点火（着火）间隔、可生产的曲轴形状、较低的曲轴应力等因素决定。点火（着火）顺序从第1缸开始。

直列发动机（图5.1-4中1）可采用多达6缸的型式，每个气缸有一个曲轴曲拐，通常为整体气缸盖。对置发动机（图5.1-4中4）气缸排相对180°，每个气缸也有一个曲拐，每个气缸排用一个整体气缸盖。

V形发动机（图5.1-4中2）的特点是一个曲拐驱动每一气缸排的一个连杆（即两个连杆），每个气缸排共用一个整体气缸盖，两气缸排的角度成60°、72°或90°。V形夹角由气缸数（均匀的点火或着火顺序）或不同缸数的发动机系列的主流发动机气缸数决定。图5.1-4中的3是特殊的发动机，它的V形夹角靠近到15°。这样，两气缸排只要一个整体气缸盖，而每个气缸有它自己的曲拐，所以也称“直列发动机”，并按相应的直列发动机确定点火（着火）顺序。开始也将这种发动机称为VR发动机，因为它的结构型式不像直列或V形发动机明了、直截了当。值得一提的是这种发动机的曲轴是错拐曲轴。通过奇数气缸1、3、…和2、4、…的两个平面相交线位于曲轴轴线下面。这样第1、3、…气缸从上止点（OT）到下止点（UT）的角度距离稍小于180°KW（曲轴转角），而第2、4、…气缸从OT到UT的角度距离稍大于180°KW。

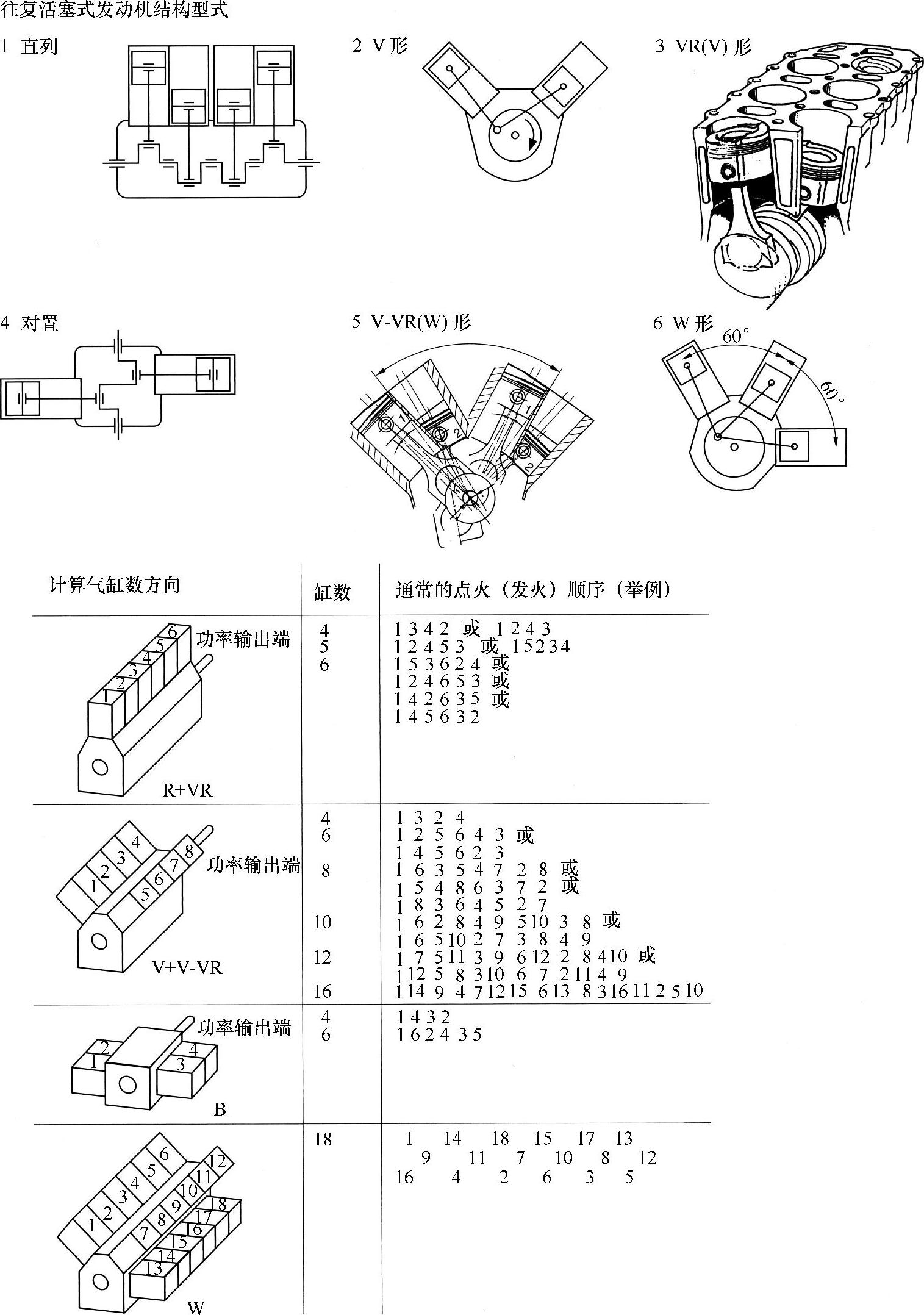
图5.1-4 汽车发动机结构型式、计算气缸方向和点火（发火）顺序

VR发动机其他变型为V-VR发动机（图5.1-4中5）。在此基础上还采用W形发动机。每台VR发动机气缸排的两个连杆共用一个曲拐。点火（着火）顺序按两个VR发动机气缸排的V形发动机点火（着火）顺序给定。

图5.1-4中的6称为W形发动机。它有3个气缸排，每排60°夹角，最多可达3×6=18个气缸。每个曲拐上有3个连杆。这种型式的发动机主要优点是在有很多气缸时，发动机纵向尺寸十分紧凑，工作非常均匀，振动很低。

当大量乘用车采用4缸发动机、工作容积为1.2～2.0L时，在舒适型和豪华型乘用车领域不断采用6、8、12缸发动机。在紧凑型和准紧凑型乘用车领域出现小型4缸发动机或3缸发动机。3缸发动机是在现有4缸发动机系列基础上派生而来，它在这种汽车的市场份额中具有较低的开发、生产成本的优势。

（2）曲柄连杆机构运动学 曲柄连杆机构将燃烧产生的气体作用力通过活塞往复运动转换成曲轴转动和有用转矩^{[5，6，7，8]}。由曲柄连杆机构的几何学（图5.1-5）可推导出活塞行程s_k在连杆比λ=r/l时随上止点开始的曲轴转角α的变化：

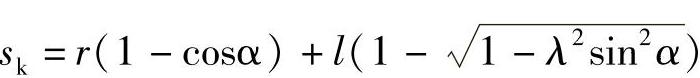
近似计算公式为：

s_k≈r（1-cosα+λ/2·sin²α）

由此得到活塞速度

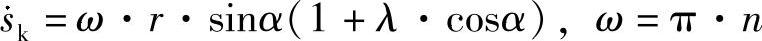
和活塞加速度

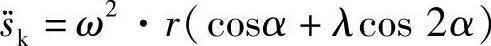
图5.1-5是活塞加速度随曲轴转角α和在不同连杆比λ时随活塞行程s_k的变化。在λ=0时，即连杆无限长，活塞位移、速度、加速度为纯正弦变化。

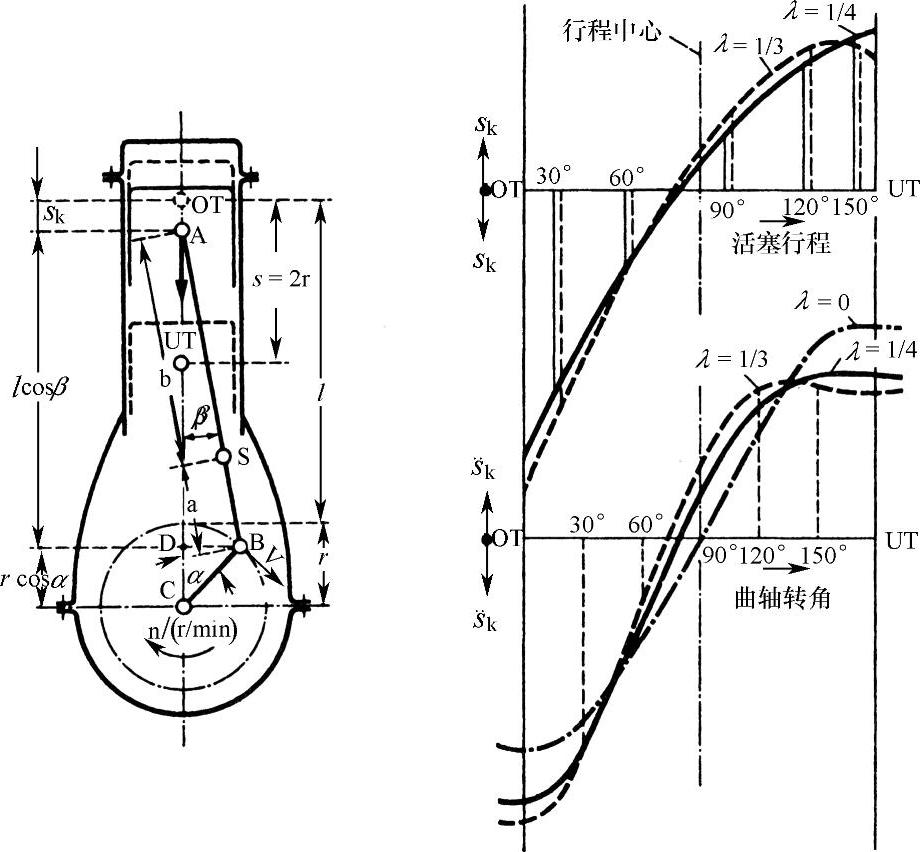
图5.1-5 曲柄连杆机构往复质量的几何学和加速度

（3）曲柄连杆机构中的各种力和力矩　除气体作用力外，在曲柄连杆机构上由于往复活塞式发动机的周期性工作循环和不均匀的运动方式，还有惯性力的作用。既有“内力”，也有“外力”。为计算活塞、连杆曲轴和支架，需要确定内力。自由的“外力”引起发动机的力和力矩并使发动机振动。这些力和力矩必须由发动机支架吸收并按力的传递路径传到汽车构件上。

由加速度可以得到气缸中心线方向的往复惯性力：

F_m=m_h·r·ω²·（cosα+λcos2α）

往复质量的近似计算公式为

m_h≈1/3·m_s+m_k

式中，m_s为连杆质量；m_k为活塞质量。

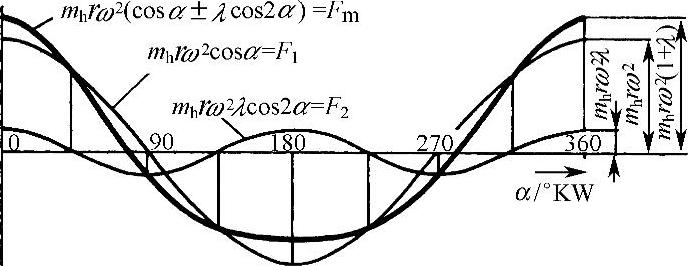
如果将cosα和cos2α随曲轴转角变化的值代入往复惯性力的公式中，就可用图清晰地表示往复惯性力F_M随曲轴转角α的变化（图5.1-6）。α是正弦变化的1阶惯性力和曲轴每转中带有两个完全振动的2阶惯性力的叠加。在上止点时合力要高于其中的任一个力，而在下止点时合力的绝对值要小于1阶惯性力的绝对值。

转动质量的近似值为：

(www.xing528.com)

图5.1-6 往复惯性力分为基波和谐波

m_r≈2/3·m_s+m_kur

式中，m_kur为没有平衡重平衡、与连杆轴颈中心有关的曲轴转动质量。

这样就可按公式计算离心力：

F_r=m_r·r·ω²

往复惯性力F_M和离心力F_r分别随质量m_h和m_r线性增加，随角速度ω呈平方增加。研究曲柄连杆机构运动学的目标是曲柄连杆机构的活塞、活塞销、连杆尽可能做得轻和连杆比λ尽可能小，也就是采用长的连杆。

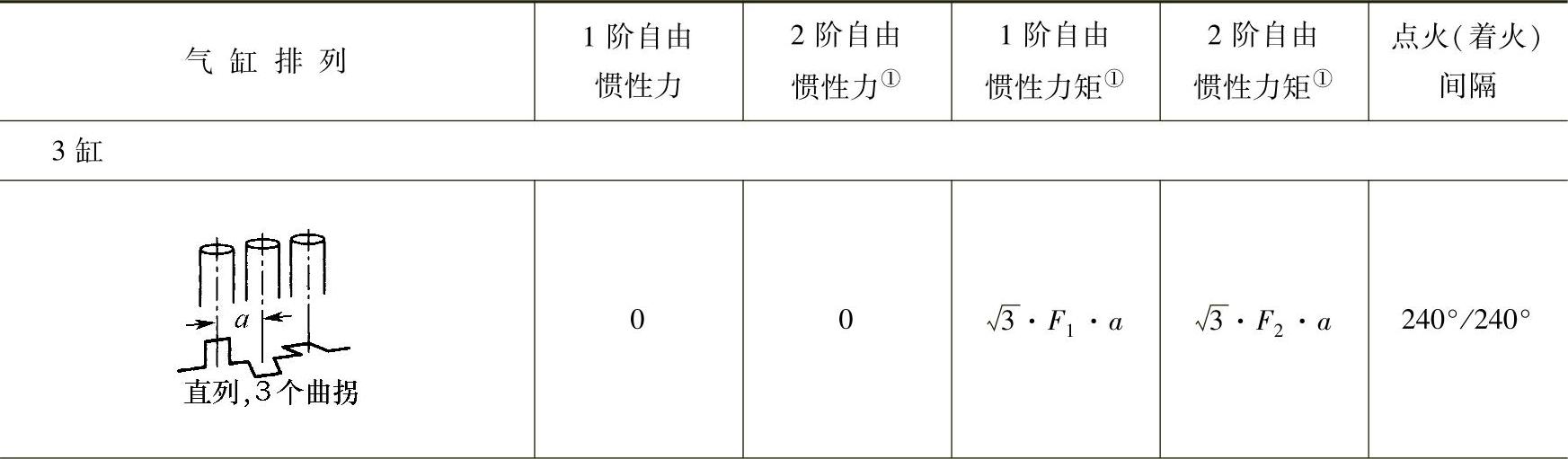
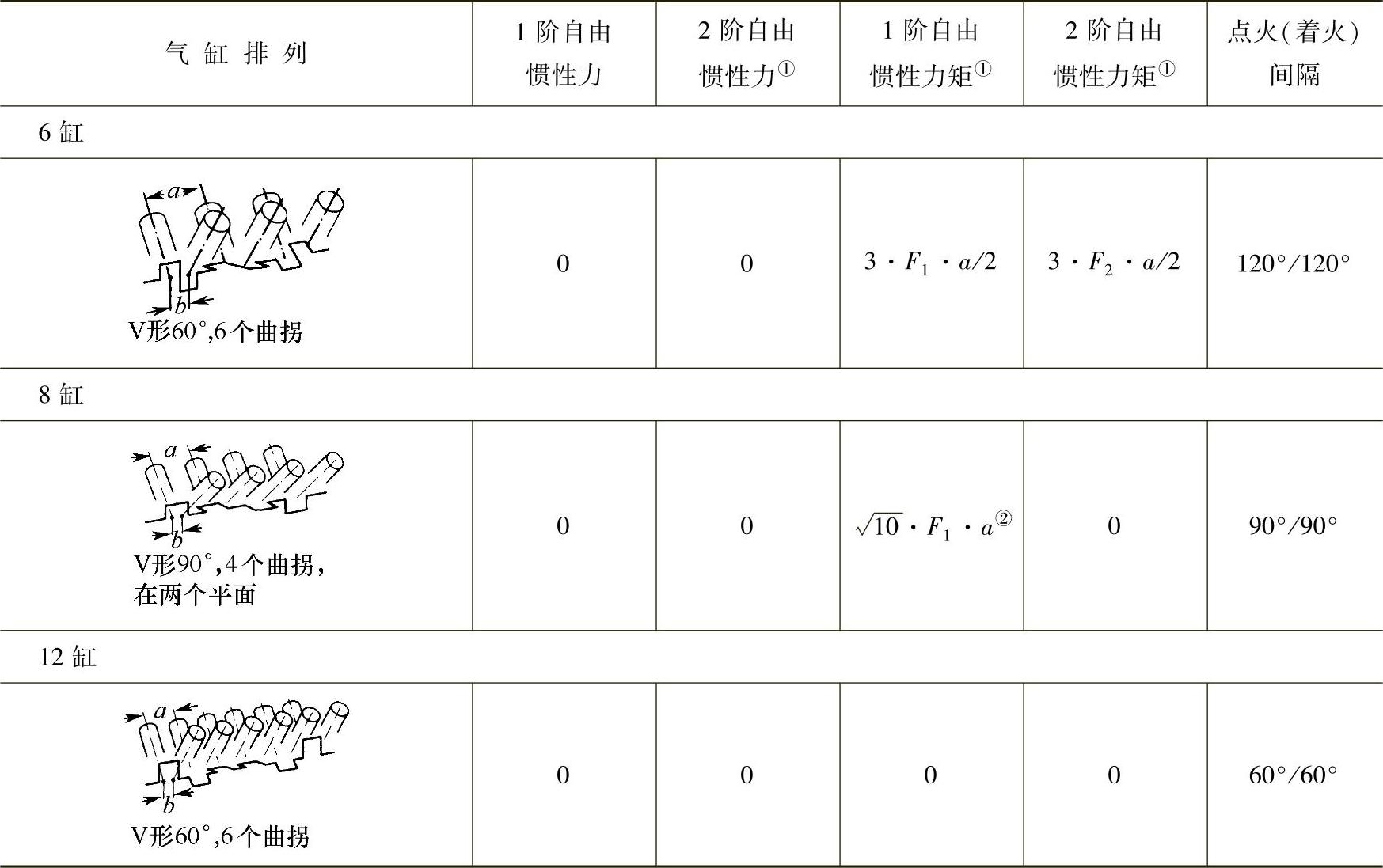
在多缸发动机中，每个气缸的活塞往复惯性力叠加，并可部分地抵消。在发动机纵向，这些惯性力作用在各气缸中心线相互间隔（缸心距）的平面上，并产生惯性力矩。按气缸排列和曲轴结构型式，这些惯性力和惯性力矩使外力和外力矩增加，但也相互抵消向外的力。这就是人们所说的发动机“自由”惯性力和“自由”惯性力矩。表5.1-1是流行的一些发动机结构型式和它们的1阶、2阶自由惯性力和自由惯性力矩。

表5.1-1 一些常用发动机型式的1阶、2阶自由惯性力和自由惯性力矩（没有平衡措施）

（续）

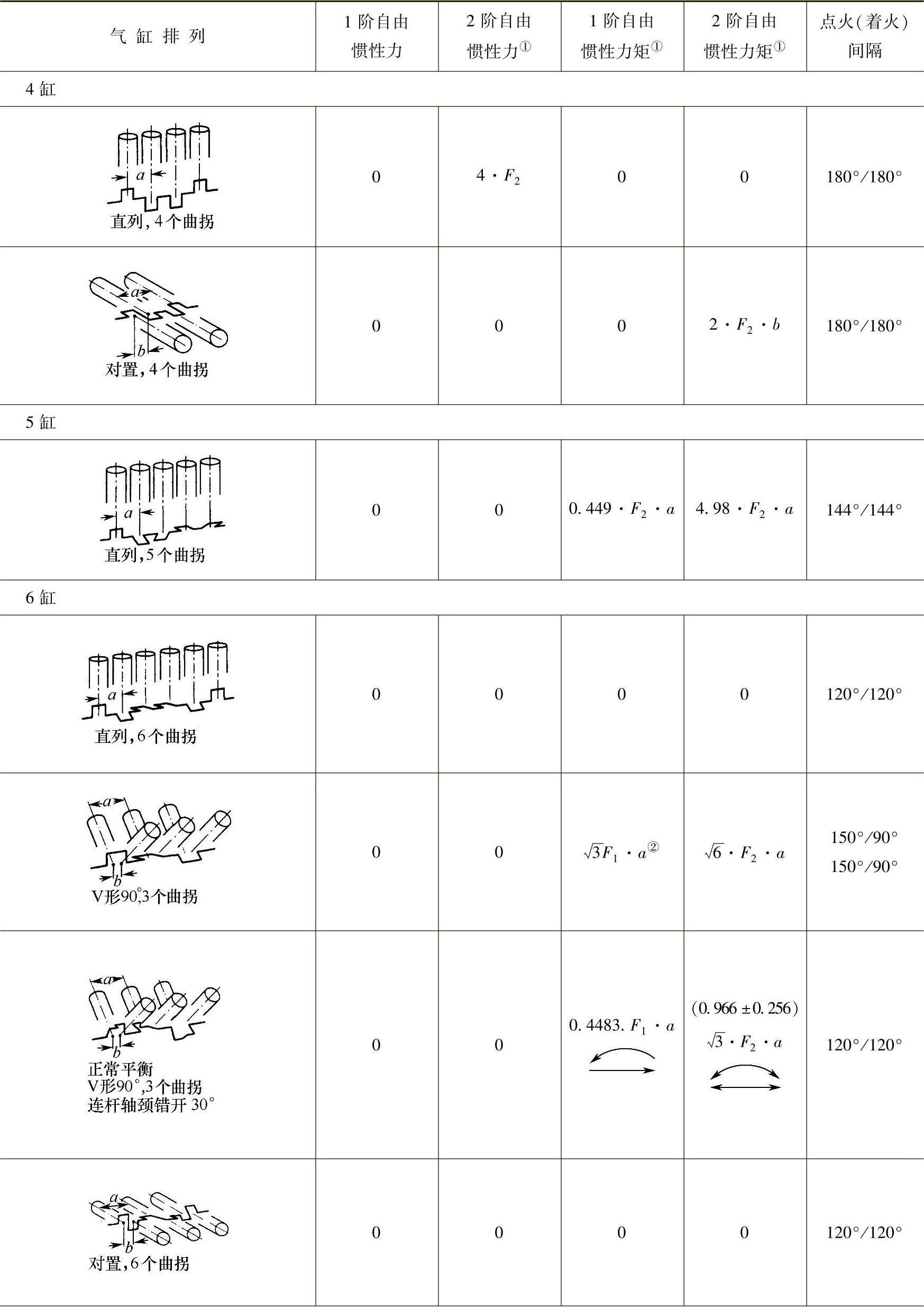
（续）

① 没有平衡重。

② 利用平衡重全平衡。

作用在活塞上的气体力F_G可分解为作用在连杆上的连杆力F_SG和作用在气缸壁上的侧向力N_G（图5.1-7）。连杆力F_SG在曲轴曲拐上又分解为作用在曲轴曲拐（连杆轴颈）上的径向力F_RG和切向力F_TG。作用在曲轴曲拐上的切向力，即曲轴半径为r的切向力F_TG形成使曲轴转动的力矩r·F_TG。根据曲轴转角α、连杆摆动角度β和连杆比λ，就可以与推导惯性力类似的方法推导并计算这些力。

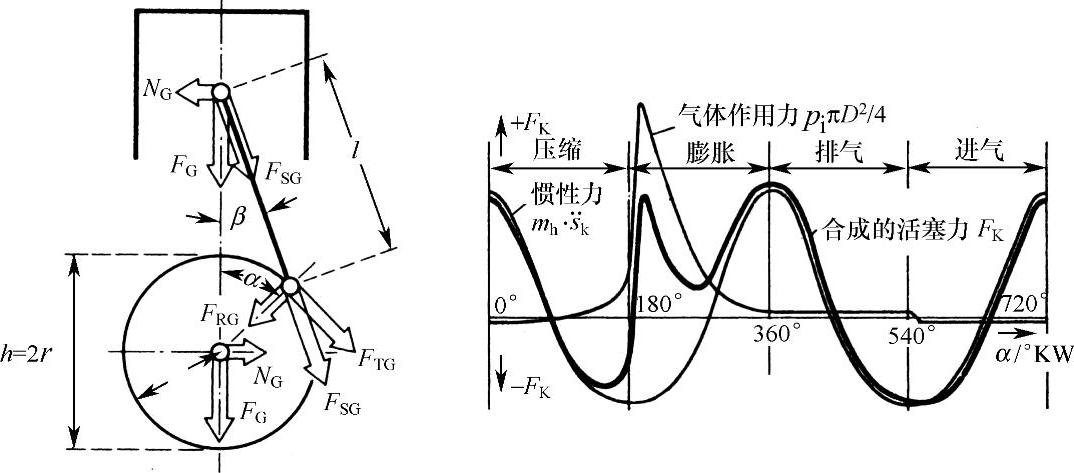
图5.1-7 气体作用力分解和惯性力与气体作用力合成的活塞力F_K

如果将作用在活塞上周期变化的气体力和曲柄连杆机构中往复运动部分的周期性变化的往复质量惯性力汇集在一起，就可得到合成的活塞力F_K随曲轴转角α的变化关系。图5.1-7定性地表示活塞力F_K的变化趋势。气体力的大小随发动机负荷近似线性变化。惯性力随发动机转速呈平方增加。因此，在低转速、全负荷时气体力是主要的，在高转速时惯性力是主要的。

曲轴上各曲拐相互错开的多缸发动机，在发动机工作时各个离心力叠加。由此得到如图5.1-8表示的各种发动机结构型式在720°KW（曲轴转角）的一个循环中离心力F_T的变化过程。离心力的变化激励曲轴的扭转振动，它主要影响曲轴的疲劳强度。气缸数越多，作用在曲轴上的离心力的不均匀性越小，越接近平均离心力F_Tm。在一个工作循环剩余的离心力波动引起曲轴端部（自由端）的不均匀的扭转振动，可用不均匀度表示，其定义为：

δ_S=（ω_max-ω_min）/ω_min

不均匀度可利用飞轮的惯性予以减小。飞轮尺寸（飞轮的惯性）多大合适需要具体确定，要兼顾转动的不均匀性与瞬时的加速性能/高速行驶性能。

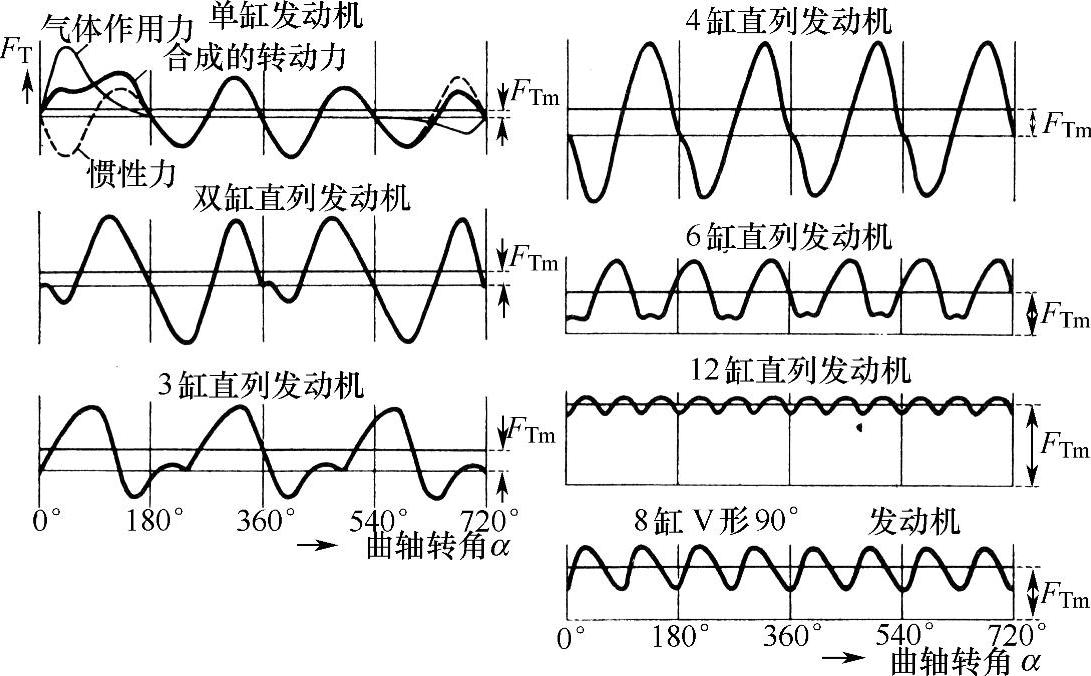
图5.1-8 各种发动机结构型式的离心力F_T的变化过程

自由力和自由力矩可以利用随曲轴一起转动的平衡质量（1阶）或2倍于曲轴转速的离心质量（2阶）完全或部分抵消。这样，发动机支架不必或很少承受来自曲柄连杆机构运动质量产生的各种力。设计发动机和变速器支架时，集中于支撑来自发动机-变速器总成输出力矩的作用力和来自汽车行驶在纵向、垂直、横向加速时整个动力装置惯性的作用力。

2.转子活塞式发动机

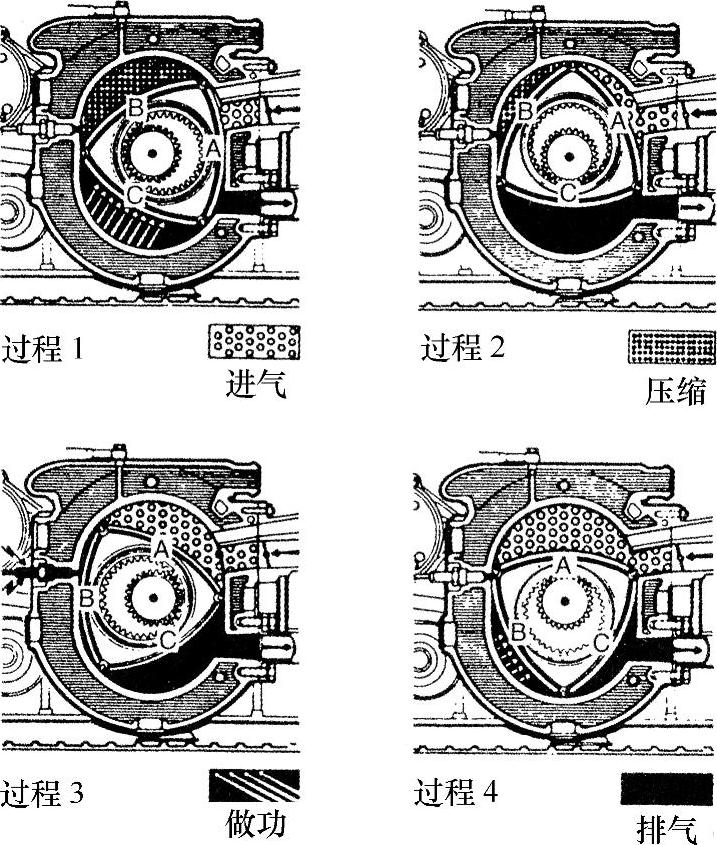
图5.1-9 汪克尔发动机（Wankelmotor）原理

转子活塞式动力装置有一台齿数比为2∶3的转子活塞式发动机，并以大家熟知的汪克尔发动机（Wankelmotor）命名，并在发动机制造业中得到实际应用（图5.1-9）。它的优点是运动质量完全平衡，其效果是运转轻声，结构紧凑，没有配气机构。其主要缺点是窄长的、不利的表面/体积比的燃烧室，导致淬火效应和高的HC排放；燃油、机油消耗高。马自达公司在NSU（Wankel Spider，1964和RO 80，1967）首批成功使用后，仍不断呵护这些型号和详细改进，为马自达品牌的技术形象赢得好的声誉。最新的转子发动机Renesis见参考文献[9]。