动力电池系统故障分析与应用

1.应用背景

随着新能源汽车产业的发展，纯电动汽车的安全问题和质量问题已经成为人们关注的热点。动力电池系统作为纯电动汽车中重要的能源存储装置，在其使用过程中发挥着重要的作用。近年来频发的动力电池系统危险故障加剧了纯电动汽车消费者的担忧，因此加快动力电池系统的故障诊断和安全管理势在必行。对动力电池系统进行故障诊断，明确故障类型，定位故障位置，避免故障发生，对电动汽车的稳定性提升有十分积极的作用。

本案例通过纯电动汽车运行大数据的统计分析，研究动力电池电压的变化规律和异常波动，并据此判定故障概率，最后与实车对应，将数据统计故障诊断结论转换成实际车辆故障诊断结论。

2.处理流程

3σ多层次数据筛选的主要作用是运用高斯分布的概率特性，对无故障数据进行集中筛选。多层次数据筛选策略运用3σ准则进行筛选。图5-3所示为高斯分布中心值附近不同分布区间内的概率密度，从图中可以看出在3σ之外的概率之和只有不到0.3%，因此事件发生在3σ范围之外的概率非常小。在多层次筛选算法中，给定一组中心值应该一致的数据，认为超过3σ范围的数据存在故障。在建立高斯分布时，高斯分布的中心位置应该减少这些故障数据的影响。因此在多层次筛选算法中，每一次筛选都会将数据组中超过3σ范围的数据剔除掉，并重新计算中心值。

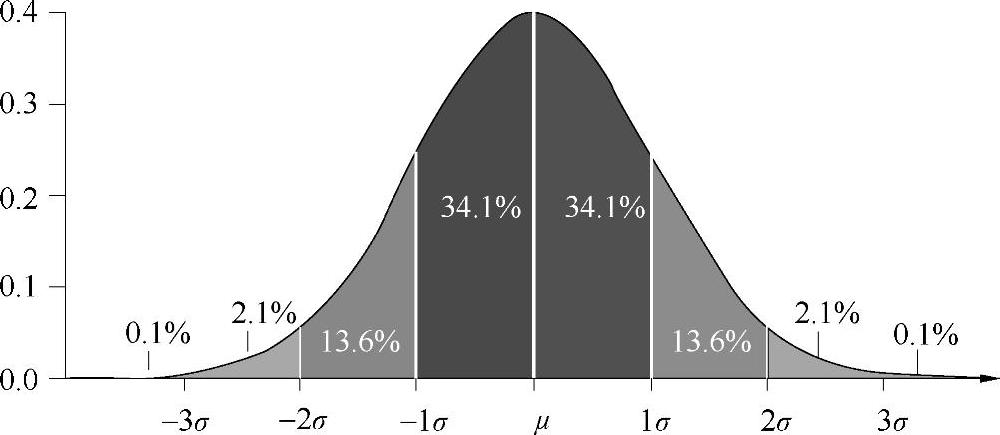
图5-3 不同σ区域概率密度分布

下面以北京某车型样车在2016年某日行驶的行向量（物理意义为电池单体端电压）为例，对多层次3σ筛选过程进行解释计算。电池组中有91个单体，电压形成行向量D1。

D1=[4.024.024.024.024.024.0944.024.0244.024.024.024.024.024.02 4.024.0244.024.0244.024.024.024.024.024.02444.024.024.024.024.024.02 4.0244.024.024.14.024.024.024.024.024.024.0244.024.024.024.024.024.02 4.024.024.024.024.024.024.024.024.024.024.0244.024.024.024.024.024.02 4.024.024.0244.024.024.024.024.024.024.024.024.024.024.024.024.024.02]

从图5-4可以看到，在第6位置和第41位置电压值明显超出电池组电压平均水平，计算这组端电压的均值时不希望被这两个位置影响。因此在计算均值时，利用多层次筛选算法将这两个值剔除出去。

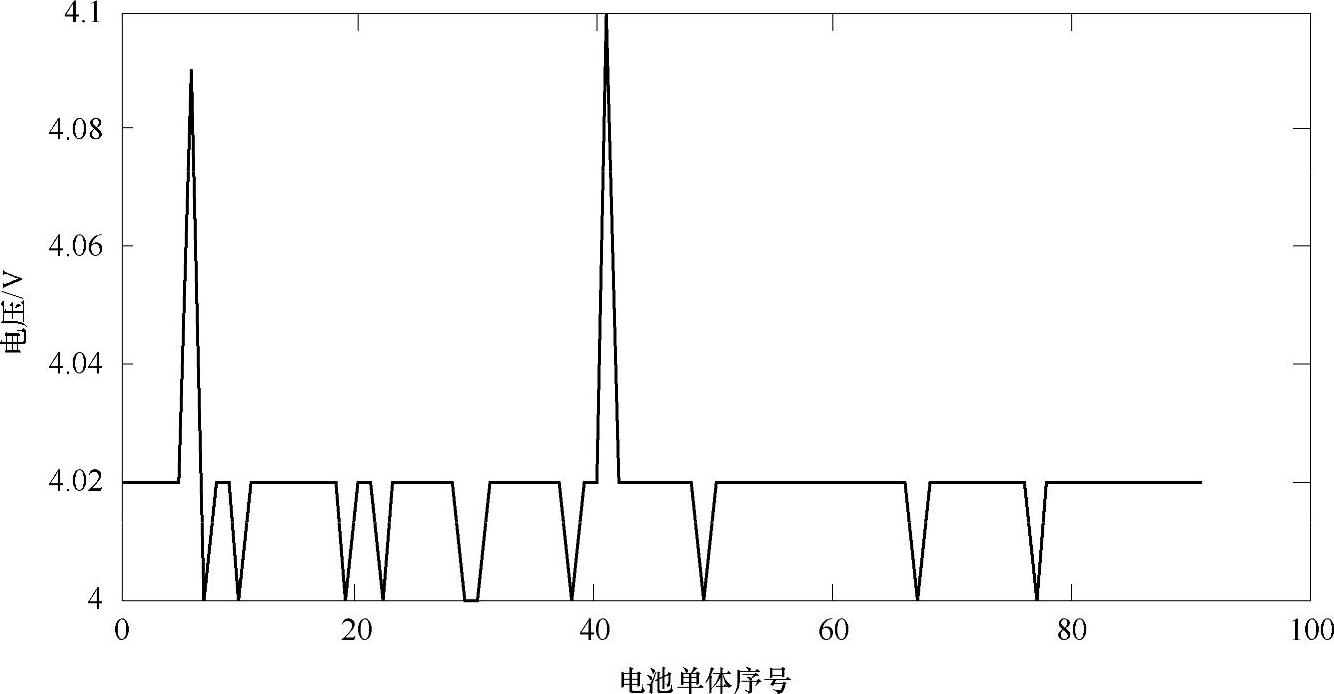
图5-4 D1端电压

从图5-5中可以看到这组电池数据的中心在4.0195附近，标准差为0.0130。

mean（D1）=4.0195 （5-1）

std（D1）=0.0130 （5-2）

高斯分布如图5-5所示。

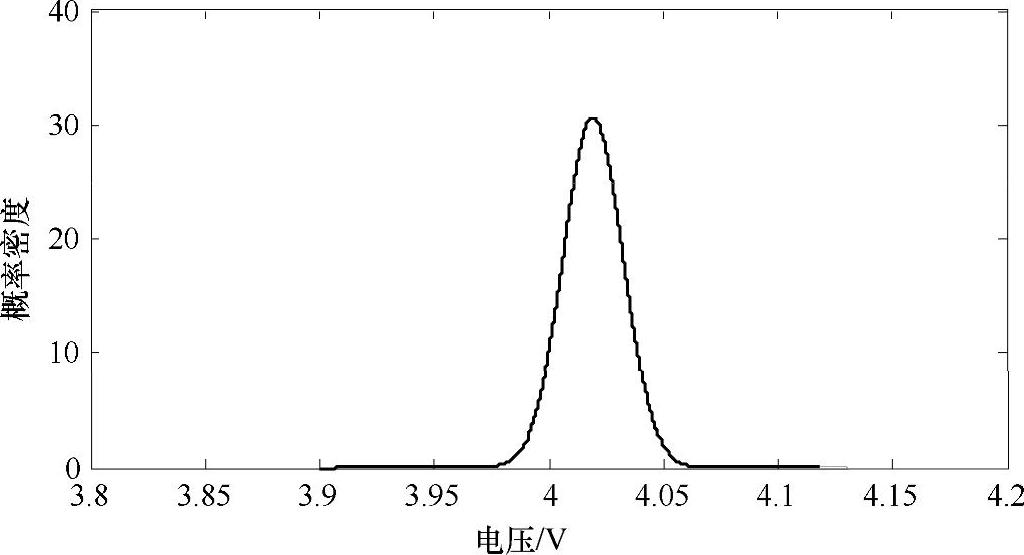
图5-5 D1行向量高斯分布

根据多层次数据筛选算法，认为故障值在（μ-3σ，μ+3σ）区间之外，计算上下限为

μ+3σ：4.0195+3×0.0130=4.0585 （5-3）

μ-3σ：4.0195-3×0.0130=3.9805 （5-4）

3σ范围为

（3.9805，4.0585） （5-5）

第4位置和第41位置偏离值为

D1（6）=4.09 （5-6）

D1（41）=4.1 （5-7）

经过3σ第2层筛选，发现第6个数据和第41个数据超出3σ范围，筛除这两个数据，再用另一个矩阵D2记录其他数据，即

D2（41）=[ ] （5-8）

D2（6）=[ ] （5-9）

重新计算均值和标准差：

mean（D2）=4.0178 （5-10）

std（D2）=0.0064 （5-11）

用筛选过的数据D2重新建立高斯分布，从图5-6中可以明显看到高斯分布向中心值收紧。从标准差可以看出去掉个别超出3σ范围的数据后，标准差下降到原来的49.2%。

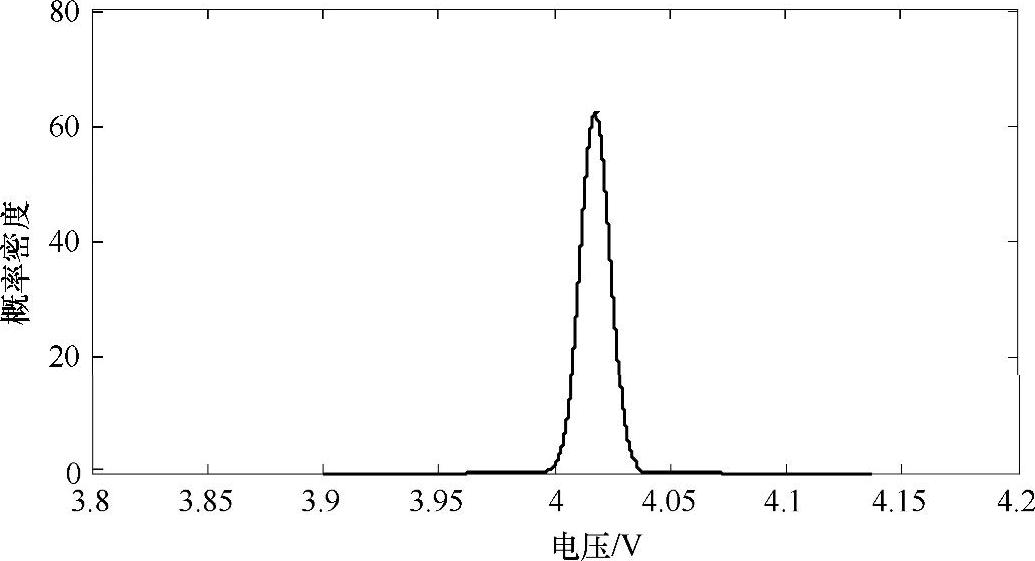
图5-6 D2高斯分布

从图5-7可以看出，经过一次3σ筛选计算后，第二层的数据与第一层的数据中心值存在一个差值（图5-5中绿色直线在x方向投影），这个差值就代表了一次筛选后对原来中心值进行的调整。从原始D1数据可以看到，大部分数据都落在4.00～4.02，因此均值约为4.01；但因为第6和第41数据异常偏大，导致均值偏离到4.019，所以去掉个别超出3σ范围的数据后得到的中心值将更能反映该无故障系统整体的中心位置。这样做的目的是为了在下一步的研究中更能反映无故障系统整体的高斯分布，来定位故障或异常在高斯分布中的位置及置信水平。

多层次3σ筛选算法的优点：一是这种方法一次筛选能同时去除所有超过3σ置信区间的数据，处理效率高；二是这种方法能按照置信区间来调整阈值。为后期车辆数目、车辆种类、不同时间等多维度的大数据处理，提供了高效的算法。在后期也大大地节省了运算的时间，提高了运算的效率。

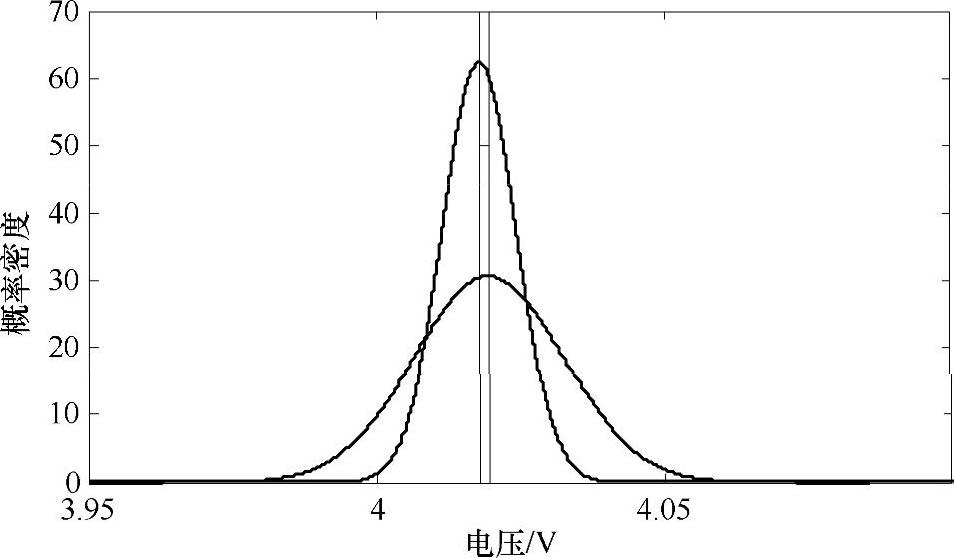
图5-7 两次高斯分布距离

为了后期对电池组组内电池单体之间故障规律进行预处理，该算法用故障矩阵R将超过3σ的数据位置保存。在实际中经过计算，发现一次筛选后，第二次的中心值就足够精确，因此将程序直接编写为两次筛选，提升了计算速度，简化了程序。电池系统单体端电压故障诊断模型是根据得到的端电压数据形式并结合统计学算法进行建立的，其算法流程如图5-8所示。

其中过程1到2为故障判定核心处理算法，其流程如下：

①根据某时刻采集到的电动汽车电池单体实时端电压数据，建立端电压数据矩阵：

U_t^（0）=（U_t，1^（0），…，U_t，n^（0）） （5-12）

进行高斯分布建立计算：

U_t^（0）～（μ_t0，σ_t0） （5-13）

②去除3σ范围之外的端电压数据，并建立新的数据矩阵：

U_t^（1）=（U_t，1^（1），…，U_t，n^（1）） （5-14）

再次进行高斯分布建立计算：

U^（1）_t～（μ_t1，σ_t1） （5-15）

③重复步骤②，对数据进行m次过滤得到最终理想分布：

U_t^（m）～（μ_tm，σ_tm） （5-16）

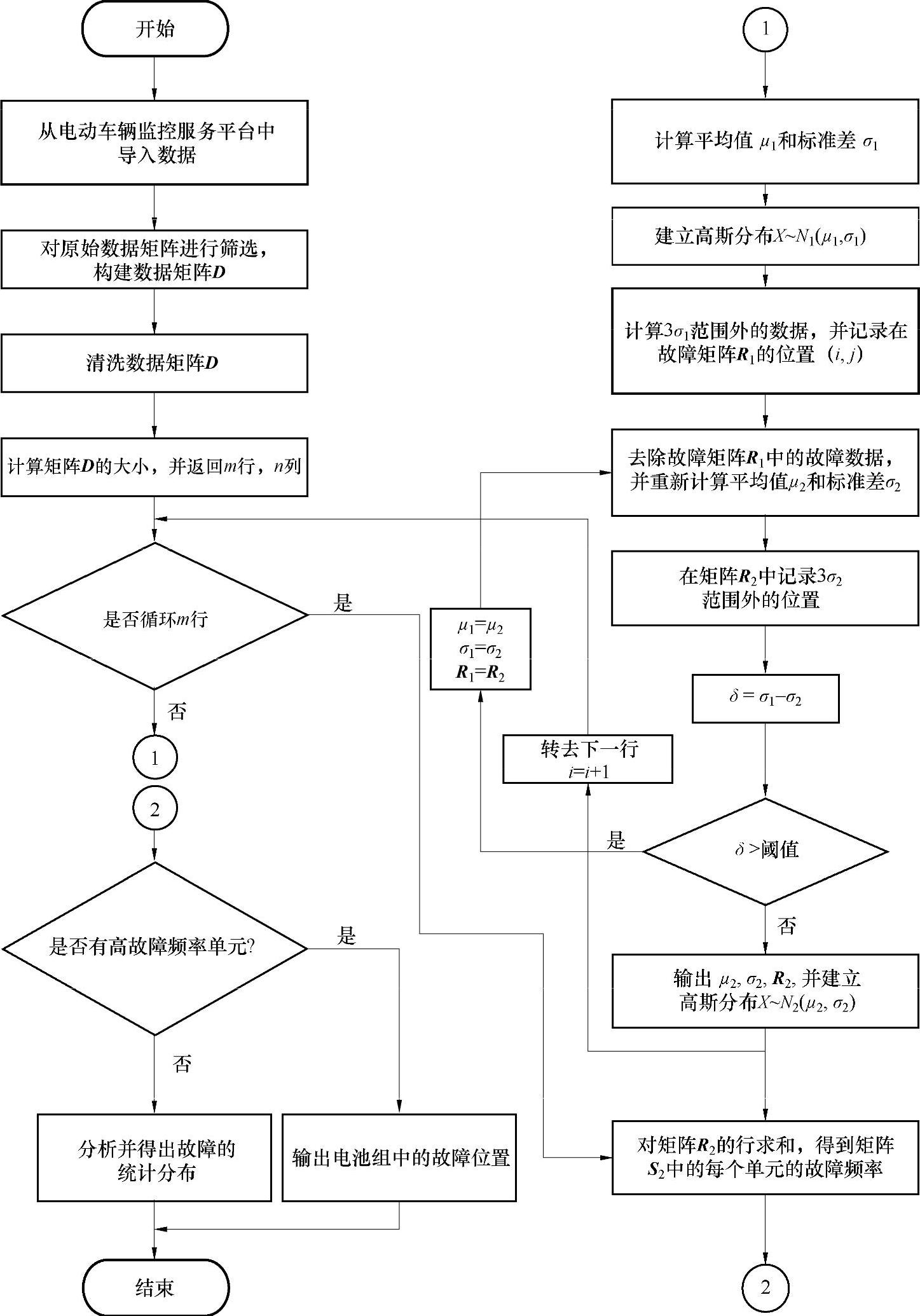
图5-8 电池系统单体端电压故障诊断模型(www.xing528.com)

④设定参考故障诊断范围（μ_tm+β·σ_tm），对得到的最终分布进行比较判断，其中β是可调节阈值。在故障诊断矩阵R_t中，把故障诊断范围外的数据设为1，故障诊断范围之内的数据设为0，建立t时刻的故障诊断矩阵R_t为

R_t=（R_t，1，…，R_t，n） （5-17）

在这里，R_t，i=0或1。

⑤选定一个时间段（t₀～t₁），进行从步骤①～步骤④的循环计算，得到这个时间段内的故障矩阵：

R_t=（R_t，1^T，…，R_t，n^T） （5-18）

3.处理结果

（1）两种类型的故障定义

对大量同种车型车辆进行故障诊断，通过对这些车辆的大数据结果整合分析，在这里定义两种故障：

①对于小部分车辆，某个不确定位置的电池单体电压经常超3σ范围，并且它们的故障频率通常超过90%。定义这种故障为偶然故障，原因为某些偶然的问题（如生产问题、意外情况）导致的该单体故障概率比较大，如图5-9a所示。

②对于大部分车辆，有一个或几个固定位置的电池单体，它们的故障频率低于35%，如图5-9b、c、d所示。这种故障的原因主要是设计缺陷和一些固有的系统问题。

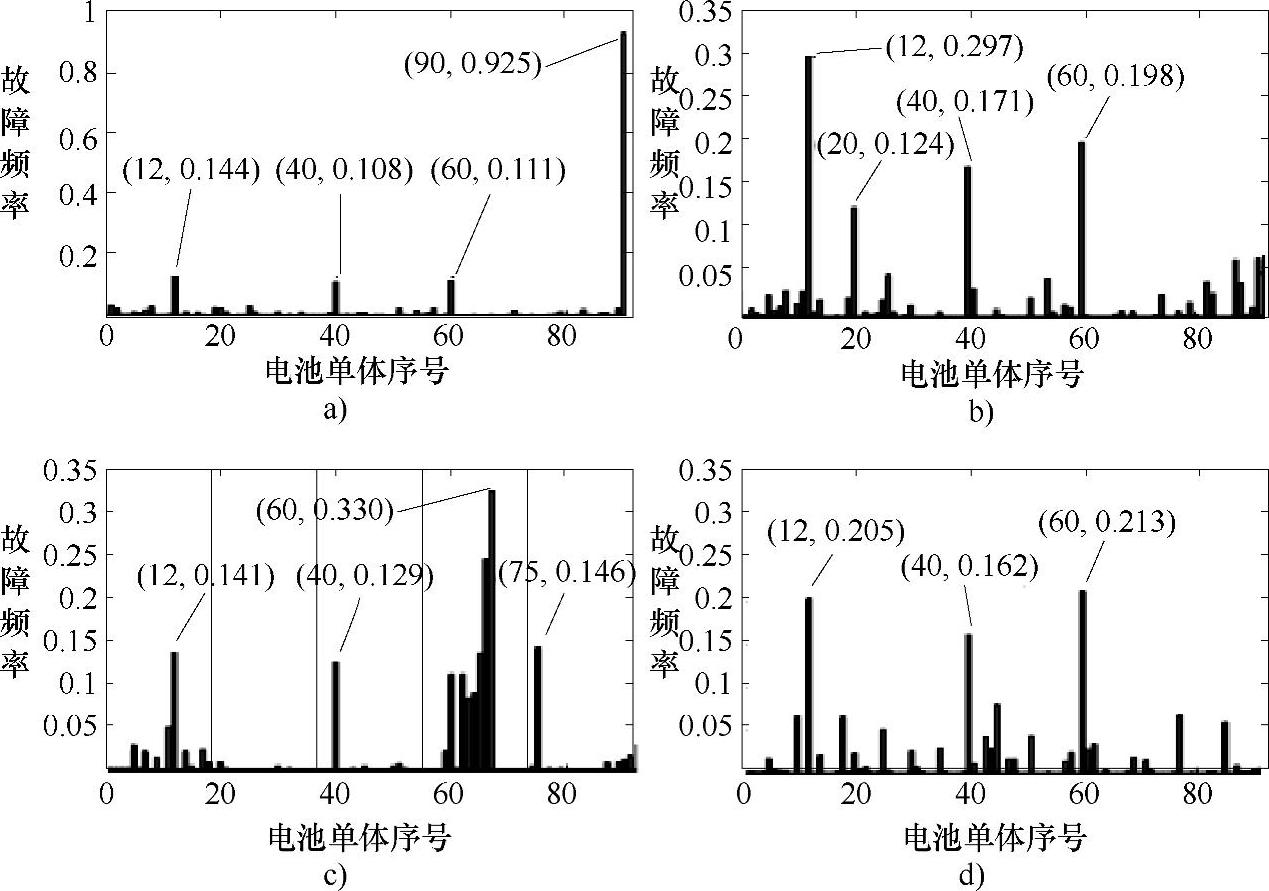
图5-9 两种类型的故障对比

（2）实车对照分析

建立3层的BP神经网络来对第二种故障进行特征拟合。用大量的数据样本对诊断结果进行计算，第二种故障的统计规律如图5-10所示。其中位置编号为12、40、60的电池单体，故障程度较为严重。下面对此数据挖掘规律并进行实车对应分析。

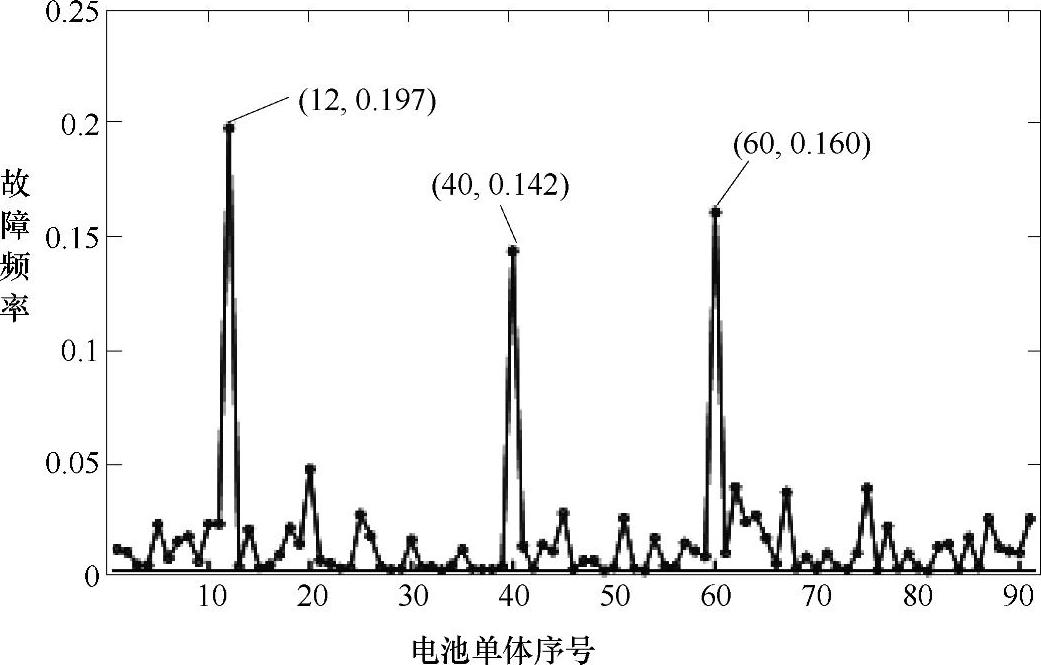
图5-10 神经网络拟合第二种故障的统计规律

研究的某车型的电池组排布如图5-11所示。从图中可以看出电池组的排布为：1～58号电池为卧式排布；59～91为立式排布。我们用三维视图对电池组中单体进行描述，并将故障电池单体及其临近部分在实车电池组中用红色圆圈标识出来，如图5-12所示。实车对照的诊断结果表明在纯电动汽车的电池组的前底部，电池单体的故障概率更大。

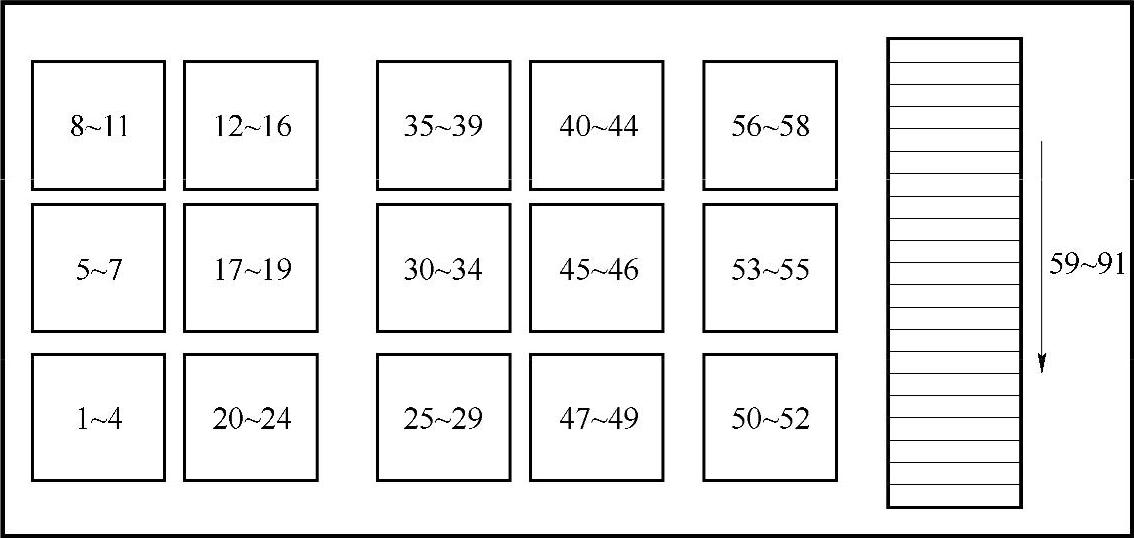
图5-11 电池组排布图

4.在时间维度上电池的故障诊断

（1）建立以天为单位的时间维度上的月度诊断模型

为了分析在一段时间内的电池故障状态的特性和变化，本案例建立了以天为单位的纯电动汽车电池故障月度分析。将车辆的电池故障状态以天为单位进行统计和分析，得到在短期时间跨度的情况下，电池故障状态的改变。其算法如下：

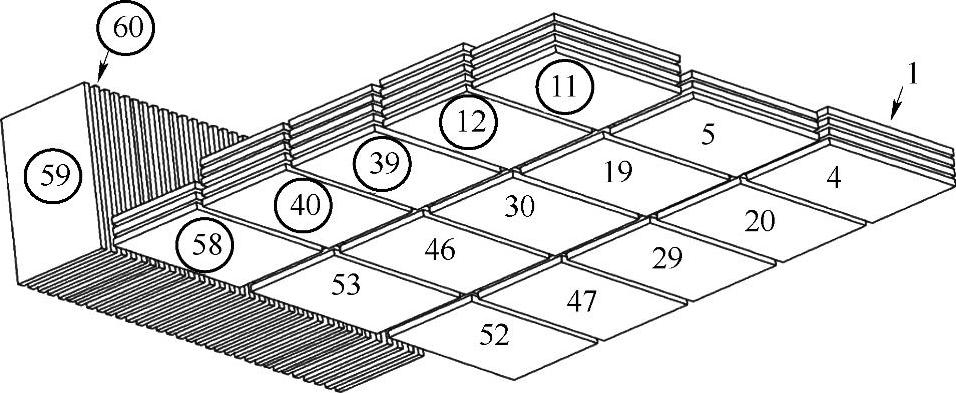
图5-12 实车故障发生位置

纯电动汽车单体端电压数据：

U_mouth=（U₁^T，U₂^T，…，U_i^T）^T （5-19）

式中，U_mouth是一个月内车辆电池单体端电压所构成的数据矩阵；U_i是车辆每天电池单体端电压构成的数据矩阵。经故障诊断算法计算后，得到整月的故障矩阵为

R_mouth=（R₁^T，R₂^T，…，R_i^T）^T （5-20）

式中，R_mouth是整月的故障矩阵；R_i是第i天的故障矩阵。

一个月的故障频率矩阵由故障矩阵计算得

式中，i是第i天的故障矩阵；j指电池单体在电池组中的编号；FFⁱ_mouth是电池组中第j个电池单体整月的故障频率；R^i，j_outh是R_mouth矩阵中第i行j列的值。

FF_mouth=（FF¹_mouth，…，FFⁱ_mouth，…，FFⁿ_mouth） （5-22）

式中，FF_mouth是整个月份的故障频率矩阵。

整月的故障频率矩阵如图5-13所示，从图中可以得到在以月份为跨度的时间段内，电池单体的性能状态是基本稳定的，故障位置和故障程度也相对稳定，不会发生较大的改变。

（2）建立以季度为单位的时间维度上的年度诊断模型

为了分析在较大时间跨度上的纯电动汽车电池的故障特性和变化，建立以季度为单位的年度故障诊断分析模型。下面分析北京地区纯电动汽车全年的故障情况，以季度为单位运用神经网络模型拟合每个季度的故障分布。

纯电动汽车单体端电压数据为

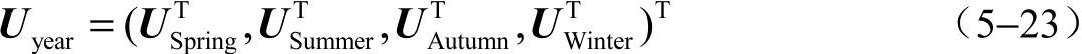
式中，U_year是全年的电动车辆电池单体端电压矩阵；U_Spring、U_Summer、U_Autumn和U_Winter分别是四个季度的纯电动汽车电池单体端电压矩阵。

春、夏、秋、冬四季电池电压数据为

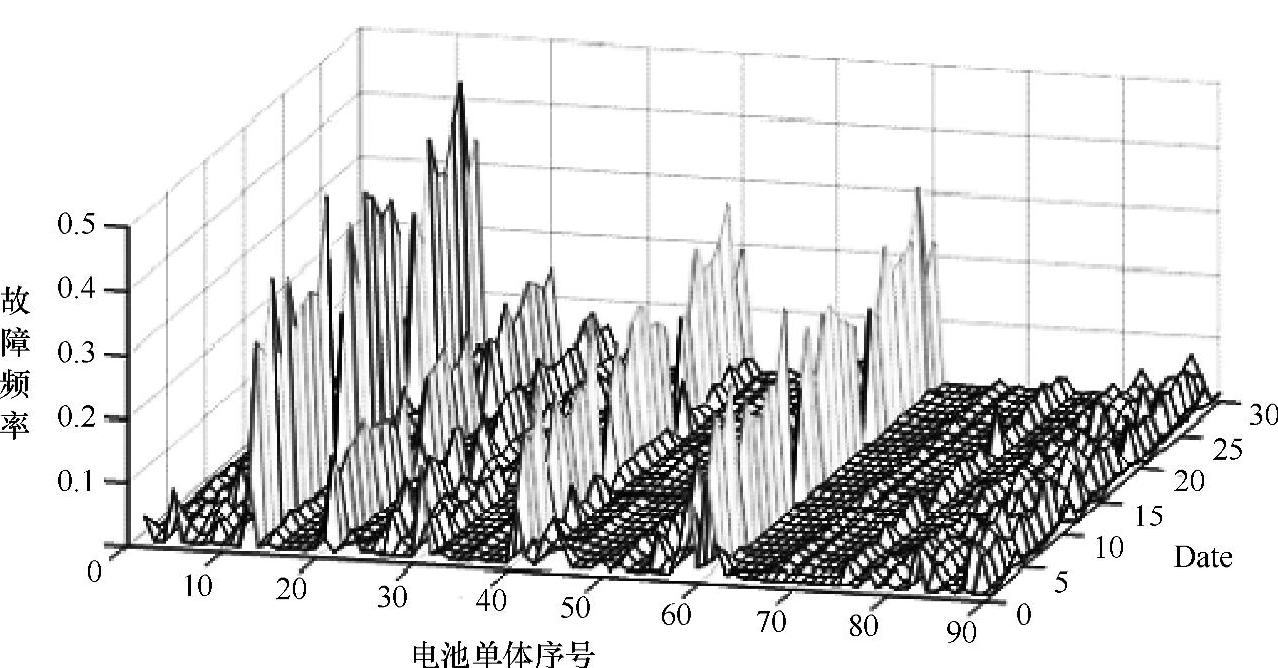
图5-13 整月故障频率矩阵

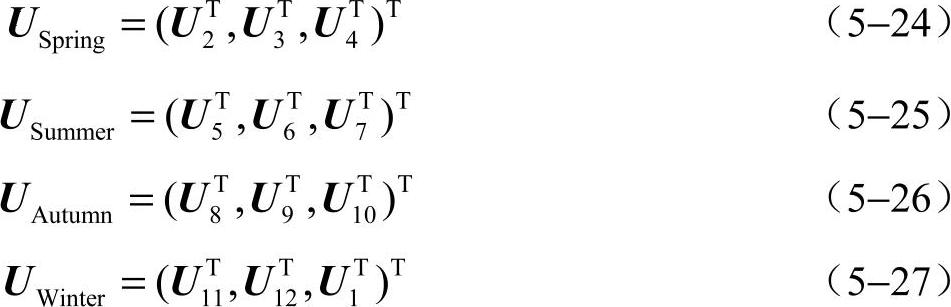
式中，U₁～U₁₂分别为1月～12月的电池单体端电压数据矩阵。

四季的故障频率为

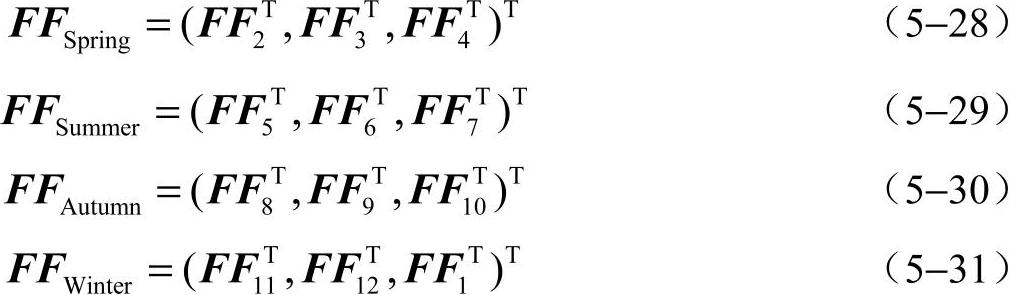
式中，FF₁～FF₁₂分别为1月～12月的故障矩阵。

如图5-14所示，在北京地区，当车辆运行在春、夏、秋三个季节时，电池运行的性能差距较小，故障的位置和频率相对稳定。然而在冬季，电池故障频率上升得非常显著。四个季节的电池故障频率为[0.0200，0.0191，0.0195，0.0384]。其值在夏季最低，在冬季最高，并且在冬季故障频率比其他三个季节平均要高出96%。同时，这个结果也量化地反映了电池在冬季的故障程度。

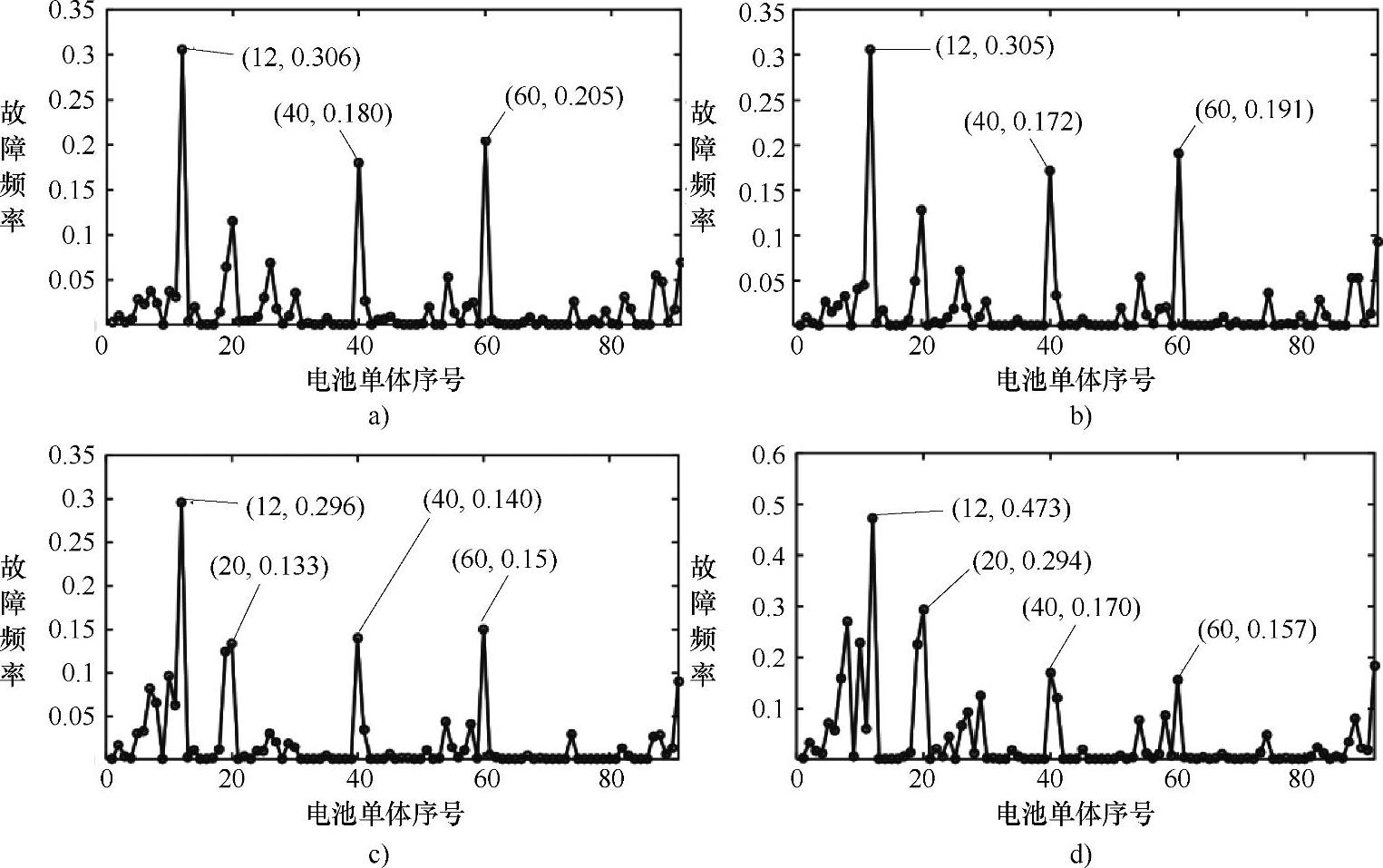
图5-14 四个季节电池故障频率