季节变动分析是分析一个季节周期内时间序列在各个时期的强弱变化规律。需要注意的是,如果时间序列给出的是年度数据,则每项数据都包含了完整的季节周期,序列不再包含季节变动因素,不需要进行季节变动分析。
如果对时间序列采用乘法模型分析,则其中的季节变动规律用季节指数来表示。季节指数是一个相对数,季节指数大于1表示该季为旺季,小于1表示淡季,接近1则表示平季。各个季节指数相加应等于一个周期中的季节指数个数。如果对时间序列采用加法模型分析,则其中的季节变动用季节差表示,季节差属于绝对数,季节差大于0表示该季为旺季,小于0表示淡季,接近0则表示平季。各个季节差相加应等于0。
实际分析季节变动时,以季节指数使用较多。如果各期的季节指数比较接近,则说明季节变动不明显或不存在季节变动;否则,即为存在季节变动。
分析季节变动一般需要三个以上季节周期的数据。按照是否消除长期趋势的影响,季节变动分析方法分为同期简单平均法和趋势剔除法两种。
1.同期简单平均法
同期简单平均法是对各个同期水平分别计算平均数,然后与全部数据的总平均数相比,计算季节指数。比如,根据各年度的月度数据分析季节变动,则有1~12月12个季节指数;根据各年度的季度数据分析季节变动,则有1~4季4个季节指数;根据若干周每天的数据分析季节变动,则有星期一至星期天7个季节指数;等等。
同期简单平均法消除了不规则变动的影响,是分析季节变动最基本的方法。
2.趋势剔除法
简单同期平均没有考虑长期趋势对季节变动的影响,只适用于长期趋势不明显的序列。但社会经济现象一般都有明显的上升或下降的长期趋势。如果序列有明显上升的长期趋势,则会影响四个季度的季节指数依次上升;如果序列有明显下降的长期趋势,则会影响四个季度的季节指数依次下降。因此,只有消除长期趋势,才能得到准确的季节变动规律。(https://www.xing528.com)
剔除长期趋势的具体步骤是:
①首先对原序列(Y)按季节周期进行移动平均,得到的移动平均序列(M)消除了季节因素和不规则因素的影响,只包含长期趋势和循环变动因素。
②然后用原序列(Y)除以移动平均序列(M)得到一个新序列(F),此序列只包含季节变动和不规则变动。
③最后对包含季节变动和不规则变动的序列(F)采用简单同期平均法可计算出季节指数。
上述过程可用图4-19表示。
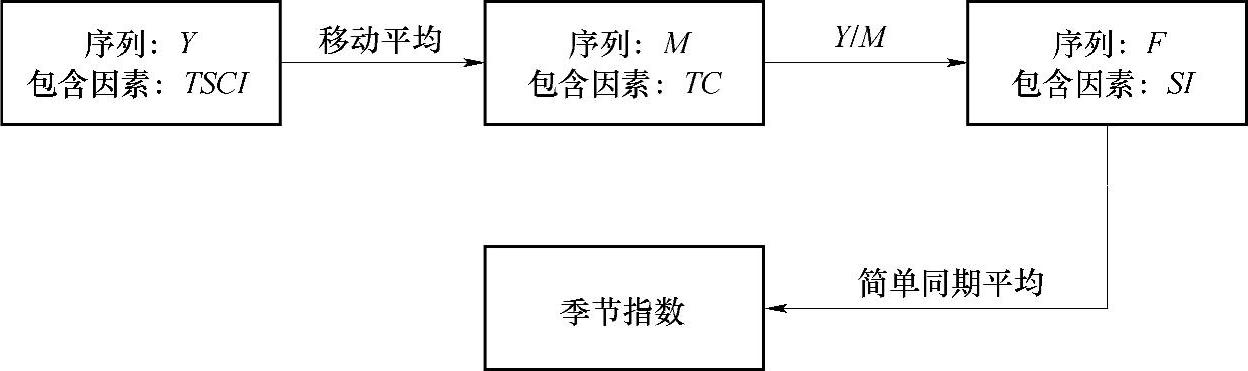
图4-19 趋势剔除法测定季节指数流程图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




