新能源汽车趋势分析：长期趋势

长期趋势分析是时间序列分析中最基本的内容。分析长期趋势的目的可以概括为以下几个方面：首先是认识长期趋势本身的定量规律性；其次是认识时间序列变化中非趋势的其他成分的变化规律，这里的非趋势成分是指时间序列数据中提出趋势成分后剩下的数据序列；最后是可以基于趋势成分变化的规律性来预测时间序列未来的变化。

时间序列趋势分析的方法比较多，常用的有移动平均法、指数平滑法和趋势模型法等。

1.移动平均法

移动平均法是一种应用广泛的简单趋势分析技术，它是从序列的第一项开始，按一定的项数计算序时平均，依次向后移动得到一个新的移动平均序列。由于移动平均序列消除了偶然因素的干扰，因而依据新的序列比较容易观察现象发展变化的长期趋势。假设按k项移动平均，则移动平均序列为

应用移动平均法时，确定移动的项数很关键，通常遵循如下原则：一是项数要适中，项数太多虽然较容易观察出长期趋势，但也意味着损失更多的信息，项数太少则不容易消除偶然因素的干扰；二是当数据是以时间周期形式给出时，应取周期项数或其整数倍移动，如序列为若干年的月度数据，则应取12项移动平均；三是尽可能取奇数项移动，因为移动平均的结果应该与原序列的中间项对应，当选择偶数项移动平均时，需要对移动平均的结果再次进行两项移动平均才能与原序列对齐。

移动平均法能够很好地消除季节因素和不规则因素的影响，不仅可用于分析时间序列的长期趋势，还经常用于对序列进行修正。因为移动平均序列项数变少，移动平均法损失的信息较多，所以该方法不适合直接用于外推预测。

2.指数平滑法

在移动平均法中，假定过去k期观测值的权重相等，并且没有考虑早期的信息。但在很多情况下，最近的观测值比早期观测值包含更多对于认识现象未来变化有用的信息，而指数平滑法则较好地体现了这一原则。

指数平滑法是以平滑系数为权数，利用本期观测值和本期预测值共同构造下一期预测值的一种加权平均方法。指数平滑法有一次指数平滑、二次指数平滑、H次指数平滑等，此处仅介绍一次指数平滑，其公式如下：

T_t+1=αy_t+（1-α）T_t （t=1，2，…，n） （4-101）式中，y_t为t期的实际观测值；T_t和T_t+1分别为t期和t+1期的平滑预测值；α为平滑系数（0＜α＜1），其取值越大代表当前已观测到的信息在预测中的作用越大。在实际应用中，通常可选取几个α进行预测，最终选取预测误差最小的α作为最后的平滑系数。

对上述一次指数平滑公式展开，则有：

由上面的展开式可以看出，早期观测值的系数按照指数规律递减，越早期的观测值系数越小。当序列项数较多时，初始值对平滑预测值的影响可以忽略，因此，初始平滑值可以取初始观测值T₁=y₁。(www.xing528.com)

指数平滑方法能够较好地消除不规则因素的影响，特别适合于具有特殊惯性趋势形态的序列，不适合具有某种曲线趋势的序列。此外，该方法只适合直接外推预测近期的趋势值，不能预测远期的趋势值。

3.趋势模型法

当时间序列的长期趋势呈近似直线或某种曲线变化规律时，适合采用模型法对其长期趋势进行分析预测。采用模型法进行趋势预测的优点是可以对未来较远时期的趋势值进行预测，而且还可对模型进行各种统计检验。

模型法是以时间t为自变量，以实际观测值y为因变量建立回归模型，利用回归分析方法估计模型参数，并在此基础上对序列的趋势进行预测的方法。根据长期趋势的形态，模型法分为直线模型和曲线模型两类。

选用何种模型分析时间序列的长期趋势，主要基于以下四点：一是要对现象发展变化的驱动力量进行定性分析，不能只注重数据和形式上的趋势变化；二是将观测值绘成折线图，从图形判断其趋势符合哪种形式；三是分别配合多种模型，选取误差最小的模型；四是对于变化复杂的时间序列，可以考虑分段配合不同的模型。

（1）直线回归模型测定长期趋势

当时间序列的长期趋势近似呈直线形式时，可配合线性回归模型对时间序列的长期趋势进行分析，配合的一般线性方程为

式中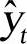，为趋势值或预测值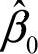；和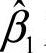为模型参数，可采用回归分析中的最小二乘方法对参数进行估计。其推导过程见回归分析相关内容，结果为

（2）曲线回归模型测定长期趋势

对于长期趋势呈曲线形式的时间序列，应该配合曲线模型对趋势变化进行分析。时间序列中常见的曲线趋势模型有抛物线、指数曲线、对数曲线、Logistic曲线等。曲线模型的参数估计可参见本书回归分析中非线性回归的相关内容，此处仅介绍二次抛物线模型分析长期趋势。测定长期趋势的二次抛物线回归方程形式如下：