离群点诊断：统计方法运用

1.理论基础

最早的离群点挖掘算法大多是基于统计学原理或分布模型实现的，通常可以分为基于分布的方法和基于深度的方法两类。一般地，讨论基于统计的离群点挖掘主要指的是基于分布的方法。

基于统计的离群点诊断的基本思想是基于这样的事实：符合正态分布的对象（值）出现在分布尾部的机会很小。例如，对象落在距均值3个标准差的区域以外的概率仅有0.0027。更一般地，当x为属性值时，|x|≥c的概率随c的增加而迅速减小。设α=p（|x|≥c），表4-3显示当分布为N（0，1）时，c的某些样本值和对应的α值。从表4-3可以看出，离群值超过4个标准差的值出现的可能性是万分之一。

表4-3 落在标准差的中心区域以外的概率

为了更清晰地表现基于统计的离群点诊断原理，可以绘制图4-18所示的离群点分布带示意图。该图在实践中具有重要的意义，对于观测样本x，我们可以这样理解该图：

①如果此点在上、下警告线之间区域内，则数据处于正常状态。

②如果此点超出上、下警告线，但仍在上、下控制线之间的区域内，则提示质量开始变劣，可能存在“离群”倾向。

③若此点落在上、下控制线之外，则表示数据已经“离群”，这些点即被诊断出的离群点。

如果（正常对象的）一个感兴趣的属性的分布是具有均值μ和标准差σ的正态分布，则可以通过变换z=（x-μ）/σ转换为标准正态分布N（0，1）。通常μ和σ是未知的，可以通过样本均值和样本标准差来估

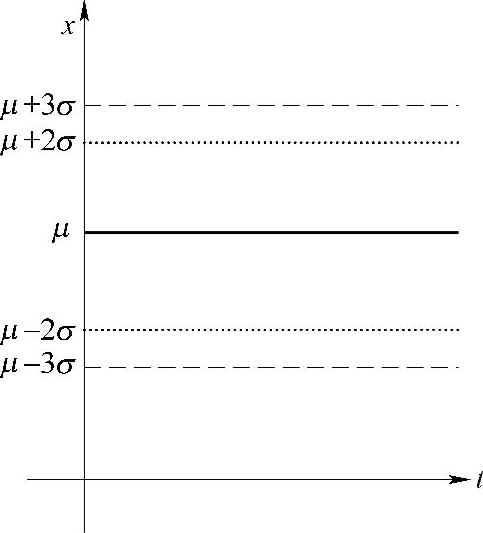
图4-18 离群点分布带示意图

计。实践中，当观测值很多时，这种估计的效果很好；另外，由概率统计中的大数定律可知，在大样本的情况下可以用正态分布近似其他分布。

基于统计的方法需要使用标准统计分布（如标准正态分布）来拟合数据点，然后根据概率分布模型采用不一致性检验来确立离群点。因此基于统计的离群点诊断方法要求事先知道数据集的统计分布、分布参数（如均值和方差）、预期的离群点数目和离群点类型等。

基于分布的方法的优缺点都很明显。其优点主要是易于理解，实现起来也比较方便，并且对数据分布满足某种概率分布的数值型单维数据集较为有效。但在多数情况下数据分布是未知的，也就很难建立某种确定的概率分布模型。同时，在实际中往往要求在多维空间中发现离群点，而绝大多数统计检验是针对单个属性的。因此，当没有特定的检验时，基于分布的方法不能确保发现所有的异常，或者观测到的分布不能恰当地被任何标准的分布来拟合^[1]。

Grabbs导出了统计量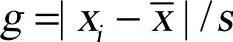的分布。取显著水平α，可以得到临界值g₀，使得：(www.xing528.com)

其中，。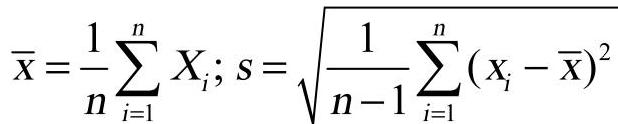

若某一个测量数据x_i满足下式时，则认为数据为异常数据而把它剔除：

式中，g₀可以通过查询专门的g₀表得到。

如果一次可以判断两个或两个以上的数据是异常数据，则只将其中使得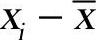最大的数据剔除。然后，重新计算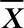、g₀、s，再一次迭代寻找异常数据。如此循环进行，直到找不出离群点为止。

具体算法如下：

①求出样本均值x和样本标准差s。根据给定的显著水平α和样本容量n，查表求出g₀。

②计算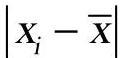，i=1，2，…n，找出x_k使得：

③若有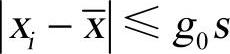，则认为数据中无异常数据；否则认为x_k是异常数据，将之从数据中剔除。

重复步骤①～③，直到数据中无异常数据为止。

在实践中，对于临界值g₀，从严格的角度，可以通过查表给出具体的值。但通常的做法就是直接给出，比如取1、2或3，甚至小数。具体取多大的值，取决于数据的量及对离群点诊断的严格程度。

2.优点与缺点

离群点诊断的统计学方法具有坚实的基础，建立在标准的统计学技术（如分布参数的估计）之上。当存在充分的数据和所用的检验类型时，诊断离群点非常有效。对于单个属性，存在各种统计离群点诊断方法。对于多元数据，很难同时对多维数据使用基于统计的离群点诊断方法，通常还需要按照单个变量的方法进行诊断。