贝叶斯分类器：原理、性能与相关属性

1.贝叶斯分类原理

贝叶斯分类是一类分类算法的总称，这类算法均以贝叶斯定理为基础，故统称为贝叶斯分类。

贝叶斯分类是一类利用概率统计知识进行分类的算法，其分类原理是贝叶斯定理。贝叶斯定理是由18世纪概率论和决策论的早期研究者Thomas Bayes提出的，故用其名字命名。

贝叶斯定理（Bayes＇theorem）是概率论中的一个结果，它与随机变量的条件概率以及边缘概率分布有关。在有些关于概率的解说中，贝叶斯定理能够告知我们如何利用新证据修改已有的看法。通常，事件A在事件B（发生）的条件下的概率，与事件B在事件A的条件下的概率是不一样的；然而，这两者是有确定的关系，贝叶斯定理就是这种关系的陈述。

假设X、Y是一对随机变量，它们的联合概率P（X=x，Y=y）是指X取值x且Y取值y的概率。条件概率是指一个随机变量在另一个随机变量取值已知的情况下取某一特定值的概率。例如，条件概率P（Y=y|X=x）是指在变量X取值x的情况下，变量Y取值y的概率。X和Y的联合概率和条件概率满足如下关系：

P（Y，X）=P（Y|X）P（X）=P（X|Y）P（Y） （4-70）

对式（4-70）变形，可得到下面的公式，称为贝叶斯定理：

贝叶斯定理很有用，因为它允许我们用先验概率P（Y）、条件概率P（X|Y）和证据P（X）来表示后验概率。而在贝叶斯分类器中，朴素贝叶斯最为常用，接下来将介绍朴素贝叶斯的原理。

2.朴素贝叶斯分类原理

朴素贝叶斯分类是一种十分简单的分类算法，之所以如此命名，是因为这种方法的思想真的很朴素。朴素贝叶斯的思想基础是这样的：对于给出的待分类项，求解在此项出现的条件下各个类别出现的概率，哪个最大，就认为此待分类项属于哪个类别。通俗来说，例如，在医生给患者看病时，患者所描述的症状为打喷嚏，在患者还没有做任何检查之前，医生仅能根据通常情况判断患者为感冒引起的打喷嚏，因为由感冒引起的打喷嚏概率比较大。在我们没有其他信息可以参考的时候，我们选择信任较大概率的事件，这就是朴素贝叶斯的基本思想。

朴素贝叶斯分类器以简单的结构和良好的性能受到人们的关注，是最优秀的分类器之一。朴素贝叶斯分类器建立在一个类条件独立性假设（朴素假设）基础之上：给定类节点（变量）后，各属性节点（变量）之间相互独立。根据朴素贝叶斯的类条件独立假设，有：

条件概率P（X₁|C_i），P（X₂|C_i），…，P（X_n|C_i），可以从训练数据集求得。根据此方法，对一个未知类别的样本X，可以先分别计算出X属于每一个类别C_i的概率P（X|C_i）P（C_i），然后选择其中概率最大的类别作为其类别。

朴素贝叶斯分类的步骤如下：

步骤1：设x={a₁，a₂，…，a_m}为一个待分类项，而每个a为x的一个特征属性。

步骤2：有类别集合C={y₁，y₂，…，y_n}。

步骤3：计算P（y₁|x），P（y₁|x），…，P（y₁|x）。

步骤4：如果P（y_k|x）=max{P（y₁|x），P（y₂|x），…，P（y_n|x）}，则x∈y_k。

那么现在的关键就是如何计算步骤3中各个条件的概率，我们可以这么做：

①找到一个已知分类的待分类项集合，这个集合叫作训练样本集。(www.xing528.com)

②统计得到在各类别下各个特征属性的条件概率估计，即

P（a₁|y₁），P（a₂|y₁），…，P（a_m|y₁）；P（a₁|y₂），P（a₂|y₂），…，P（a_m|y₂）；…；P（a₁|y_n），P（a₂|y_n），…，P（a_m|y_n）

③如果各个特征属性是条件独立的，则根据贝叶斯定理有如下推导：

因为分母对于所有类别为常数，因此只要将分子最大化即可，因为各特征属性是条件独立的，所以有

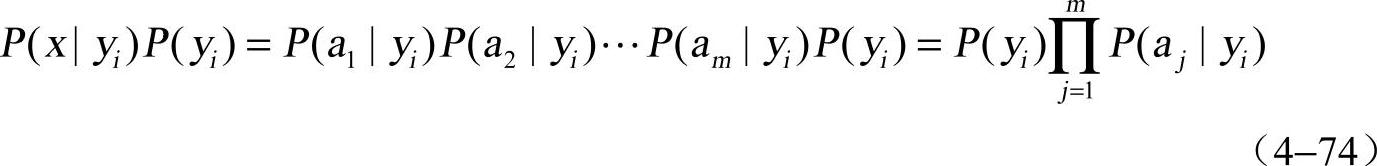
根据上述分析，朴素贝叶斯分类的流程可以由图4-15表示（暂时不考虑验证）。

可以看到，整个朴素贝叶斯分类分为三个阶段：

第一阶段：准备工作阶段。这个阶段的任务是为朴素贝叶斯分类做必要的准备，主要工作是根据具体情况确定特征属性，并对每个特征属性进行适当划分，然后由人对一部分待分类项进行分类，形成训练样本。这一阶段的输入是所有待分类数据，输出是特征属性和训练样本。这一阶段是整个朴素贝叶斯分类中唯一需要人工完成的阶段，其质量将对整个过程有重要影响，分类器的质量在很大程度上由特征属性、特征属性划分及训练样本决定。

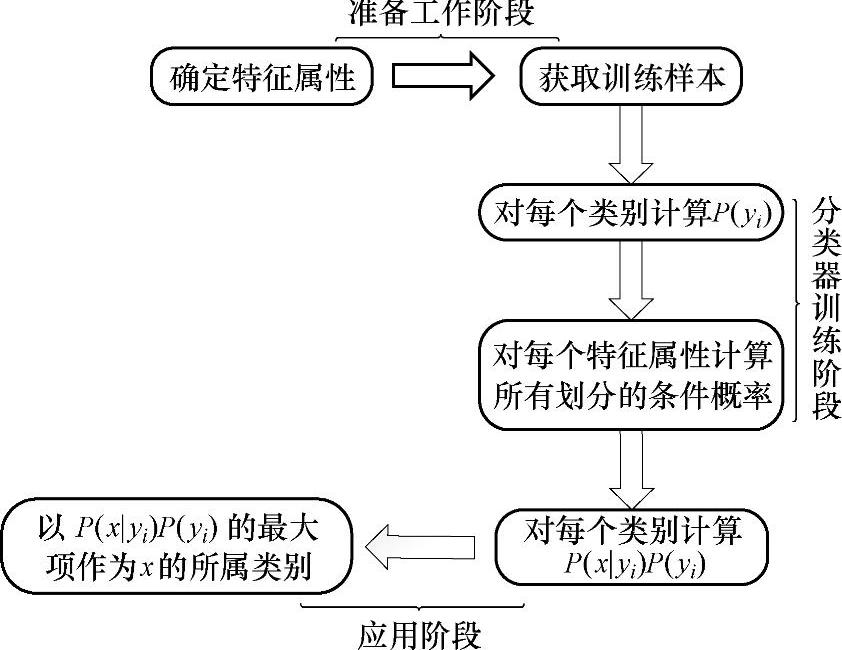
图4-15 朴素贝叶斯算法分类流程图

第二阶段：分类器训练阶段。这个阶段的任务就是生成分类器，主要工作是计算每个类别在训练样本中的出现频率及每个特征属性划分对每个类别的条件概率估计，并记录结果。其输入是特征属性和训练样本，输出是分类器。这一阶段是机械性阶段，根据前面讨论的公式可以由程序自动计算完成。

第三阶段：应用阶段。这个阶段的任务是使用分类器对待分类项进行分类，其输入是分类器和待分类项，输出是待分类项与类别的映射关系。这一阶段也是机械性阶段，由程序完成。

朴素贝叶斯算法成立的前提是各属性之间相互独立。当数据集满足这种独立性假设时，分类的准确度较高，否则可能较低。另外，该算法没有分类规则输出。

在许多场合，朴素贝叶斯（Naive Bayes，NB）分类可以与决策树和神经网络分类算法相媲美，该算法能运用到大型数据库中，且方法简单、分类准确率高、速度快。因为贝叶斯定理假设一个属性值对给定类的影响独立于其他的属性值，而此假设在实际情况中经常是不成立的，所以其分类准确率可能会下降。为此，出现了许多降低独立性假设的贝叶斯分类算法，如TAN（Tree Augmented Bayes’Network）算法、贝叶斯网络分类器（Bayesian Network Classifier，BNC）。

3.朴素贝叶斯特点

朴素贝叶斯分类器一般具有以下特点。

①简单、高效、健壮。面对孤立的噪声点，朴素贝叶斯分类器是健壮的，因为在从数据中估计条件概率时，这些点被平均，另外朴素贝叶斯分类器也可以处理属性值遗漏问题。而面对无关属性，该分类器依然是健壮的。因为如果X_i是无关属性，那么P（X_i|Y）几乎变成了均匀分布，X_i的类条件概率不会对总的后验概率的计算产生影响。

②相关属性可能会降低朴素贝叶斯分类器的性能，因为对这些属性，条件独立的假设已不成立。