新能源汽车大数据分析和应用技术：近邻方法和示意图

1.K-近邻原理

K-近邻（K-Nearest Neighbor，KNN）算法是一种基于实例的分类方法，最初由Cover和Hart于1968年提出，是一种非参数的分类技术。

K-近邻分类方法通过计算每个训练样例到待分类样品的距离，取和待分类样品距离最近的K个训练样例。K个样品中哪个类别的训练样例占多数，则待分类元组就属于哪个类别。使用最近邻确定类别的合理性可用下面的谚语来说明：“如果走像鸭子，叫像鸭子，看起来还像鸭子，那么它很可能就是一只鸭子”，如图4-12所示。最近邻分类器把每个样例看作d维空间上的一个数据点，其中d是属性个数。给定一个测试样例，我们可以计算该测试样例与训练集中其他数据点的距离（邻近度），给定样例z的K-最近邻是指找出和z距离最近的K个数据点。

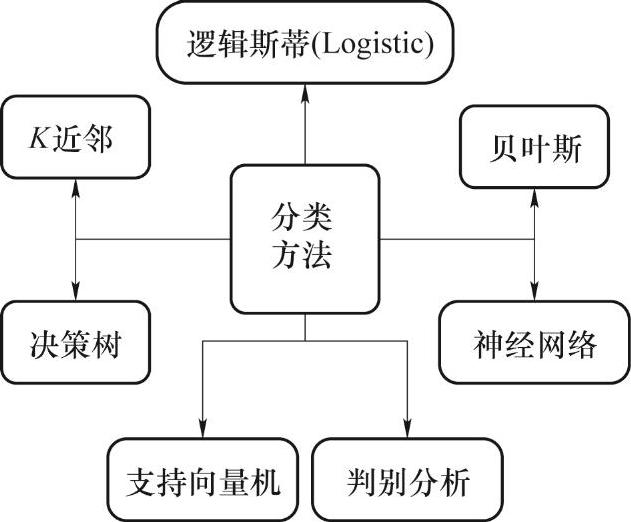
图4-11 常用的分类方法

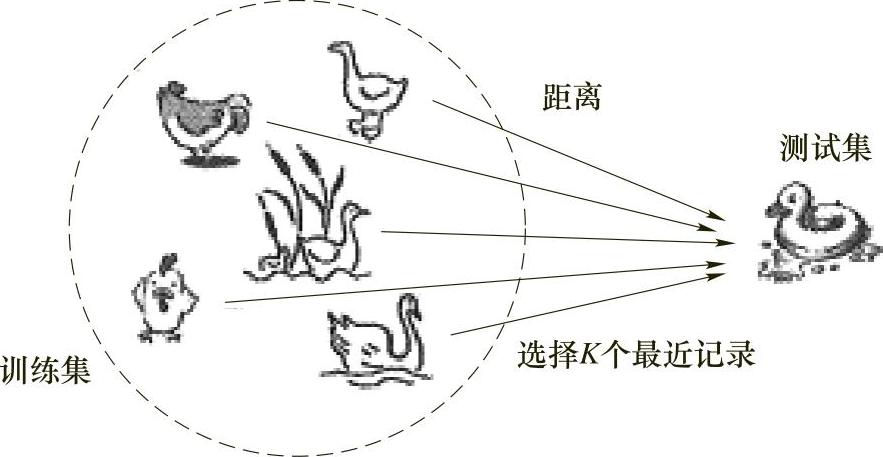
图4-12 KNN方法原理示意图

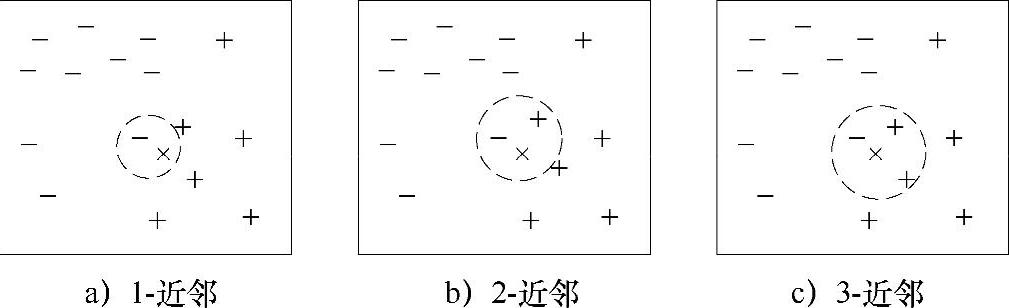
图4-13给出了位于圆圈中心的数据点的1-最近邻、2-最近邻和3-最近邻。该数据点根据其近邻的类标号进行分类。如果数据点的近邻中含有多个类标号，则将该数据点指派到其最近邻的多数类。在图4-13a中，数据点的1-最近邻是一个负例，因此该点被指派到负类。如果最近邻是三个，如图4-13c所示，其中包括两个正例和一个负例。根据多数表决方案，该点被指派到正类。在最近邻中正例和负例个数相同的情况下（图4-13b），可随机选择一个类标号来分类该点。

KNN算法具体步骤如下：

步骤1：初始化距离为最大值。

步骤2：计算未知样本和每个训练样本的距离dist。

步骤3：得到目前K个最近邻样本中的最大距离maxdist。

步骤4：如果dist小于maxdist，则该训练样本作为K-最近邻样本。

(www.xing528.com)

图4-13 实例

步骤5：重复步骤2～步骤4，直到未知样本和所有训练样本的距离都算完。

步骤6：统计K个最近邻样本中每个类别出现的次数。

步骤7：选择出现频率最高的类别作为未知样本的类别。

根据KNN算法的原理和步骤可以看出，KNN算法对K值的依赖较高，所以K值的选择非常重要。如果K太小，则预测目标容易产生变动性；如果K太大，最近邻分类器可能会误分类测试样例，因为最近邻列表中可能包含远离其近邻的数据点（图4-14）。推定K值的有益途径是通过有效参数的数目这个概念，有效参数的数目是和K值相关的，大致等于n/K。其中，n是这个训练数据集中实例的数目。在实践中往往通过若干次实验来确定K值，取分类误差率最小的K值。

2.K-近邻特点

用KNN方法在类别决策时，只与极少量的相邻样本有关，因此，采用这种方法可以较好地避免样本的不平衡问题。另外，由于KNN方法主要是靠周围有限的邻近的样本，而不是靠判别类域的方法来确定所属类别，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。

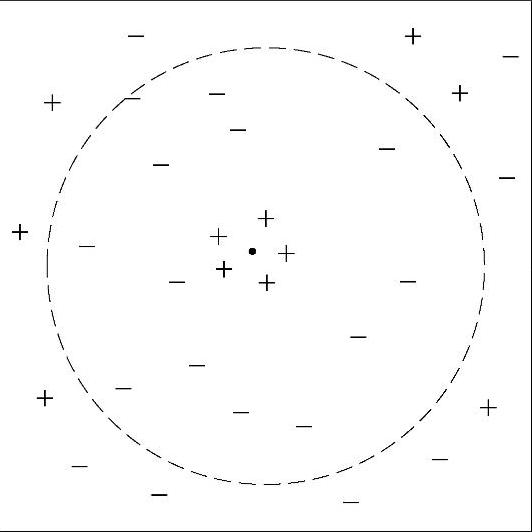
图4-14 K较大时的K-最近邻分类

该方法的不足之处是计算量较大，因为对每一个待分类的样本都要计算它到全体已知样本的距离，才能求得它的K个最近邻点。针对该不足，主要有以下两类改进方法：

①对于计算量大的问题目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。这样可以挑选出对分类计算有效的样本，使样本总数合理地减少，以同时达到减少计算量又减少存储量的双重效果。该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

②对样本进行组织与整理，分群分层，尽可能地将计算压缩在接近测试样本领域的小范围内，避免盲目地与训练样本集中的每个样本进行距离计算。

总体来说，该算法的适应性强，尤其适用于样本容量比较大的自动分类问题，而对于那些样本容量较小的分类问题，采用这种算法比较容易产生误分。