新能源汽车大数据分析：聚类方法概要

1.聚类的概念

将物理或抽象对象的集合分成由类似的对象组成的多个类或簇（Cluster）的过程被称为聚类（Clustering）。由聚类所生成的簇是一组数据对象的集合，这些对象与同一个簇中的对象相似度较高，与其他簇中的对象相似度较低。相似度是根据描述对象的属性值来度量的，距离是经常采用的度量方式。分析事物聚类的过程称为聚类分析或者群分析，它是研究（样品或指标）分类问题的一种统计分析方法。

在许多应用中，簇的概念都没有严格的定义。为了理解确定簇构造的困难性，可参考图4-4。该图显示了18个点和将它们划分成簇的3种不同方法。标记的形状指示簇的隶属关系。图4-4b和图4-4d分别将数据划分成两部分和六部分。然而，将2个较大的簇都划分成3个子簇可能是人的视觉系统造成的假象。此外，说这些点形成4个簇（图4-4c）可能也不无道理。该图表明簇的定义是不精确的，而最好的定义依赖于数据的特性和期望的结果。另外，簇的形象表现在空间分布上也不是确定的，而是成各种不同的形状，在二维平面里就可以有各种不同的形状，如图4-5所示，在多维空间里，有更多的形状。因此簇的定义，也需要具体情况具体分析，但总的趋势是，同一个簇的样本在空间上是靠拢在一起的。

图4-4 相同点集的不同聚类方法

a）原来的点 b）2个簇 c）4个簇 d）6个簇

聚类分析与其他将数据对象分组的技术相关。例如，聚类可以看作一种分类，它用类（簇）标号创建对象的标记。然而，只能从数据导出这些标号。相比之下，分类是监督分类（Supervised Classification），即使用由类标号已知的对象开发的模型，对新的、无标记的对象赋予类标号。为此，有时称聚类分析为非监督分类（Unsupervised Classification）。

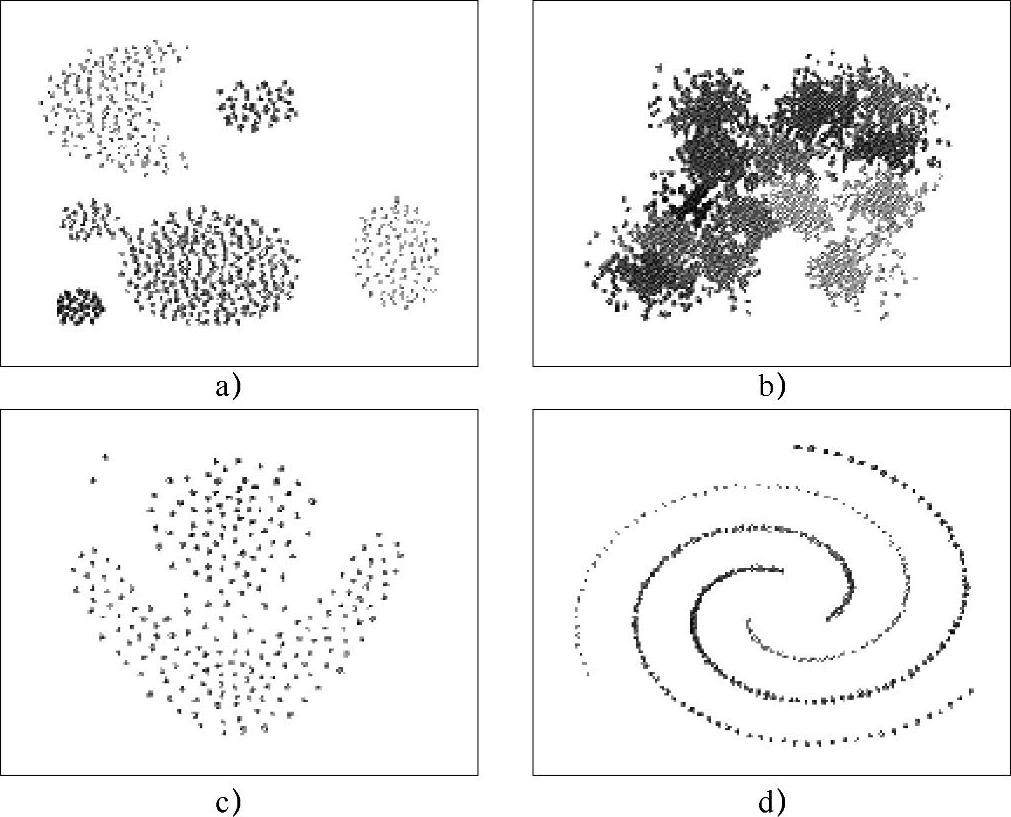
图4-5 常见的类别特征

此外，尽管分割（Segmentation）和划分（Partitioning）这两个术语有时也用作聚类的同义词，但是这些术语通常用来表示传统的聚类分析之外的方法。例如，划分（Partitioning）通常用在与将图分成子图相关的技术，与聚类并无太大联系。分割（Segmentation）通常指使用简单的技术将数据分组；例如，图像可以根据像素亮度或颜色分割，人可以根据他们的收入分组。尽管如此，图划分、图像分割和市场分割的许多工作都与聚类分析有关。

2.类的度量方法

既然要研究聚类，我们就有必要了解不同类的度量方法。纵然类的形式各有不同，但总的来说，常用的类的度量方法有两种，即距离和相似系数。距离用来度量样品之间的相似性，相似系数用来度量变量之间的相似性。

（1）距离

设X₁，X₂，…，Xn为取自p元总体的样本，记第i个样品为X_i=（x_i1，x_i2，…，x_ip）（i=1，2，…，n）。聚类分析中常用的距离有以下几种：

①明可夫斯基（Minkowski）距离。第i个样品X_i和第j个样品X_j之间的明可夫斯基距离（也称“明氏距离”）定义为

其中，q为正整数。

特别地，

当q=1时，为绝对值距离。

当q=2时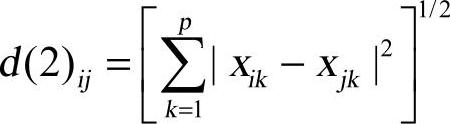，为欧式距离。

当q→∞时，为切比雪夫距离。

注意：当各变量的单位不同或测量值范围相差很大时，不应直接采用明可夫斯基距离，应先对各变量的观测数据做标准化处理。(www.xing528.com)

②兰氏（Lance和Williams）距离。当x_ik＞0（i=1，2，…，n；j=1，2，…p）时，定义第i个样品X_i和第j个样品X_j之间的兰氏距离为

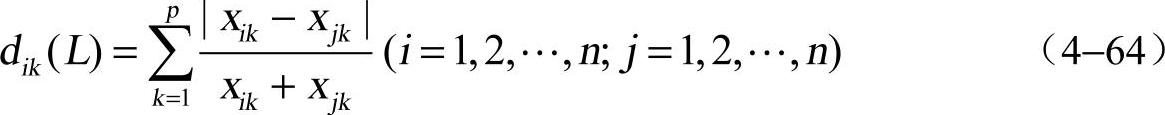
兰氏距离与各变量的单位无关，它对大的异常值不敏感，故适用于高度斜偏的数据。

③马哈拉诺比斯（Mahalanobis）距离。第i个样品X_i和第j个样品X_j之间的马哈拉诺比斯距离（简称“马氏距离”）定义为

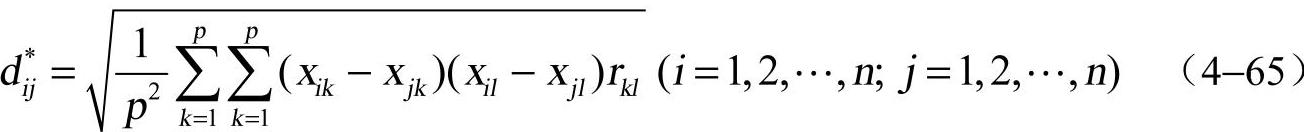
其中，r_kl是变量x_k和变量x_l之间的相关系数。

（2）相似系数

常用的相似系数有两种度量方法：

①夹角余弦。变量x_i和变量x_j的夹角余弦定义为

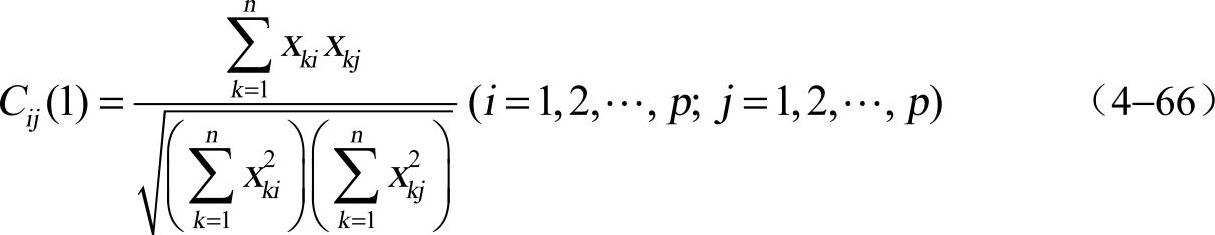
它是变量x_i的观测值向量（x_1i，x_2i，…，x_ni）′和变量x_j的观测值向量（x_1j，x_2j，…，x_nj）′间夹角的余弦值。

②相关系数。变量x_i和变量x_j的夹角相关系数为

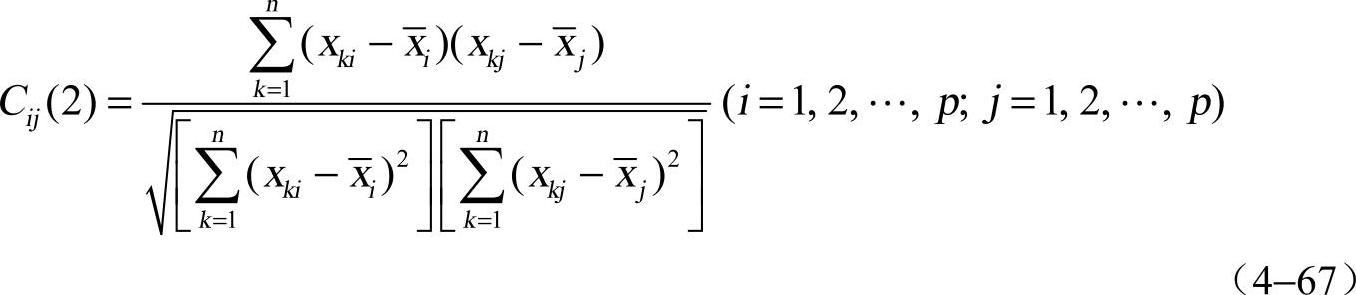
其中，

由相似系数还可以定义变量间距离，如

d_ij=1-C_ij（i=1，2，…，p；j=1，2，…，p）

3.聚类方法分类

聚类问题的研究已经有很长的历史。迄今为止，为了解决各领域的聚类应用，已经提出的聚类算法有近百种。根据聚类原理，可将聚类算法分为以下几种：划分聚类、层次聚类、基于密度的聚类、基于网格的聚类和基于模型的聚类。

虽然聚类的方法很多，但在实践中用得比较多的还是K-means、层次聚类、神经网络聚类、模糊C-均值聚类、高斯聚类这几种常用的方法。所以本节随后将重点介绍这几个方法。