新能源汽车大数据分析-多元线性回归分析

在一元线性回归分析中，假定因变量只受一个自变量的影响，然而研究许多现实问题时，研究对象往往受到多个自变量的影响，比如：公司股价可以由每股盈利、每股净资产等众多变量解释；作物产量受施肥量、浇水量、耕作深度等因素的影响；产品的销量不仅受销售价格的影响，还受消费者的收入水平、广告宣传费用、替代商品的价格等多个因素的影响。因此，研究一个因变量与多个自变量之间的数量关系需要用到多元线性回归分析。多元线性回归分析是指因变量表现为两个或两个以上自变量的线性组合关系，多元线性回归分析与一元线性回归分析的基本原理和方法类似。

1.多元线性回归模型

（1）多元线性回归的基本模型

多元线性回归模型与一元线性回归模型相似，只是自变量由一个增加到多个。设因变量y表现为k个自变量x₁，x₂，…，x_k的线性组合，则多元线性回归的基本模型可以表示为

在上述模型中，k为自变量的个数；β_j（j=0，1，2，…，k）为模型参数；ε_i表示随机误差项；（x_1i，x_2i，…，x_ki）为对总体的第i次观测。

与一元线性回归类似，多元线性回归方程为

在多元线性回归模型中，系数β_j表示在其他自变量不变时，第j个自变量变化一个单位对因变量均值的影响，又称偏回归系数。与一元线性回归模型一样，由于总体回归方程未知，只能利用样本进行估计，则样本回归方程和样本回归模型分别表示为

在上述模型和方程中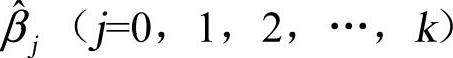，是总体回归参数β_j的估计。

（2）多元线性回归模型的矩阵表示

对于总体的n次观测，存在n个相同参数的回归方程组

将上述方程组用矩阵表达

Y=Xβ+ε （4-38）

其中，

样本回归模型和回归方程的矩阵表达为

其中，因变量均值向量、回归系数向量和残差向量分别为

（3）多元线性回归模型的假定

与一元线性回归模型相比，多元线性回归模型除了有随机项服从正态分布、随机项零均值、随机项同方差、随机项无自相关、随机项与自变量不相关的假定外，还假定各自变量之间不存在线性相关。

2.多元线性回归模型的参数估计

（1）多元线性回归参数的最小二乘估计

在一元线性回归参数的估计中，对于自变量和因变量的观测值可以借助二维平面坐标的散点表现。但在多元线性回归中，这些点不在一个平面上，需要借助多维空间的“点”描述。尽管如此，多元线性回归参数的估计原理与一元线性回归相同，也是采用残差平方和最小准则即普通最小二乘法估计模型参数。

对于一个包含n组观测值的样本（y_i，x_ji），其中i=1，2，3，…，n；j=1，2，3，…，k残差平方和为

使残差平方和最小的充分必要条件是：

由此得到k+1个求导方程：

将上述方程组简化，得到正规方程组

上述正规方程组为关于待估计参数的k+1元一次方程组，求解可得各待估参数的值。用矩阵表示参数的估计式为

（2）参数最小二乘估计的分布特征与性质

与一元线性回归一样，在满足经典假设的情况下，可以证明多元线性回归模型参数的最小二乘估计服从正态分布，并具有无偏性、最小方差性和线性。

（3）随机误差项的方差σ²的估计

在回归参数的方差和标准差公式中，σ²为总体回归模型中随机误差项ε_i的方差。σ²是无法观测得到的，但可以由样本回归模型中随机误差项进行估计，估计结果为(www.xing528.com)

可以证明，上述估计量是随机误差项ε_i的方差σ²的无偏估计。（n-k-1）是其自由度。

3.多元线性回归模型的拟合优度与统计检验

（1）多元线性回归模型的拟合优度

①多重可决系数R²。与一元线性回归类似，多元线性回归模型也需要考察模型对观测值的拟合程度，以说明模型的拟合优度。多元线性回归对模型拟合优度的考察，也是使用总离差平方和中回归平方和所占比重，即R²。与一元线性回归不同，多元线性回归的回归平方和是由多个自变量共同解释的部分。为了以示区别，将多元线性回归中回归平方和占总离差平方和的比重称为多重可决系数或复可决系数。R²的计算如下

或

R²的值越接近1，表明模型对样本数据的拟合程度越优。在实际应用中，R²达到多大才算模型通过了检验并没有绝对标准，应根据具体情况确定。值得注意的是，模型的拟合优度并不是判断模型质量的唯一标准，有时需要考虑模型的实际意义、回归系数的可靠性等因素。

②调整后的R²。在实际应用中发现，基于已经观测到的样本数据，如果在模型中增加自变量，则模型的解释功能增强了，残差平方和会相应减少，R²会增大。这就给人一个错觉：为了使模型拟合得更好，应增加自变量的个数。但在样本容量一定的前提下，增加自变量不仅会损失自由度，还会带来其他问题。为了消除自变量个数对模型拟合优度的影响，实际应用中往往对R²进行调整（Adjusted-R-Square），其计算公式为：

式中，（n-k-1）为残差平方和的自由度；（n-1）为总离差平方和的自由度。可以看出，R²经过调整比原来变小了。

（2）回归方程的显著性检验（F检验）

模型的拟合优度用于判断自变量对因变量的拟合程度。拟合优度越高，表明线性方程对数据拟合得越好，但这只是一个模糊的判断，需要给出统计上的检验。方程的显著性检验就是对模型的整体线性关系是否成立所进行的检验。方程的显著性检验使用的方法因构造的统计量不同而不同，其中以F检验应用最为普遍，一般的数据分析软件中都有F统计量的计算结果。

①检验的模型为

②要检验的假设为

H₀：β₁=β₂=…β_k=0

H₁：β_j（j=1，2，…，k）不全为0

如果H₀成立，则所有自变量系数全为0，表明由所有自变量构成的线性部分整体上不能解释因变量，即方程不成立；如果H₁成立，即至少有一个自变量系数不为0，则表明线性关系成立。

③检验的统计量。y_i服从正态分布，因此y_i的一组样本的平方和服从χ²分布，有

构造F统计量

在给定的显著性水平α下，如果F＞F_α（k，n-k-1），则拒绝H₀，即模型的线性关系显著成立，模型通过显著性检验；如果F＜F_α（k，n-k-1），则不拒绝H₀，表明回归方程中所有自变量联合起来对因变量的影响不显著，即模型的线性关系显著不成立，模型未通过显著性检验。

（3）变量的显著性检验（t检验）

在多元线性回归分析中，方程的总体线性关系成立并不能说明每个自变量对因变量的影响都是显著的，必须对每个自变量进行显著性检验。在一元线性回归分析中，因为只有一个自变量，所以方程的显著性检验等价于变量的显著性检验。多元线性回归中变量的显著性检验方法与一元线性回归相同，普遍使用t检验。

可以证明，回归系数的估计量服从正态分布

其中，参数的协方差矩阵为

以C_ii表示矩阵（X"X）^-1主对角线上的第i个元素；参数估计量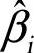的方差为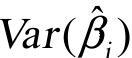为σ²C_ii

由于随机误差项ε_i的方差σ²未知，使用样本估计量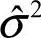代替，由此构造t统计量：

①构造假设为

如果拒绝H₀，则变量通过显著性检验，即自变量x_j对因变量y有显著的影响，否则自变量x_j对因变量y的影响不显著。

②计算t统计量的值。当H₀成立时，由样本数据计算出检验的统计量为

③依据临界值进行检验。给定显著性水平α，得到临界值t_α/2（n-k-1），如果|t|＞t_α/2（n-k-1），则拒绝H₀，变量通过显著性检验，即变量x_j对因变量y有显著的影响，否则不能通过显著性检验。