1)降雨补给与计算水头
城市隧道应将大气降雨作为重要的地下水补给考虑到隧道水问题的计算中,但对地下水位造成影响的不仅是降雨量,还有地下水损失,其损失量主要表现为地表径流、河川径流及蒸发量。由于径流及蒸发量的分析较为复杂,与降雨量、前期地表储存、截留、土壤下渗能力、前期土壤水分等条件有关。因此,计算时可采用美国水土保持局(SCS)提出的曲线数值法估算[186],即
式中,hs为损失量;p为降雨量(一般取汛期平均降雨量);Ia为初始拦截量,通常为0.2S;CN是由经验确定的数值(见表6.1),与土壤下渗能力、土地利用状况、前期水分条件有关。
根据地质勘探资料可知,隧址区初始水头高度h,考虑降雨、蒸发量及其他径流损失后,就可得到实际计算水头h0为
式中,h0为计算水头;h为初始水头(是指地下水位线至隧道中心的距离)。
表6.1 CN经验取值
2)围岩平均渗透系数
根据水力学渗透理论,隧道排水可简化为一个降落漏斗模型(见图6.2),从隧道边界取一“竖条地层”,将其抽离该模型。由于在“竖条地层”中除隧道排水外没有其他排水途径,故从两侧流入该“竖条地层”(即假想降水井)的水量等于隧道排水量。
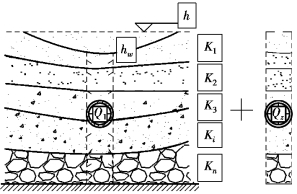
图6.2 隧道涌水降落漏斗模型
对均质各向同性且底部为水平潜水含水层的围岩,若含水层上部有均匀入渗、排水稳定的隧道,潜水流即可视为稳定流[165]。应用裘布依假定,将隧道看成稳定井,假想降水井包含多种地质条件的地层,则每一层均可单独视为稳定流,故每一层均可应用裘布依水井理论。因各含水层因水井排水导致的水头损失相同,故其对水井提供的流量为[164]
式中,Qi为某含水层的水井排水量;Sw为水头降落高度;Ki为某含水层渗透系数;Mi为某含水层厚度;r为隧道半径;R为降水影响半径。
因此,整个水井的排水量为
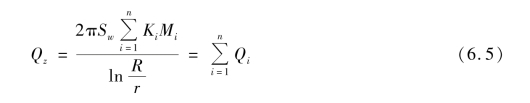
式中,Qz为假想水井的排水量。
现假定隧道所在地层为单一地层,该地层渗透系数为
,则
式中,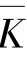
为围岩平均渗透系数;h为假想水井的初始水头高度,即初始水位线到假想水井井底的距离;hw为假想水井水位降落后高度,高水位隧道中h=2h0;hw+Sw=h。
由式(6.5)和式(6.6)可得
3)高水位城市隧道排水量与水压力研究
控制型防排水隧道由内向外的防排水构造为二衬、防水层、排水管、初衬和注浆圈。初衬和注浆圈的作用是减少进入隧道的总水量,防水层和二衬起到主要的隔水作用,而排水管是为了引流渗入初衬的地下水,避免其聚集于二衬外壁,以减少水压力。因此,隧道防排水设计的思路便是研究水压力和排水量之间的关系,寻求二者间的平衡点。
完全按隧道实际状况对隧道排水量和水压力研究较为困难,实际排水量受排水管形式、直径和间距等的影响难以定量描述,需进行必要的简化。假定地下水会渗入隧道内壁,此时,内壁处的水头决定排水量的大小,改变其水头即可模拟不同的防排水形式,进而利用求出的内壁渗水量代替实际隧道排水量。为方便求解,同时满足隧道排水量与水压力预判的合理性,还做了以下简化:
①隧道断面为圆形,沿轴线水平分布。
②将围岩视为各向同性介质,可用围岩平均渗透系数计算。
③渗流达到稳定状态,不随时间变化。
④地下水渗流满足达西定律和渗流连续性方程。
简化后的高水位隧道计算模型如图6.3所示。其中,隧道内壁半径为r,二衬外半径为R1,初砌外半径为R2,二衬渗透系数为K1,初衬渗透系数为K2,注浆圈半径为Rg,注浆圈渗透系数为Kg,围岩渗透系数为Kr。
隧道排水量预测时,仅截取某断面上单位长度进行计算(见图6.3),即简化为平面渗流模型,则拉普拉斯方程可写为
边界条件是渗流场问题有定解的必要条件,本研究涉及两类定值边界条件。
第一类为外边界条件,是指模型外部应满足的边界条件,由实际外边界简化而来。当模型中没有除隧道外的排水途径时,开挖前后的外边界如图6.3所示。开挖后地下水向隧道汇集,引起隧道周围地下水位下降,水头随位置而变化,且离隧道越远受到的影响越小,趋近于隧道开挖前,则有
而实际情况下的模型外部边界(水位线)为一条难以描述的曲线,模型远场边界也难以应
用。为此,引入外边界条件为[128]
图6.3 高水位隧道计算模型
式(6.10)的物理意义为:距隧道中心达Rr时,隧道排水对该处水头的影响可忽略不计,选用圆形边界是为了与隧道断面吻合,方便求解。为使计算准确,应尽量增大Rr的值,使边界远离隧道但不超过地下水位线,即高水位隧道渗流影响范围为Rr=h0。
第二类为内边界条件,是指隧道内壁处应满足的边界,即
式中,ha为隧道中心内壁水头;yc为隧道内壁纵坐标值(坐标系见图6.3)。
式(6.11)表示在隧道内壁处只考虑位置水头,而忽略了压力水头,且内壁最大水头差在拱顶和拱底处,差值为2r。当r≤h0时,隧道内壁处的水头差可忽略不计,即
现利用拉普拉斯方程和上述边界条件求解水头函数Φ(x,y),式(6.8)在极坐标(ρ,θ)下可表达为
(www.xing528.com)
由于两类边界条件均为水头恒定的圆弧,对过原点的任意轴线,该模型均轴对称,故可认为水头函数只与某点到隧道中心的距离有关,而与该点到隧道中心的极角无关,即
。因此,式(6.13)简化为
由式(5.14)易得
式中,B,C为待定常数。
由式(5.15)可得
除前述两类边界条件外,隧道渗流场还应满足水头[见式(6.17)]及流速[见式(6.18)]连续边界条件,包括围岩、注浆圈、衬砌等的接触边界。其中,流速可通过达西定律转化为水头的微分,即
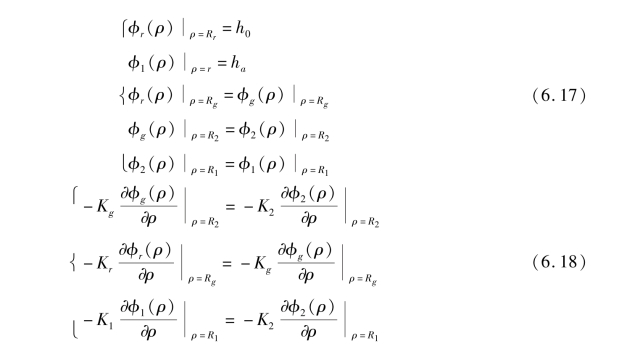
将式(6.17)和式(6.18)代入式(6.16)中,可得
此时,渗入隧道内流量Q为
由达西定律和式(6.16)可得
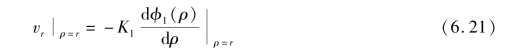
将式(6.19)和式(6.21)代入式(6.20),得
联立式(6.3)、式(6.7)和式(6.22),并结合高水位隧道渗流影响范围可得
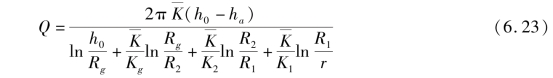
根据前述假定,地下水可渗入隧道内壁,则内壁压力水头为0,因此,隧道中心内壁水头ha=0。将式(6.19)代入式(6.16)后,可得二衬背后的水压力为
考虑高水位隧道yc≤h0,故可忽略yc对二衬外水压力的影响,即
4)低水位城市隧道排水量与水压力研究
地下水位较低的城市隧道,其排水量和二衬外水压力的计算与高水位相比存在较大差异,主要由于距地表较近,隧道排水对上部围岩的渗流影响与其他方向不同。此时,高水位理论的边界条件已不再适用,有必要对低水位隧道排水量和二衬外水压力进行深入研究。计算中,降雨补给和计算水头的分析见6.1节所述理论,围岩平均渗透系数仍采用式(6.7)计算。其中,低水位隧道h=h0+R,R为假想水井降水影响半径[即式(6.28)中的R]。
为方便研究低水位隧道的排水量和水压力,采用与前述高水位隧道相同的简化,简化后的隧道计算模型如图6.4所示。其中,隧道半径为r,隧道埋深为c,围岩平均渗透系数为K。
图6.4 低水位隧道计算模型
低水位隧道仍涉及两类边界条件:第一类为外边界条件,将实际情况下的外部边界(地下水位曲线)视为一条直线,即
第二类为内边界条件,与高水位情况相比存在较大区别,高水位隧道内壁y坐标的变化对水头影响较小,可视为内壁上等水头,而地下水位较低时,隧道内壁水头随y坐标变化明显,即其内壁水头为
式中,yc为隧道内壁的位置水头,-r≤yc≤r。
由复变函数保角映射理论、二维稳态流动的复变函数理论和低水位隧道边界条件,可解得低水位隧道地下水渗流场的水头表达式为[176,187]
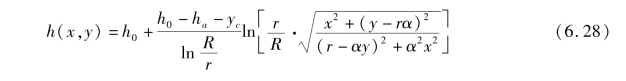
式中,。
因低水位隧道内边界上等水压线的存在,其切向流速不等于零,引入以隧道中心为原点的极坐标(ρ,θ),故沿外法线方向的流速为
此时,渗入隧道的流量为
联立式(6.3)、式(6.7)、式(6.29)、式(6.30),可求得低水位隧道毛洞状态下的排水量为
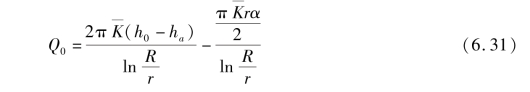
由于轴对称解析在低水位隧道水压力及排水量折减计算中仍然适用[188-189],因此,与前述毛洞状态相比,排水量折减系数为
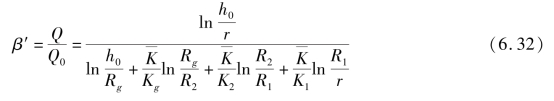
水压力折减系数为
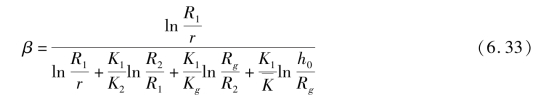
因此,考虑注浆圈、初衬和二衬的折减效应后,低水位隧道排水量为
低水位隧道二衬外水压力为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
