地下水渗流数值模拟成果

工程实际中的水文地质条件往往较复杂:地形起伏多变,岩层不连续且时空分布不均,岩性差异大,含水层厚度不均一,非均质,各向异性,水文地质参数的时空变异性明显等。数值模型能对上述特点做到相对合理地表述,可尽量真实地还原地下水渗流场。

目前数值模拟方法很多,主要包括有限差分法(FDM)、有限单元法(FEM)、边界元法(BEM)及有限分析法(FAM)等[143]。随着计算机技术的发展,尤其近十几年,地下水系统数值模拟进步明显,并已发展为由二维模型转变为三维模型[144]。据地下水系统数值模拟的研究现状和发展趋势统计,多款地下水数值模拟软件在实际工程应用中取得了良好的效果[145],尤其以Visual-modflow的模块化、可视化、交互性、求解方法多样化等优势功能得到广泛的使用,几乎占到了地下水数值模拟应用的一半以上。随着时间推移,Visual-modflow功能已有了很大改善,操作更加人性化,提供了完善的输入、修改、分析和显示地下水模型的平台[146-148]。

利用数值软件分析地下水渗流问题遵循地下水渗流力学的一些基本理论,作为流体力学的一部分,其主要针对多孔介质进行研究[149]。地下水渗流运动需要同时满足质量守恒定律和能量守恒定律,质量守恒定律是俄国科学家罗蒙诺索夫于1756年最早发现的,拉瓦锡通过大量的定量试验,发现了在化学反应中,参加反应的各物质质量总和等于反应后生成各物质的质量总和。它是自然界普遍存在的基本定理之一,在地下渗流研究领域,质量守恒定律被诠释为区域水均衡原理。能量守恒定律即热力学第一定律,是指在一个封闭(孤立)系统的总能量保持不变。一般来说,总能量已不再只是动能与势能之和,而是静止能量(固有能量)、动能、势能三者的总量,其在地下渗流研究领域表现为达西定律。

地下水研究领域中的水均衡原理是指在一定的区域内,使区域内地下水总量增加(如降水垂直入渗量、上游断面流入量、注水回灌等)与减少(蒸发量、下游断面流出量、钻井抽水等)的总和等于区域内原有的地下水储存总量的变化量。在一般情况下,由于天然的环境下温度变化幅度有限,因此,水的体积受温度影响较小,通常也可用流体的体积来近似代替质量[150]。

达西定律由法国水力学家H.-P.-G.达西在1852—1855年通过大量实验得出,后来推广应用于其他土体如黏土和具有细裂隙的岩石等。达西定律广泛适用于水头损失与流速的一次方成正比、流速与水力梯度呈线性变化等的层流领域,而在流速与水力梯度呈非线性变化的紊流条件下则不再适用。用总水头表示在地下水运动场中某一点总能量大小为[151-152]

式中,H为总水头;p为该点处的静水压力;γ为水的重度;u为地下水的流速;g为重力加速度;z代表该点相对于参考位置的高度也是位置水头;为压力水头;z+统称为测压管水头;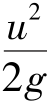为速度水头。(www.xing528.com)

不考虑水头损失,则总水头为一个常数,而通常地下水渗流的速度较小,速度水头又是渗流速度的二次项,因此,可忽略速度水头,从而得到

同时,考虑水具有粘滞性,尤其可能含有丰富的可溶物或电解质等杂质,在地下渗流过程中容易产生摩擦阻力。总能量在摩擦阻力作用下减少,而达西定律论证得到水头损失和渗透速度以及渗流路径长度成正比,在一维渗流路径取微元时,得到达西定律的微分形式为

式中,q为渗透速度,即单位面积每秒流量;K为渗透系数。

式(4.11)具有较为普遍的一般形式,当含水层各向异性,渗透性质差异较大时,可将上式推广为三维流

式中,qx,qy,qz分别为x,y,z方向上的流速分量。