模型试验相似理论探究

模型试验应遵循一定的相似规律,试验中涉及的n个物理量包含k个相互独立的基本因次,而这个物理过程可由n-k个无因次量所表达的关系来描述,这符合相似第二定理的特征[125-127]。

假设某一现象的自变量和因变量可由方程组表示为

经过第二种相似变换,可将式(4.1)转化为无因次的相似准则π1,π1,…,πn-k之间的函数关系,即

式中,π1,π1,…,πn-k均为相似准则,它们以乘因子的形式出现,且有n-k个。以后将式(4.2)称为准则关系式或π关系式,也将相似第二定理称为π定理。

对彼此相似的现象,在对应点和对应时刻上相似准则都保持同值。因此,它们的π关系式也应当是相同的,对原型(p)和模型(m)分别为

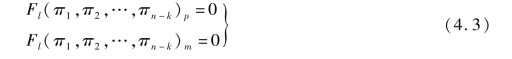
其中,必有(www.xing528.com)

针对本矿山法城市隧道渗流试验,研究核心是以地下水渗流理论为出发点的隧道渗流及防排水等问题,其水压力和排(涌)水量值主要与隧道洞径、作用水头、渗流影响半径以及围岩-支护体系的渗透系数等参数相关,而与围岩、注浆圈、初衬等材料的物理力学特性关联不大[113,128]。因此,忽略围岩-支护体系的物理力学特性和变形稳定性[129],以控制相似材料的渗透系数为核心,认为二衬为不透水结构,渗进初衬的水通过二衬背后的排水系统导出并收集,主要研究隧道排(涌)水量Q、水压力P等。

渗透是液体在多孔介质中运动的现象,而渗透系数是表达介质渗透能力的定量指标,故选定以渗透系数相似比CK、几何相似比CL和重度相似比Cγ为基础相似比。本次隧道渗流模型试验中,选定几何相似比CL=1/30,渗透系数相似比CK=1,重度相似比Cγ=1。

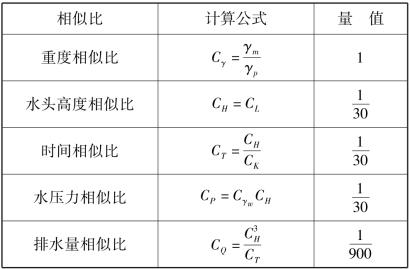
因此,以相似第二定理为理论基础,采用量纲分析法推导出相似关系[130-131],见表4.1。

表4.1　渗流试验相似关系表

续表