月球运动-天文学教程 上册

月球是离地球最近的天体。古代人用月球的运动周期变化来计量时间，从而对月球的运动进行了大量研究。影响月球运动的因素很多，其中最主要的是地球和太阳的引力。

1）月球绕地球的轨道

月球绕地球做轨道运动，同时又随着地球绕太阳公转。月球在天球上相对于众恒星的视运动很显著。月球绕地球转动的轨道面交于天球的大圆，即月球在天球上的视运动轨迹，称为白道。月球绕地球转动轨道是半长径为384400 km、偏心率为0.0549的椭圆，月地距离在356400 km（过近地点时）到406700 km（过远地点时）之间变化，白道与黄道交角为5.145°，与地球赤道面交角变化为18.29°～28.58°（见图3-22）。

由于太阳和其他行星的引力摄动等影响，月球轨道发生复杂的变化（见图3-23）。

图3-22　月球绕地球轨道和地月系绕太阳公转运动

图3-23　月球轨道的变化

月球轨道半长径大约以每年3.52 cm的速率在增大，逆推它在12亿年前离地球仅18000 km；轨道偏心率变化范围为；白道与黄道的交角以173天的周期变化±9′；月球轨道“拱线”（即近地点与远地点连线）向东进动，8.849年进动一圈；白道与黄道的升交点西移，18.61年转过一圈。

按不同的基准来计量，月球的轨道运动周期有以下几种：

（1）恒星月是以恒星为基准，月球沿白道视运动一圈，实际上是月球绕地球转动一圈的时间间隔，1恒星月为27.321661 d（平太阳日）；

（2）近点月是月球连续两次经过近地点的时间间隔，1近点月为27.55455 d；

（3）交点月是月球连续两次经过升交点的时间间隔，1交点月为27.21222 d；

（4）朔望月是月相变化的周期，它是以太阳为基准的会合运动周期，月球与太阳的地心黄经连续两次相同（朔）或相差180°（望）的时间间隔，1朔望月为29.530589 d。

一般按照需要来选用“月”周期，例如，日常生活常用的农历（阴历）“月”是朔望月；地震发生周期与近点月有关。

由于月球绕地球转动的同时还和地球一起绕太阳公转，因而月球在天球上相对于太阳的视运动是一种会合运动（见图3-24）。在“朔”时，月球M和太阳S的地心黄经相同。经过一个恒星月，地球和月球运行到E1和M1处，月球的地心黄经又达同样值，E1M1平行于EM，但月球还需要再运行一段时间才达到太阳S与地球E1之间而与太阳的地心黄经相同——下次朔，因而朔望月比恒星月长。

以T表示恒星月、S表示朔望月，E表示恒星年，则不难导出会合方程式：

图3-24　地球和月球与太阳的会合运动

2）月相和月龄

苏东坡写了脍炙人口的词句“月有阴晴圆缺，此事古难全”，它表述的就是月相不以人的意愿而客观地周期变化。月相周期变化的原因有二：一是月球、地球和太阳的周期性会合运动，它们的相对位置呈现周期性变化；二是月球本身不发射可见光，而我们看到的只是月球被太阳照亮的部分。(www.xing528.com)

在月球、地球和太阳的周期性会合运动中（见图3-25），当月球运行到地球与太阳之间、月球与太阳的地心黄经相同之时（定为农历月的初一），当天月球与太阳几乎同时从东方升起，又几乎同时从西方落下，由于月球未被太阳光照的暗半球对向地球，“视而不见”，这称为朔月或新月。随后，月球与太阳的黄经之差逐渐增大，向东偏离太阳，日落后在西方看到月球被太阳照亮的小部分呈弯向西的镰刀形“娥眉月”。当月球与太阳的黄经之差达90°时，我们看到月球被太阳照亮半球的一半而呈半圆形，称为上弦月。其后，我们看到月球被太阳照亮的部分更多的“凸月”。到月球与太阳的黄经之差达180°（农历每月十五或十六）时，我们可以看到月球被太阳照亮的全部半球呈圆形，成为满月或望。望之后，我们看到月球被太阳照亮的部分逐渐减少的“凸月”。当月球与太阳的黄经之差达270°时，我们看到被太阳照亮的月球另半球而呈半圆形，称为下弦月，而后在黎明前看到呈弯向东的镰刀形“残月”。经过一个朔望月，又开始下次新月和重复的月相变化。

图3-25　月球的会合运动与月相变化

虽然在月相变化中，我们看到的只是月球被太阳照亮的部分，月球没有被太阳照亮的其余部分也不是完全黑暗的，而是被地球大气反射或散射的太阳光照到，仍依稀有“灰光”，尤其用强光力望远镜可以观测到月球的灰光部分。月球的灰光是由于地球反射少量太阳光照到了月球背太阳的部分。

3）月球的同步自转

月球绕地球转动的同时还在自转，月球自转轴与白道面法线交角为6.687°，自转方向与绕地球的轨道运动方向相同，自转周期等于恒星月，这称为“同步自转”。白道面与黄道面保持着5.145°的夹角，因而月球自转轴与黄道面的法线成1.542°的夹角，导致月球基本上总以一侧对着地球，从地球上看到的只是月球的“正面”，而看不到“背面”，如图3-26所示。

可以用图3-27说明同步自转，图平面为月球轨道面，大圆表示月球轨道。当月球在轨道上M1时，地球上看到月球上的a点正位于视面中心；当月球沿轨道绕地球转圈到达M2时，月球自转周，因而月球上的a点仍在视面中心；类似地，当月球绕地球转圈到达M3时，月球自转周；当月球绕地球转圈到达M4时，月球自转周，a点都在视面中心。

图3-26　地球-月球系统的自转及轨道面的相对关系

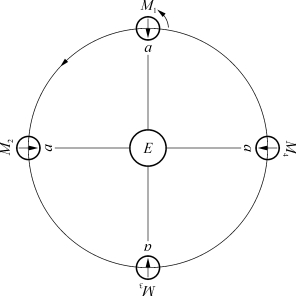
图3-27　月球的同步自转

确切地说，“月球总以一侧对着地球”这句话只是近似的。实际上，由于月球自转轴并不完全垂直于白道面，月球沿其椭圆轨道运动不均匀而发生“摆动”，我们有时可以看到月球背面边缘部分，因而能够看到月球表面总面积的59%。这种现象称为天平动，根据成因而分为光学天平动和物理天平动。

光学天平动是因月球相对于地球的位置变化所致，又称为几何天平动或视天平动，有如下三种。

（1）经（度）天平动　由于月球绕地球运动的轨道是椭圆，轨道运动速度不均匀，从处于其轨道焦点的地球上看，不同时间垂直视向的月面经度范围有差别，如图3-28所示。当月球过近地点M1时，轨道速度最快；过远地点M3时，速度最慢；由于月球自转，其表面b点总是对向轨道中心O。当月球在M1时，b点对向地球E的视向，地球上看见月球的abc半球；月球运动到M2时，其自转恰经轨道周期P的，b点还未自转到视向，地球上看见月球c点后面的小部分（图上最暗）明显的“露出”；月球运动到M3时，其b点又自转到视向；然后，反向摆动；月球运动到M4时，地球上却看见月球a点后面的小部分明显的“露出”。月球可见表面的这种变化表现为经度方向的摆动，故谓之经（度）天平动，平均摆动可达7°54′，摆动周期为近点月。

图3-28　月球的经天平动

（2）纬（度）天平动　由于月球的赤道面与白道面平均有6.41°的交角，而自转轴的指向几乎不变，所以月球轨道运动到不同位置，地球上看到月球表面有纬度范围的摆动，如图3-29所示。当月球运动到M1时，地球E看见月球的近南极区；而到M2时，则看见月球的近北极区。这种可见月球表面的纬度摆动谓之纬（度）天平动，显然，在月球轨道运动到其赤白交点时不见这种摆动，而与交点角距90°时（图中M1，M2）纬天平动幅度最大，摆动周期为交点月。

图3-29　月球的纬天平动

（3）周日天平动　由于月球离地球较近，地面上不同经纬度或不同时间观测到的月球表面因视差而有些差别，谓之周日天平动或视差天平动，其幅度较小，仅约1°。

物理天平动是由于月球不是理想的球体，物质分布不均匀，其几何指向与质量中心偏离，加上受地球的引力摄动，月球本身在空间绕其质量中心的晃动表现为月球自转轴的空间指向和自转速率的微小变化，幅度约为2′，当代精密的月球激光测量需要改正其影响。