测定月球距离方法-天文学教程 上册

公元前3世纪，古希腊的阿利斯塔克（Aristarchus）曾测量月球M在上、下弦时与太阳S的角距∠MES（△MES为直角三角形，见图3-19左），虽然其测量误差很大，但证明了月球比太阳近得多。约一个世纪后，伊巴谷由两地观测同一次日食，算出地月距离为地球半径的59～67.3倍。

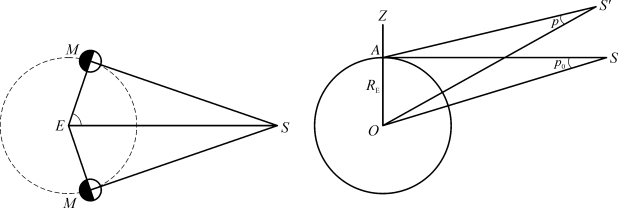
图3-19　月球上、下弦与太阳的角距（左）以及天体的周日视差（右）

直到18世纪中期，人们才采用周日视差法测出月球距离。其原理与地面上的三角测距法一样：以地球半径RE为基线的OA与天体S′组成的△AOS′中，端点A、O到S′视线的交角p（即∠AS′O）称为视差（见图3-19右）。由于p值随天体的周日视运动而变化，故称为周日视差。当天体恰在点A的天顶时，p=0°。当天体S处于地平面时，其视差p0最大，称为地平视差，显然，△OAS为直角三角形，天体S到地心距离D=OS为

于是，地月距离的测定转移为测定其地平视差p0。最简单的方法是在同一子午圈上、地理纬度φ1和φ2的两点A、B观测月球的视赤纬δ1和δ2，以点A为例（见图3-20），月球对A的天顶距为z1，对地心的天顶距为z，在△AME中，由角关系和正弦定理得

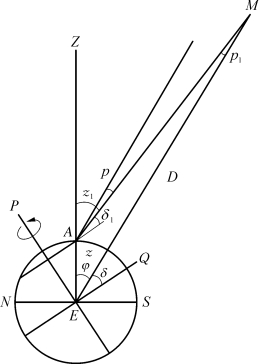
图3-20　地月距离测定(www.xing528.com)

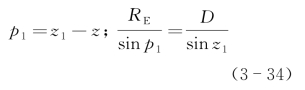
将式（3-33）代入式（3-34），可得

相减可得

用式（3-34）及z1=φ1-δ1和z2=φ2-δ2，并考虑到下角近似sin（δ-δ1）≈δ-δ1（弧度数），就得到

自1957年以来，科学家先后用雷达和激光测距法测定地月距离。其原理很简单：测量从信号发射到月面反射回来的时间间隔Δt，则距离d=cΔt／2（c是光速）。虽然激光测距可准确到±8 cm，但还需进行信号发射点与地心距离和月面反射点与月心距离，以及月球轨道椭圆的有关改正。现在采用的地月距离平均值为384401 km。